4.4 A supermassive black hole

A black hole is a body so massive and so small that even electromagnetic radiation, such as visible light, cannot escape from it. It is its combination of small size and very strong gravitational field that makes it attractive as a key component of the engine that powers an AGN. There is good evidence of a black hole of mass 2.6 × 10⁶M_⊙ at the centre of the Milky Way. As you will see, it turns out that much more massive black holes are needed to explain AGNs, and these are referred to as supermassive black holes.

A black hole, supermassive or otherwise, is such a bizarre concept that it is worth recapping. The material of which it is made is contained in a radius so small that the gravity at its 'surface', the so-called event horizon, causes the escape speed to exceed the speed of light. According to classical physics, any object that falls into it can never get out again. Even electromagnetic radiation cannot escape, which is why the hole is called 'black'. What goes on inside the black hole is academic - no one can see. What might be seen is activity just outside the event horizon where the gravitational field is strong, but not so strong as to prevent the escape of electromagnetic radiation. It is this surrounding region that is of most interest to astronomers.

The radius of the event horizon is called the Schwarzschild radius and is the distance at which the escape speed is just equal to the speed of light. It is given by

Let us now calculate the maximum mass M of a black hole that is small enough to fit inside an AGN. In Section 4.2 you found that an AGN that varies on a timescale of one day must have a radius less than 3 × 10¹² m. We shall see later that all of the emission from the AGN must come from a region that is outside of the Schwarzschild radius and that the size of this emission region is a few times bigger than R_S. Consequently, for this approximate calculation we shall adopt a size for R_S that is a factor of ten smaller than the size we calculated above for the emission region, i.e. R_S = 3 × 10¹¹ m. Then, from Equation 3.4,

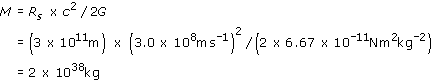
which is equivalent to

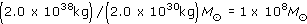
This result shows that is clearly possible to fit a black hole with an enormous mass within an AGN, although it does not prove that the central black hole has to be this massive. We will shortly see that there is a different argument that does show that mass of any black hole at the centre of an AGN must be about 10⁸M_⊙. This is usually adopted as the 'standard' black hole mass in an AGN. It is some 10⁷ times greater than the masses of the black holes inferred to exist in some binary stars that emit X-rays. Hence, the name supermassive black hole has been adopted.