4.6 Accretion power

Calculations based on the above accretion disc hypothesis show that if a mass m falls into the black hole, then the amount of energy it can radiate before it finally disappears is about 0.1 mc², or about 10% of its rest energy. Other than matter-antimatter annihilation, this is the most efficient process for converting mass into energy ever conceived. A comparable figure for the nuclear fusion of hydrogen in stars is only 0.7% of the rest energy of the four hydrogen nuclei that form the helium nucleus.

Question 9

How much energy could be obtained from 1 kg of hydrogen (a) if it were to undergo nuclear fusion in the interior of a star, (b) if it were to spiral into a black hole? Would you expect to get more energy if it were to chemically burn in an oxygen atmosphere?

Answer

A mass m has a rest energy of mc².

(a) If 1 kg of hydrogen were to undergo nuclear fusion to produce helium, the energy liberated would be 0.007 (i.e. 0.7%) of its rest energy:

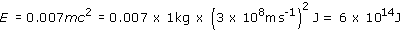
(b) If 1 kg of hydrogen were to fall into a black hole, the energy liberated would be approximately

0.1mc² = 0.1 × 1 × (3 × 10⁸ms⁻¹)² J = 9 × 10¹⁵ J.

You would expect much less energy from the chemical reaction.

Now let us apply the idea of an accreting massive black hole to explain the luminosity of an AGN. We have to explain an object of small size and large luminosity. The Schwarzschild radius of a black hole is very small, and the part of the accretion disc that radiates most of the energy will be only a few times this size. The luminosity will depend on the rate at which matter falls in. Suppose that the matter is falling in at the rate Q (with units of kg s⁻¹), this is known as the mass accretion rate. We can now work out the value of Q to produce a luminosity L by writing

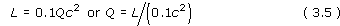
Using the values L = 10³⁸ W and c = 3 × 10⁸ m s⁻¹, we get Q = 10²² kg s⁻¹. Converting this into solar masses per year using 1M_⊙ ≈ 2 × 10³⁰ kg and 1 year ≈ 3 × 10⁷ s, we get Q ≈ 0.2M_⊙ per year. Is there a large enough supply of matter for a fraction of a solar mass to be accreted every year? Most astronomers think that the answer is yes, and that even higher accretion rates are plausible - after all our own Galaxy has 10% of its baryonic mass in gaseous form, so there is at least 10¹⁰M_⊙ of gas available.

• Does this estimate of the accretion rate require a supermassive black hole, or will any black hole such as one of 5M_⊙ do?

• The mass of the black hole does not enter into the above calculation. So on this basis a 5M_⊙ black hole would seem to be sufficient.

Moreover, the mass calculated in Section 4.4 is an upper limit. So, why is a supermassive black hole needed? To see why, we ask: is there any limit to the power L that can be radiated by an accretion disc around a black hole, or can one conceive of an ever-increasing value of L if there is enough matter to increase Q?

There is a limit to the amount of power that can be produced, and it is called the Eddington limit. As the black hole accretes faster and faster, the luminosity L will go up in proportion, that is to say the accretion disc will get brighter and hotter. Light and other forms of electromagnetic radiation exert a pressure, called radiation pressure, on any material they encounter. (This pressure is difficult to observe on Earth because it is difficult to find a bright enough light source.)

Around an accreting black hole with a luminosity of 10³⁸ W, the radiation will be so intense that it will exert a large outward pressure on the infalling material. If the force on the gas due to radiation pressure exactly counteracts the gravitational force, accretion will cease. This process acts to regulate the luminosity of an accreting black hole.

To work out the Eddington limit, it is necessary to balance radiation pressure against the effects of the black hole's gravity. Consider an atom of gas near the outer edge of the accretion disc. The force on it due to radiation pressure is proportional to L, whereas the gravitational force is proportional to the mass M of the black hole (assuming the mass of the accretion disc to be negligible). A balance is achieved when L_E = constant × M, where L_E is the Eddington limit. Full calculations give

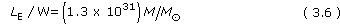
This is the upper limit of the luminosity of a black hole of mass M - the luminosity can be lower than L_E but not higher. The larger the mass M, the greater the value of L_E.

In fact, this is only a rough estimate. It assumes that the accreting material is ionized hydrogen (a good assumption) and that the hole is accreting uniformly from all directions (which is not a good assumption). The Eddington luminosity may be exceeded, for example, if accretion occurs primarily from one direction and the resulting radiation emerges in a different direction. Nonetheless, it is a useful approximation.

Putting L = 10³⁸ W into Equation 3.6, we find that M= 7.7 × 10⁶M_⊙. So we see that we do need a supermassive black hole to account for the engine in an AGN, and 10⁸M_⊙ is usually assumed.

In summary, then, the Eddington limit means that the observed luminosity of quasars requires an accreting supermassive black hole with a mass of order 10⁸M_⊙; the accretion rate is at least a significant fraction of a solar mass per year; and the Schwarzschild radius is about 3 × 10¹¹ m.