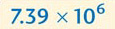2.4 Scientific notation

To express a number in scientific notation the first stage is to divide it successively by 10 until it is reduced to a number that is less than 10. For example, to express the number 4865 in scientific notation I would divide it successively by 10 until I arrived at 4.865. Usually this will result in a number that includes a decimal fraction (the number that follows the decimal point) as well as a whole number part. In my example, 4 is the whole number part and .865 the decimal fraction.

The next stage is to give some indication of how many times the number would have to be multiplied by 10 in order to return it to its original value. In my example I made three successive divisions by 10, so I would have to multiply by 10 three times – that is 10×10×10 – to return to the original value. So my number could be expressed as 4.865×10×10×10, but this is hardly a shorthand alternative. So instead of writing 10×10×10, I can express this as 10³. The first figure (10 in this case) is known as the base and the second figure (3 in this case) is known as the power or exponent (or sometimes the index). The example would be read as 'ten to the power of three'.

The final stage in scientific notation is to join together the results from the two earlier stages using a multiplication sign giving, in my example, 4.865×10³.

Any number can be expressed in scientific notation. For example:

Show description|Hide description

This is an equation, which reads five thousand equals five times ten, times ten, times ten equals five times ten to the power of 3.

Show description|Hide description

This is an equation, which reads seventy-two thousand equals seven point two times ten, times ten, times ten, times ten equals seven point 2 times ten to the power of four.

Show description|Hide description

This is an equation, which reads eighty-two thousand, six hundred equals eight point two six times 10, times ten, times ten, times ten equals eight point two six times ten to the power of four.

Fortunately, there is a quicker way of doing the conversions than by writing out all of the multiplication stages. I'll use the number 7 390 000 to demonstrate the method. Start by imagining there is a decimal point at the right hand end of the number. (I'll add a final 0 so that the decimal point can be seen clearly. This extra 0 is redundant since it doesn't alter the original value at all.)

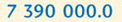
Now move the decimal point one place at a time until it sits after the left-most number, and count the number of places the decimal point has been moved:

Show description|Hide description

This image shows the figure seven point three nine zero, then three more zeros, then one more zero. Curved lines with arrows above the figures, from right to left, show how the decimal point has moved 6 places to the left.

(decimal point moved 6 places to the left)

Now remove all the Os at the right-hand end after the decimal point (because these are redundant) and multiply what is left by 10 raised to the power of the number of places the decimal point has been moved.

Show description|Hide description

This image shows the equation seven point three nine times 10 to the power of six.

You will often see a number expressed just as the base and the power – for example 10⁶ and 10². This is interpreted as 1×10⁶(=1 000 000) and 1×10² (=100).

In the answer to Activity 8, notice how the answer to (4) is expressed in base and power notation as 6.9×10¹ – meaning 'multiply 6.9 by 10 once'. Of course this gives exactly the same result as 6.9×10 and it is just as acceptable to omit the index in cases like these. In fact, it is normal to do so. However we have left it in because we want you to be aware that 10¹ is simply an alternative way of writing 10. Probably you are now wondering why anyone would want to bother with this, since the 'shorthand' ends up longer than the 'longhand' version. For now, just take our word for it that this method of expressing numbers will allow you to perform some arithmetical 'tricks' that can help to simplify some calculations.