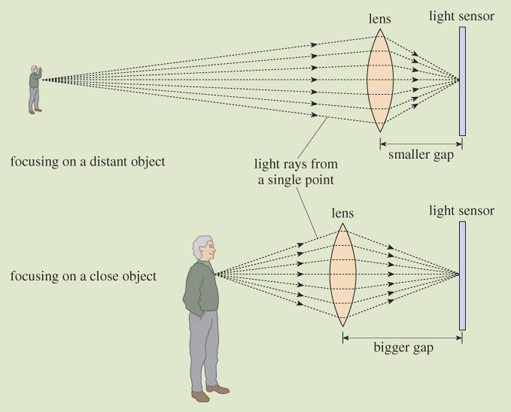
4.2.5 Focusing

Focusing is done by adjusting the size of the gap between the lens and the light sensor. To get distant objects in focus, the gap needs to be smaller than that required for close objects (see Figure 7 below).

Maximise

Figure 7 Focusing light using a camera lens

In theory the exact gap size is determined by the exact distance to the object being filmed. In practice, one gap size will be adequate for a range of object distances, this range being called the 'depth of field'.

Focusing in a camcorder is invariably done with an electric motor moving a lens, and there will be a facility to focus automatically (autofocus). Auto focusing is either passive or active.

Passive autofocusing works by a computer embedded in the camera examining the image (from the light sensor) to determine whether it is in focus or not.

Under control of the camera's computer, the motor will move the lens in and out to find the best focus, identified by the presence of sharp lines in the image.

Active autofocusing works by the camera measuring the distance to the object viewed, and using that to calculate the gap needed between lens and light sensor. It measures the distance by sending out pulses of infrared light towards the object being filmed, and measuring how long it takes the reflected light to get back to the camera. During this time, between sending the pulse and detecting the reflected pulse, the light does a round trip – it travels out and back again. The time the light takes to go one way is therefore half the measured interval. I'll call this time – half the time between sending and receiving the pulse – the transit time.

The speed of light is known, so the transit time can be used to calculate the distance between the camera and the object.

Specifically, the distance from the camera to the object is given by the transit time multiplied by the speed of light.

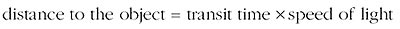
This can be written much more concisely using

• d for the distance to the object

• t for the transit time

• c for the speed of light.

Then I can write:

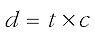
When writing equations like this, it is a convention that you can miss out the multiplication symbol. Any numbers or letters written next to each other are taken to be multiplied together, so we can write:

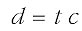
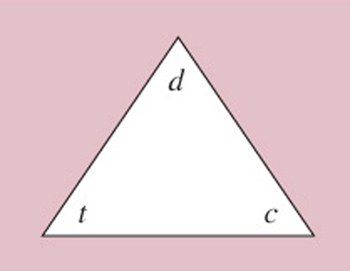
Equations relating three quantities in this particular way, where one (in this case d) is given by multiplying the other two (in this case t and c) together, are quite common, and you will be meeting other examples later in this course. For reasons which will become clearer later, it is useful to draw this type of equation in a 'formula triangle', as shown in Figure 8. The quantities that are multiplied together go in the bottom two corners (it doesn't matter which way around), and the thing they calculate goes in the top corner. I am not going to say anything more about the formula triangle for the moment, though it might be a bit mysterious, but it will become clearer later.

Figure 8 A formula triangle

I now want to put in a value for the speed of light, c, so that I will have a formula that allows me to calculate the distance d directly from the transit time t.

The speed of light in metres per second is 3×10⁸. That is to say, light travels 3×10⁸=300,000,000 metres every second. When I am doing calculations related to the focusing of the camera, however, I will find the times I am using will be much smaller than a second and the relevant distances will usually be of the order of a few metres – not three hundred million metres! What I am going to do, therefore, is express the speed of light in terms of how far it travels in one nanosecond (ns), which is one thousand-millionth of a second:

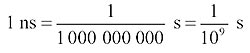
Activity 13

How far will light travel in one nanosecond?

Discussion

Light travels 300,000,000 metres in one second, so in one nanosecond it travels:

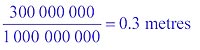
So I can express the speed of light as 0.3 m/ns (0.3 metres per nanosecond). But this means that when I write the equation, t represents a time in nanoseconds and d represents a distance in metres. It is important that all the units match. Using a value of c=0.3 m/ns and provided t and d are in nanoseconds and metres respectively, I get:

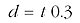
It doesn't matter which way round you write a multiplication (4×5 is the same as 5×4) and it is a convention always to put numbers before letters, so this would normally be written:

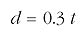
For example, if the transit time is 20 ns, the distance in metres is given by:

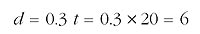
So the distance is 6 m.

Activity 14

If the transit time is 14 ns, how far away is the object?

Discussion

The distance in metres is given by:

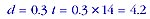
So the distance is 4.2 m.

Remember that the reason for discussing this calculation was to show that when using active focusing the camcorder can measure the distance to an object by transmitting and detecting an infrared pulse. Active autofocusing therefore involves another output from and input to the camcorder (sending and receiving the infrared pulse). We can show this by adding it to the high-level diagram of a camcorder that was shown in Figure 4, to get that shown in Figure 9.

Figure 9 Model of camcorder with active autofocusing

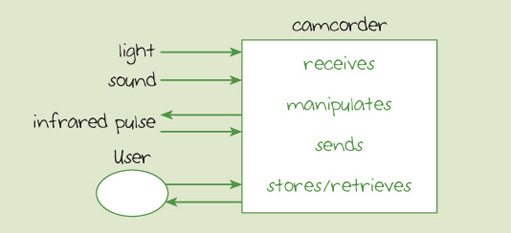
At a lower level of abstraction, the components of the active autofocusing are shown in Figure 10, together with other relevant components of the camcorder.

Figure 10 Active autofocusing

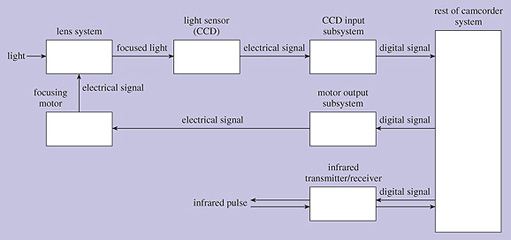
Figure 10 is similar to Figure 5, but I have removed the detail of the sound subsystem in order to concentrate on the light and focusing subsystems.