1.5 Plimpton 322
1.5.1 Uncertain origins
The tablet is called Plimpton 322, and is described by Neugebauer (The Exact Sciences in Antiquity (Dover, 1969) p. 40) as ‘one of the most remarkable documents of Old-Babylonian mathematics’. The name arises simply from the fact that the tablet has catalogue number 322 in the George A. Plimpton collection at Columbia University, New York. Plimpton bought it in about 1923 from a Mr Banks who lived in Florida; it is not certain where he obtained it, but it may have been dug up at Larsa in Mesopotamia. The left hand side of the original tablet appears to have been broken off, and traces of modern glue suggest that this has happened since its excavation. (All of this is a fairly typical example of the random, not to say slapdash, way in which things have emerged from under the sand into the eventual light of public knowledge.)

Look at the photograph and notice the main features of what remains: four columns of numbers, with words at the head of each column. Now look at the transcription (we have labelled the columns A, B, C for ease of reference), and see if any pattern is evident to you
| A | B | C | |
|---|---|---|---|
| [1;59,0,]15 | 1,59 | 2,49 | 1 |
| [1;56,56,]58,14,5O,6,15 | 56,7 | 3,12,1 | 2 |
| [1;55,7,]41,15,33,45 | 1,16,41 | 1,50,49 | |
| [1;]5[3,1]0,29,32,52,16 | 3,31,49 | 5.9,1 | 4 |
| [1;]48,54,1,40 | 1,5 | 1,37 | 5 |
| [1;]47,6,41,40 | 5,19 | 8,1 | 6 |
| [1 ;]43,11,56,28,26.4O | 38,11 | 59,1 | 7 |
| [1;]41,33,45,14,3,45 | 13,19 | 20,49 | 8 |
| [1;]38,33,36,36 | 9,1 | 12,49 | 9 |
| 1;35,10,2,28,27,24,26,40 | 1,22,41 | 2,16,1 | 10 |
| 1 ;33,45 | 45 | 1,15 | 11 |
| 1;29,21,54,2,15 | 27,59 | 48,49 | 12 |
| [1;]27,0,3,45 | 7,12,1 | 4,49 | 13 |
| 1;25,48,51,35,6,40 | 29,31 | 53,49 | 14 |
| [1;]23.13,46,40 | 56 | 53 | 15 |
At first sight, this is not very promising! Something seems to be being listed, as the lines are numbered (final column); and the numbers in column A do diminish fairly regularly, from just under 2, down to just over 1⅓. (But if you did manage to notice that it was partly the effect of the editorially informed semi-coIons, and Neugebauer's reconstructions in square brackets, of course.) Otherwise, the numbers look fairly random, and there is little to tell that this is not a Babylonian supermarket till receipt. (Until Neugebauer studied the tablet, it was, in fact, catalogued as a ‘commercial account’.) But Neugebauer discovered—presumably after a considerable amount of conjecture and refutation—that the numbers in each line can be related as:
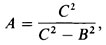
and this was the basis for his reconstruction of the illegible entries. Let us check this out on the simplest looking complete case, line 11.

So it is possible to find a relation, albeit a somewhat devious one, between the columns of the tablet. (In fact, for this to hold consistently throughout, the underlined numbers have to be considered as mistakes by the scribe, a point to which we shall return.) Before trying to decide what this is all about, let us investigate the numbers a little more. If we calculate C2−B2 for each entry, and then take its square root, something rather surprising emerges. Look at the next table, in which we have calculated the values (and the scribe's ‘errors’ have been corrected’). Ignore for the time being the final two columns which we have labeled p and q.
| B | C | p | q | ||
|---|---|---|---|---|---|
| (decimal) | (sexagesimal) | ||||
| 119 | 169 | 120 | 2,0 | 12 | 5 |
| 3367 | 4825 | 3456 | 57,36 | 64 | 27 |
| 4601 | 6649 | 4800 | 1,20,0 | 75 | 32 |
| 12709 | 18541 | 13500 | 3,45,0 | 125 | 54 |
| 65 | 97 | 72 | 1,12 | 9 | 4 |
| 319 | 481 | 360 | 6,0 | 20 | 9 |
| 2291 | 3541 | 2700 | 45,0 | 54 | 25 |
| 799 | 1249 | 960 | 16,0 | 32 | 15 |
| 481 | 769 | 600 | 10,0 | 25 | 12 |
| 4961 | 8161 | 6480 | 1,48,0 | 81 | 40 |
| 45 | 75 | 60 | 1,0 | ||
| 1679 | 2929 | 2400 | 40,0 | 48 | 25 |
| 161 | 289 | 240 | 4,0 | 15 | 8 |
| 1771 | 3229 | 2700 | 45,0 | 50 | 27 |
| 56 | 106 | 90 | 1,30 | 9 | 5 |
Notice that, compared wilh columns B and C, the values computed in D are remarkably simple looking numbers (this is particularly noticeable in their sexagesimal representation). You may indeed have recognised some as old friends, from the reciprocal table. In fact, all of them are regular numbers (whereas B and C are all, except for line 1L, non-regular), which explains why their squares could divide into C2 and yield an exact, finite sexagesimal expression.
