1.3.4 Vertically opposite angles
When two straight lines cross, they form four angles. In the diagram below, these angles are labelled α, β, θ and φ and referred to as alpha, beta, theta and phi. The angles opposite each other are equal. They are called vertically opposite angles. Here α and β are a pair of vertically opposite angles, as are θ and φ. Although such angles are called ‘vertically opposite’, they do not need to be vertically above and below each other!
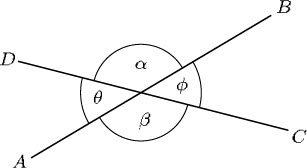
For two intersecting straight lines, vertically opposite angles are equal.
We can show that vertically opposite angles are equal as follows:
α and θ lie on a line.
So, α + θ = 180°
and α = 180° – θ
but β and θ also lie on a line.
So, β + θ = 180°
and β = 180° – θ.
Hence, α = β because they are both equal to 180° – θ.
