1.4.1 Corresponding angles
Look at the line l, which cuts two parallel lines m and n.
If you trace the lines at one of the intersections in the diagram below and place them over the lines at the other intersection, you will find that the two sets of lines coincide exactly. The four angles at each intersection also coincide exactly: thus α = a, β = b, γ = c and δ = d.
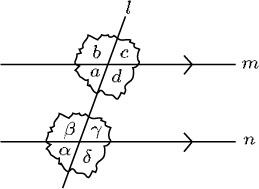
The pairs of angles that correspond to each other at such intersections are called corresponding angles.
In the diagram below, α and a are corresponding angles: they are equal because m and n are parallel.
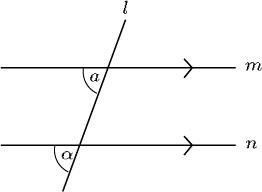
When a line intersects two parallel lines, corresponding angles are equal.
Example 5
This diagram represents the type of arrangement that occurs in a garden trellis or a wine rack (r and s are parallel lines, indicated by the single arrowheads; l and m are also parallel, indicated by the double arrowheads). Calculate the angles α and β.
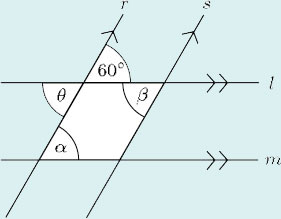
Answer
Line l is parallel to line m, therefore α and the angle 60° are corresponding angles. So α = 60°.
The angles 60° and θ are vertically opposite angles. So θ = 60°.
Line r is parallel to line s, therefore θ and β are corresponding angles. So β = 60°.
