1.4.2 Alternate angles
Other pairs of equal angles can be identified in Example 5. These pairs of angles occur in a Z-shape, as indicated by the solid line in the diagram below. Such angles are called alternate angles.
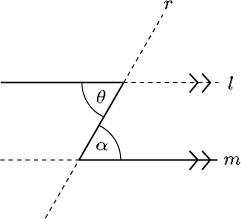
When a line intersects two parallel lines, alternate angles are equal.
To prove this result consider the diagram below:
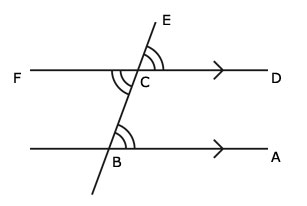
ABC = DCE (corresponding angles)
and DCE = FCB (vertically opposed angles)
So, ABC = FCB (both equal to DCE).
The other two angles are also equal and are also called alternate angles.
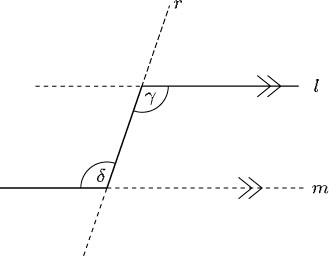
It is important to realise that you can find the sizes of unknown angles in many shapes by using a combination of the angle properties that have been outlined. To recap:
Vertically opposite angles are equal.
Angles at a point add up to 360°.
Angles on a straight line add up to 180°.
Corresponding angles on parallel lines are equal.
Alternate angles on parallel lines are equal.
Example 6
Find α and β in the following diagram.
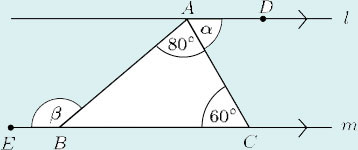
Answer
Line l is parallel to line m, therefore 
and 
are alternate angles. So
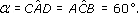
Similarly, 
and 
are alternate angles. But
and hence
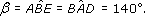
These properties of corresponding and alternate angles mean that the opposite angles in a parallelogram are also equal.