2.7 Rotational symmetry

There is another kind of symmetry which is often used in designs. It can be seen, for instance, in a car wheel trim.

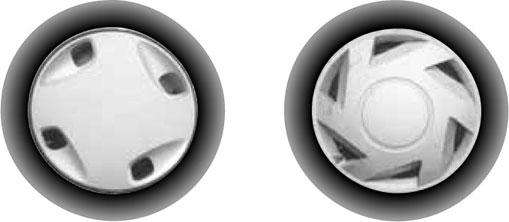
Look at the trim on the left. It does not have line symmetry but it has rotational symmetry. If the wheel is rotated through a quarter of a full turn, it will look exactly the same; likewise, if it is rotated through half a complete turn, or through three-quarters of a turn. There are four positions in which the wheel looks the same: hence the wheel is said to have rotational symmetry of order 4 or four-fold rotational symmetry.

The wheel trim on the right has rotational symmetry of order 6. In this case there are six positions in which the trim will look exactly the same. These occur when the wheel is rotated through one-sixth of a complete turn, two-sixths of a turn, and so on, to five-sixths of a turn and finally a complete turn (when, of course, the wheel is back in its original position).

The centre of the shape is the point about which the shape is rotated; it is called the centre of rotation.

A shape does not have to be round to have rotational symmetry. The following shapes have rotational symmetry of orders 3 and 4, respectively.

It is not difficult to create shapes with both line symmetry and rotational symmetry. The two designs below are examples.

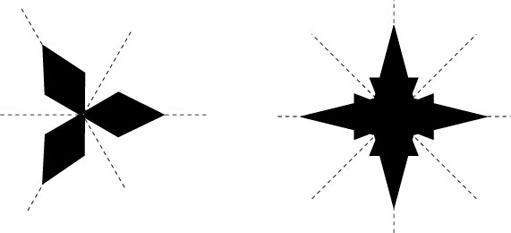
The design on the left has three lines of symmetry and rotational symmetry of order 3. The one on the right has four lines of symmetry and rotational symmetry of order 4.

A shape with no rotational symmetry, like the one below, is sometimes said to have ‘rotational symmetry of order 1’. This is because it will only fit on top of itself in one position – after a complete turn.