Try some yourself
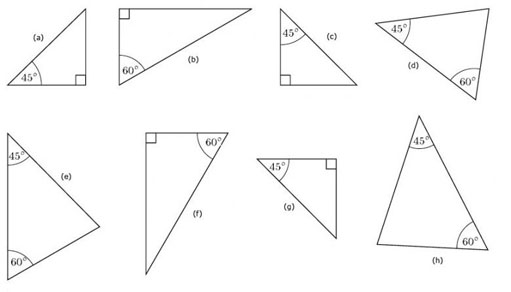
Question 1
Which of these triangles are similar?
Answer
Triangles a, c and g are similar since they have angles of 90°, 45° (and hence another angle of 45°).
Triangles b and f are similar since they have angles of 90°, 60° (and hence another angle of 30°).
Triangles d, e and h are similar since they have angles of 45° and 60° (and hence another angle of 75°).
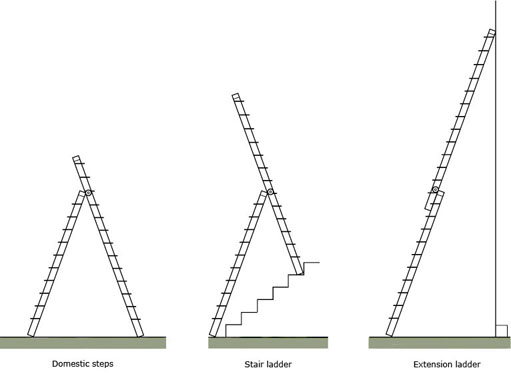
Question 2
An aluminium ladder can be used in three different ways:
The manufacturer says that in use, each segment of the ladder should make an angle of 20° with the vertical.
For each diagram, add construction lines and labels so as to identify two similar triangles. Are any of the similar triangles also congruent?
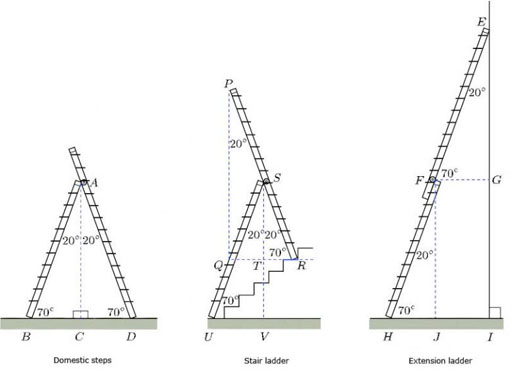
Answer
There are many alternative solutions.
Here are some similar triangles which are identified by using the labels given in the diagram above:
| domestic steps | ΔACD and ΔACB, |
| stair ladder | ΔSTR, ΔSTQ, ΔPQR, ΔSVU, |
| extension ladder | ΔFJH, ΔEIH, ΔEGF. |
Some congruent triangles are
| domestic steps | ΔACD and ΔACB, |
| stair ladder | ΔQST and ΔSTR. |
Question 3
This diagram shows the arrangement of the struts in a wall of a shed.
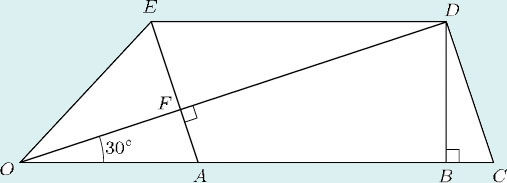
The lines OABC and DE are each horizontal. The struts EA and DC are parallel.
(a) Which of these are right angles?
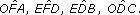
(b) Write down two angles that are equal to
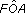
(c) Several of the triangles formed by the struts are similar (that is, they are the same shape). Write down all the triangles that are similar to ΔOAF.
Answer
3
(a) All four of the given angles are right angles.
(b)
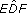(which is the same as 
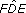) is equal to 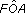. They are alternate angles.
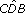(which is the same as 
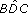) is equal to 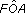. This is because ΔBCD and ΔOAF are similar: each has a right angle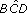, and 
and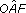 
are corresponding angles.(c) There are four triangles that are similar to ΔOAF: they are ΔOBD, ΔDEF, ΔOCD and ΔBCD.