3.2 Areas of circles
There are two very famous formulas for circles:
circumference of a circle = ![]() × diameter
× diameter
and
area of a circle = ![]() × radius2.
× radius2.
![]() is the Greek letter for ‘p’ and it has the name ‘pi’. Its value is approximately 3.14. Most calculators have a key for
is the Greek letter for ‘p’ and it has the name ‘pi’. Its value is approximately 3.14. Most calculators have a key for ![]() which you can use when carrying out calculations.
which you can use when carrying out calculations.
Try measuring the circumference and diameter of some circular objects such as tins, bottles or bowls. For each object, divide the circumference by the diameter. You should find that your answer is always just over 3. In fact the ratio is the constant ![]() . Therefore:
. Therefore:
Circumference of a circle = ![]() × diameter
× diameter
Since the diameter is twice the radius, this formula can be written as
circumference = ![]() × 2 × radius = 2
× 2 × radius = 2![]() × radius.
× radius.
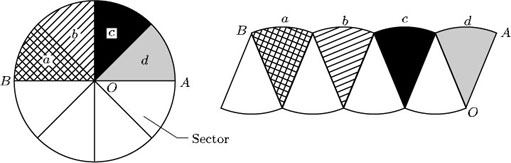
The formula for the area of a circle can be explained, as outlined below.
The circle here has been divided into equal ‘slices’ or sectors. The eight sectors can then be cut out and rearranged into the shape shown: this shape has the same area as the circle.
You can see that the total distance from A to B along the ‘bumps’ is the same as half the circumference of the circle, that is:
![]() × 2
× 2![]() × radius =
× radius = ![]() × radius. Also the length OA is the same as the radius of the circle.
× radius. Also the length OA is the same as the radius of the circle.
Imagine dividing the circle into more and more sectors and rearranging them as described above. For example, dividing the circle into 16 equal sectors gives the following shape, whose area is still the same as that of the circle.
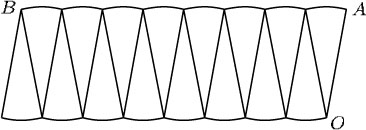
Again the total distance from A to B along the bumps is ![]() × radius, and the length of OA is the same as the radius.
× radius, and the length of OA is the same as the radius.
Notice how the rearranged shape is beginning to look more like a rectangle. The more sectors, the straighter AB will become and the more perpendicular OA will be. Eventually it will not be possible to distinguish the rearranged shape from a rectangle. The area of this rectangle will be the same as that of the circle, and its sides will have the lengths ![]() × radius (for AB) and radius (for OA). So the following formula can be deduced:
× radius (for AB) and radius (for OA). So the following formula can be deduced:
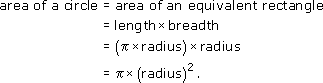
Area of a circle = ![]() × (radius)2
× (radius)2
Example 13
A circular flowerbed is situated in the centre of a traffic roundabout. The radius of the flowerbed is 10 m. Find its circumference and its area.
Answer
Circumference = 2![]() × radius = 2
× radius = 2![]() × 10 m = 20
× 10 m = 20![]() m ≈ 62.8 m
m ≈ 62.8 m
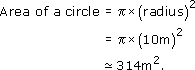
Example 14
A circular pond has a diameter of 7 m. A 1 m wide gravel path is to be laid around the pond. What is the area of the path?
Answer
The diagram shows the area of the path.
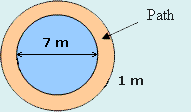
This area can be found by calculating the area of the path and pond together, and then subtracting the area of the pond.
So, Area of path = Area of path and pond – Area of pond.
The pond and the path form a circle of diameter 1m + 1m + 7m = 9m. A circle of diameter 9m has a radius of 4.5 m.
So, the area of the path and pond = ![]() × 4.52 m2.
× 4.52 m2.
The pond has diameter 7 m, so its radius is 7 m ÷ 2 = 3.5 m.
Hence, the area of the pond = ![]() × 3.52 m2.
× 3.52 m2.
So, the area of the path = ![]() × 4.52 m2 −
× 4.52 m2 − ![]() × 3.52 m2
× 3.52 m2
![]() 25 m2.
25 m2.