Try some yourself
Question 1
Find the volumes of these objects.
Answer
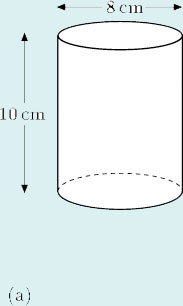
(a)
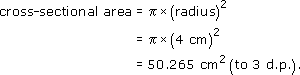
So
volume = 50.265 cm2 × 10 cm = 502.65 cm3.
Thus the volume is 503 cm3 (to the nearest cubic centimetre).
(If you used the approximate value of 3.14 for 
, you will have got a cross-sectional area of 50.24 cm2 and a volume of 502.4 cm3.)
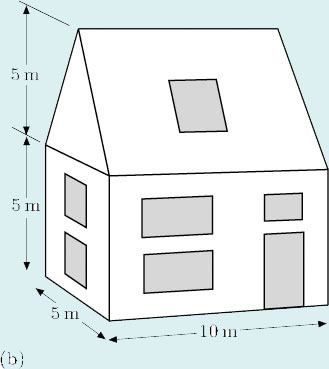
(b)
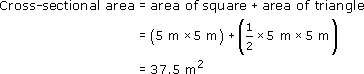
So
volume = 37.5 m2 × 10 m = 375 m3.
Question 2
Two car manufacturers both claim that their models have an engine capacity of 2 litres. The two models have four-cylinder, four-stroke engines.
The table below shows the details of the four cylinders.
| Car model | Cylinder diameter (bore)/mm | Cylinder height (stroke)/mm | Number of cylinders |
|---|---|---|---|
| A | 86 | 86 | 4 |
| B | 92 | 75 | 4 |
By working out the total volume of the four cylinders for each model in cm3, find out if the manufacturers’ claims are true.
(Hint: 1 litre = 1000 cm3.)
Answer
Car A has four cylinders, each with a radius of 4.3 cm and a height of 8.6 cm. The volume of one cylinder is calculated by using the formula
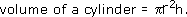
So, the four cylinders will have
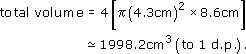
Car B has four cylinders, each with a radius of 4.6 cm and a height of 7.5 cm. From the same formula, the four cylinders will have
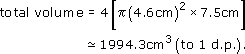
Therefore, both engines have a cubic capacity very close to 2000 cm3. They are both said to have two-litre engines. Hence the claims of both manufacturers are true.
Question 3
The guttering pictured here has a semicircular cross-section. Find the volume of water that the guttering will hold when full.
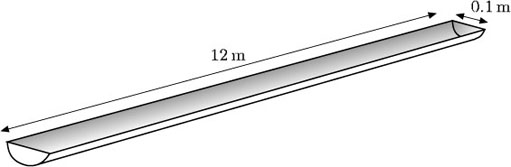
Answer
The cross-section of the guttering is a semicircle of radius 0.05 m. So
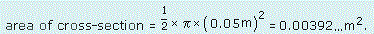
Then, since the length of the guttering is 12m,
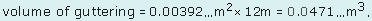
Therefore the guttering will hold about 0.047 m3 of water.