7.4 Spread
7.4.1 Range and inter-quartile range
So far in this section, you have seen that the mean, median and mode can all give a useful typical value of a set of data. However, there is further information that you can get from a set of data which can help to complete the picture.
Consider the following two sets of data.
Data set C: 113, 48, 26, 99, 64 The number of runs scored by a cricket batsman in a 5-week period.
Data set D: 72, 69, 74, 71, 70 A person's pulse first thing in the morning, measured over 5 days.
The mean for data set C is 70 and the mean for the data set D is 71.2.
Activity 18
What do you think is the most striking difference between these two sets of data?
Discussion
You might have said that the values in the first set are quite varied but the values in the second set are all very similar to one another. This is an important difference between the two sets of data.
It is useful to calculate the range of a set of values.
The smallest value in data set C is 26 and the largest is 113, so the range is
113 – 26 = 87.
The smallest value in data set D is 69 and the largest is 74, so the range is
74 – 69 = 5.
The range is easy to calculate and gives you a rough idea of how spread out the values in a set of data are. However, it does need to be treated with caution. The range depends on the two extreme values in a set of data and it is quite possible that one or both of them is untypical of the set.
Activity 19
Here are two sets of data. Which would you say was the more spread out?
Data set E: 1, 3, 4, 4, 7, 8, 10, 14, 15, 17, 17, 20
Data set F: 1, 8, 8, 8, 9, 9, 9, 10, 11, 11, 11, 20
Discussion
The range of both these sets of data is 20 − 1 = 19. However, data set E is more spread out than the data set F. Clearly, you need some way of spotting this, especially if you have a large number of values in your set of data.
In order to get a more accurate picture, you need to calculate a smaller range, nearer to the middle of the distribution, which avoids the extreme values.
The range to use is based on the quartiles of the distribution and is called the interquartile range. You already know how to find the median, which divides the set of values into two equal parts, so you now need to divide each of these two parts into two equal parts to get the quartiles. You might like to think of the quartiles dividing the range into quarters or four parts.
Consider data set E again:
1, 3, 4, 4, 7, 8, 10, 14, 15, 17, 17, 20
The median of this set of data is the mean of the two underlined numbers:
(8 + 10) ÷ 2 = 9
You now need to find the median of the first 6 values in the set; this value is (4 + 4) ÷ 2 = 4. The median of the second 6 values is (15 + 17) ÷ 2 = 16.
Thus, data set E can be divided into four parts by the three quartiles, Q1, Q2 and Q3with the second, Q2, having the same value as the median. The values used to calculate the quartiles are underlined.

Note that medians and quartiles may or may not be equal to one of the data values. You can now calculate the inter-quartile range, Q3 − Q1: 16 − 4 = 12. This gives a measure of the spread of the middle 50% of the data values.
Activity 20
Using data set F, calculate the quartiles and the inter-quartile range.
Data set F: 1, 8, 8, 8, 9, 9, 9, 10, 11, 11, 11, 20
Discussion
The median is (9 + 9) ÷ 2 = 9. The first quartile Q1 is (8 + 8) ÷ 2 = 8. The third quartile Q3 is (11 + 11) ÷ 2 = 11. The inter-quartile range forthis set of data is 11 – 8 = 3. Again, the values used to calculate the quartiles are underlined.
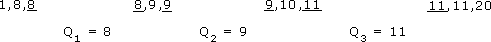
The inter-quartile range is Q3 − Q1: 11 − 8 = 3.
Although both sets of data have a range of 19, you now know that data set E has an inter-quartile range of 12 and data set F has an inter-quartile range of 3. Since half of the values lie within the inter-quartile range, a value of 12 suggests that the values of data set E might be quite spread out whereas a value of 3 suggests that while half the values of data set F are very close together, some values in this data set are not typical of all the data.
