1.4 Converting ratios from fractions to decimals
Although ratios are often given as fractions, they can also be expressed as decimals. You need to deal with a mixture of fractions and decimals, and to compare ratios given in either form, so you need to be able to convert between the two forms.
Example 4
The ratio of the circumference of a circle to its diameter is a constant denoted by 
(the Greek letter p) pronounced pi, it has been approximated by a number of different fractions. One such fraction is 
, another is 355/113. How do these compare with the decimal value from a calculator of 3.141592 654?
Answer
If you have a calculator handy then you could key in 22 ÷ 7 to convert to a decimal. However, if not, you might use long division or an informal method of division. Either way you should get 3.1428 …. So agrees to 3 significant figures.
You will probably find it easier to use a calculator for dividing 355 by 113. The result is 3.14159292, which agrees to 7 significant figures.
Sometimes you are given a ratio as a decimal, but might find it easier to use and/or remember as a fraction.
Example 5
Suppose you had been told that the ratio between a distance measured in miles and the same distance measured in kilometres is about 0.625. Convert this to a fraction.
Answer
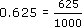
This fraction is an adequate answer, or you can divide top and bottom by common factors to reach a simpler equivalent fraction.
Divide top and bottom by 5 to get 
.
Divide top and bottom by 5 again to get 
.
Divide top and bottom by 5 again to get 
.
So the fraction is , which is the fraction used earlier.
An alternative method is do this in one line cancelling 