1 Squares, cubes and roots
1.1 Squares
In general, to square a number, multiply it by itself. This is denoted by writing a small ‘2’ to the top right of the number,
e.g. 4 squared, written 42, is 4 × 4 = 16.
Example 1
A gardener is planning to create a square patio using square concrete slabs. A row of 11 large slabs just fits across the width of the areas she wants to cover.
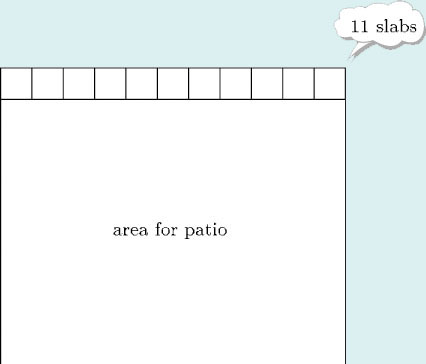
(a) How many rows of slabs will she use?
(b) How many slabs will she need altogether?
(c) The slabs are 0.75 m square. What area will the patio be?
Answer
(a) Since the patio is square and it is 11 slabs wide, it must be 11 slabs long too, so there are 11 rows of slabs.
(b) That means that altogether she will need 11 × 11, or 112 = 121 slabs.
(c) There are several ways of finding the area of the patio. One method is to say that each slab is 0.75 m by 0.75 m, which is an area of 0.752 square metres. So the patio is 112 × 0.752 square metres. Using a calculator gives 68.0625 square metres. An alternative method is to say that each side of the patio is 11 × 0.75 m. so the area of the patio is (11 × 0.75)2 square metres. Using a calculator again gives 68.0625 square metres. (Notice (11 × 0.75)2 = 112 × 0.752.)
So the patio will be just over 68 square metres.
Example 2
In an art course the teacher plans to asks each of the pupils to draw a sketch of every child in the class, including a self-portrait, on separate sheets of paper. There are 26 children in the class. Find an upper estimate for the number of sheets of drawing paper he should supply for the whole class. Find a lower estimate. Use your calculator to find the exact number of sheets of paper.
Answer
Each of the 26 children will need 26 pieces of paper, so altogether 26 × 26, i.e. 262 sheets of paper are required.
Upper estimate: If there were 30 pupils in the class he would need 30 × 30 = 900 sheets of paper.
Lower estimate: If there were only 20 pupils the teacher would need 202 = 400 sheets of paper.
So he will need something in between 400 and 900.
On the calculator, 262 = 676.
This is in reasonable agreement with the rough check, so 676 sheets of paper are required. (He would probably take 700 to have spares.)
