2.6 Negative powers

Now look at what happens when the power is negative. What does 10⁻³ mean? What is the result of the following calculation?

100 ÷ 100 000

What you are actually being asked to find is:

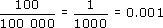
But look at the calculation again. Using the rule for the division of powers of numbers gives:

10² ÷ 10⁵ = 10²⁻⁵ = 10⁻³

So 10⁻³ = 0.001. But you can also write this result as:

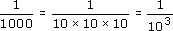
This means that 10⁻³ can be thought of as 1 divided by 10³.

This result is true for all negative powers, not just powers of ten. For example:

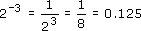
One over any number is called the reciprocal of the number.

For example, the reciprocal of 10 is = 10⁻¹ and the reciprocal of 100 is = = 10⁻²

So 10⁻⁵ = = 0.00001.

Example 8

The decimal place value table columns are headed tenths, hundredths, thousandths etc. Write these as powers of ten.

Answer

  a tenth = =10⁻¹

  a hundredth = = 10⁻²

  a thousandth = = 10⁻³

So the headings of the place value table are all powers of ten. To the left of the units they are positive powers, the units column is 10⁰, and to the right the column headings are negative powers of ten.

Notice that

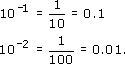
The negative power indicates the position of the decimal point — how many times it has moved to the left from 10⁰ = 1.

10⁻¹ = 0.1 (move one to the left); 10⁻² = 0.01 (move 2 to the left) etc.