2.6.1 Try some yourself
Activity 28
Find each of the following by hand, giving your answers both as a power of ten and as a decimal number. You will use these answers as a check on your calculator work in the next question.
(a) 10−2
(b) 102 × 103
(c) 107 ÷ 104
(d) 104 ÷ 107
(e) 2−2
Answer
(a) 10−2 = 0.01
(b) 102 × 103 = 102 + 3 = 105 = 100 000
(c) 107 ÷ 104 = 107 − 4 = 103 = 1000
(d) 104 ÷ 107 = 104 − 7 = 10–3 =
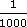= 0.001(e) 2−2 =
= 
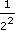(=0.25)
Activity 29
Evaluate the following, using your calculator and your answers from Question 1 as estimates.
(a) 10.3−2 (to four significant figures)
(b) 10.12 × 10.113 (to four significant figures)
(c) 10.1127 ÷ 10.214 (to one decimal place)
(d) 10.124 ÷ 10.3517 (to three significant figures)
(e) 2.2−2
Answer
Using Question 1 as a rough check, the calculator gives:
(a) 10.3−2 = 0.009 426 (to 4 s.f.)
(b) 10.12 × 10.113 = 105 400 (to 4 s.f.)
(c) 10.1127 ÷ 10.214 = 994.8 (to 1 d.p.)
(d) 10.124 ÷ 10.3517 = 0.000824 (to 3 s.f.)
(e) 2.2−2
0.2066
It is a good idea to get in the habit of estimating your answers, even if not specifically asked to do so.
Activity 30
Find each of the following by hand.
(a) 10240
(b) 10241
(c) 5−1
(d) 10−4
Answer
(a) 10240 = 1
(b) 10241 = 1024
(c)
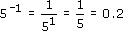
(d)
Activity 31
How many zeros are there after the decimal point in the number 10−6? How many zeros are there after the decimal point for any given negative power of 10?
Answer
10−6 = 0.000 001; there are five zeros after the decimal point. For any given negative power of 10, say 10−(NUMBER) there is one fewer zero than NUMBER. This works for 10−1, too, since 10−1 = 0.1, which has no zeros after the decimal point, i.e. one fewer than 1.
Activity 32
Try to answer the following questions
(a) Explain why a negative power of a number is one divided by the corresponding positive power of that number. (Hint: remember that a number to the power zero is 1.)
(b) Use the power button on your calculator to find the following.
(i)
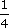
(ii)
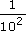
Answer
(a) Take an example, which makes the explanation easier than describing it in the abstract. Consider 10−6. Now −6 is just the same as 0 − 6, so 10−6 = 100−6. Using the rule for dividing powers, 100−6 = 100 ÷ 106. But 100 = 1. So 10−6 = 1 ÷ 106. This argument would apply equally well to any number, since any number to the power 0 is 1. (Alternatively you may have started from the other end, for example, by showing that
= 
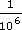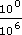= 100−6 = 10−6.)(b)
