5.2 Doing and undoing

Now try the following.

Think of a number. Add 4. If my answer is 11, can you work out what number I was thinking of?

You might have said ‘What number do I have to add on to 4 to get 11?’ or perhaps ‘If I take away 4 from 11 what number do I get?’ In both cases you should have arrived at the answer 7.

In the second method ‘subtracting 4’ undoes the ‘adding 4’ in the original instructions.

This process can be illustrated by a ‘doing–undoing diagram’.

Figure 16

In the doing part of the diagram, start with the number and write down the operations applied in turn until you get the answer. Here there is just one operation ‘add 4’.

Figure 17

For the undoing part of the diagram, start on the right with the answer, in this case 11. Then work back towards the left, undoing each operation in turn until you find the starting number. In this case, ‘subtract 4’ undoes ‘add 4’ and 11 minus 4 = 7. So, the number first thought of was 7. Notice how the arrows indicate the direction to read the diagram.

The next activity gives you some practice with doing and undoing. You will find these techniques helpful for rearranging formulas. Part (d) involves two stages.

Activity 16: Doing and undoing

Try to work out what number I was thinking of in the following problems.

You may find it helpful to use some doing–undoing diagrams.

• a.Think of a number, subtract 3 and the answer is 2.

• b.Think of a number, multiply by 5 and the answer is 35.

• c.Think of a positive number, square it and the answer is 81.

• d.Think of a number, add 4, double it and the answer is 14.

Discussion

(a)

Figure 18

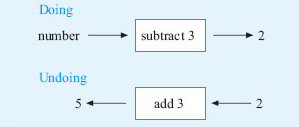
So the number I thought of was 5.

Remember you can check your answer by using it in the trick: 5 − 3 = 2.

(b)

Figure 19

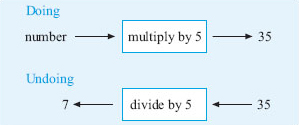
So the number I thought of was 7. (Check: 7 × 5 = 35. )

(c)

Figure 20

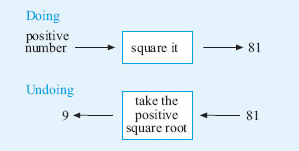
So the number I thought of was 9. (Check: 9² = 81. )

(d)

Figure 21

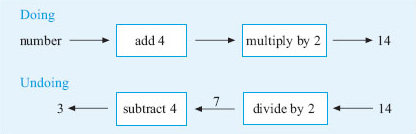
So, working from the right, 14 ÷ 2 = 7 and 7 − 4 = 3.

If you like, you can write the output from each box on the arrow as shown above.

Hence, the number I thought of was 3. (Check: 3 + 4 = 7; 7 × 2 = 14. )

When you have to deal with more than one operation, just take each step in turn. Write down the doing diagram and draw the undoing one underneath, working backwards to undo each operation.

To summarise, the following operations undo each other:

• addition and subtraction

• multiplication and division

• squaring and taking the positive square root.

Activity 17: A multi-step problem

Think of a number. Add 5. Multiply by 3. Subtract 4.

If the answer is 17, can you work out what number I was thinking of?

Here there are several steps, so to find the number it will be necessary to undo each of these steps in turn, starting with the last step. Draw the doing diagram and then the undoing one beneath it.

Discussion

The diagram below shows the steps taken in this case and then how to undo each one.

Figure 22

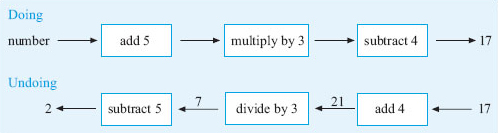
So if the answer is 17, undoing the steps by working from right to left gives:

add 4:	17 + 4 = 21
divide by 3:	21 ÷ 3 = 7
subtract 5:	7 − 5 = 2

So the number I thought of was 2. (Check: 2 + 5 = 7; 7 × 3 = 21; 21 − 4 = 17. )

The same sort of technique can be used to change formulas around. For example, earlier in the course, you found a formula to convert pounds into euros:

  number of euros = number of pounds × 1.48.

However, what if you wished to convert euros into pounds, say while you were shopping on holiday?

Then you would need a formula for the number of pounds based on the number of euros. We can tackle this by drawing the ‘doing and undoing’ diagrams for this situation:

Figure 23

So, starting at the right of the undoing diagram, the formula for converting euros into pounds is:

  number of pounds = number of euros ÷ 1.48.

Activity 18: Miles and kilometers

To change kilometres into miles, you used the formula:

  distance in miles = distance in kilometres × 0.6214.

Starting with ‘distance in kilometres’, draw a doing diagram to get the distance in miles. Draw the undoing diagram and hence write down the formula for changing miles into kilometres.

Your formula should start ‘distance in kilometres =’.

Discussion

The doing and undoing diagrams are shown below.

Figure 24

So the formula for converting miles into kilometres is

  distance in kilometres = distance in miles ÷ 0.6214.

Activity 19: How many minutes for chatting?

Recall the formula for the monthly cost in £ of a mobile phone that we used earlier:

  monthly cost in £ = 15 + (total number of minutes − 30) × 0.1.

The owner wishes to stick to a monthly budget of £25. Starting with the ‘total number of minutes’, draw a doing diagram to show the operations to find the ‘monthly cost’. Put the monthly cost equal to £25 and then draw an undoing diagram to work out how many minutes of phone calls can be made if the monthly cost is £25.

Discussion

Here is the doing diagram.

Figure 25

Undoing each step in turn gives the following undoing diagram.

Figure 26

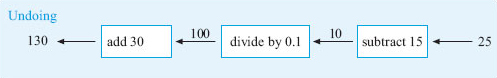
So applying these operations in turn:

subtract 15 gives 25 − 15 = 10,

divide by 0.1 gives 10 ÷ 0.1 = 100,

add 30 gives 100 + 30 = 130.

Hence, 130 minutes can be used for a monthly budget of £25.

With practice, this process of using a doing–undoing diagram does become second nature. In some cases, it can be useful if you need a formula in a different form. However, for complicated formulas, a different approach (which you will meet if you continue your mathematical studies) is often used.