6 Proportion
6.1 Direct proportion
The first type of proportion relationship is known as direct proportion. Two quantities are said to be directly proportional to each other if when one doubles, triples, quadruples, the other also doubles, triples, quadruples. For example, if you buy three times as many items as usual, you would expect to have to pay three times as much money (unless there was some special offer available), because the price is directly proportional to the number of items bought.
Activity 20: Directly proportional relationships
Which of the following quantities are in direct proportion?
-
(a) The number of kilometres and the equivalent number of miles in Activity 18.
-
(b) The number of euros that are exchanged for pounds in Activity 3.
-
(c) The monthly cost of a mobile phone and the minutes used for talking in Activities 6 and 7.
Discussion
Parts (a) and (b) are both examples of direct proportion. If you multiply the number of kilometres by any factor, the number of miles will also change by this factor. For example, if you double the number of kilometres, the number of equivalent miles will also double, and similarly for exchanging currency. If you triple the number of pounds you exchange, you would expect to get three times as many euros. However part (c) is not a directly proportional relationship. If you use 30 minutes, the charge is £15. But if you double the time used to 60 minutes, the charge is £18, and the price has not doubled.
You can tackle problems involving direct proportion in many different ways – using a formula is not always the easiest way, as the following example shows.
Suppose that in a tea club at work, a group of people share a carton of milk each day, but provide their own tea. The carton contains enough milk for 12 cups of tea. If the carton costs 36p, how much should someone who has four cups of tea with milk pay?
This person had ![]() of the milk, so should pay
of the milk, so should pay ![]() of the cost of the milk which is 12p.
of the cost of the milk which is 12p.
Alternatively, you can work out the cost of milk for one cup of tea as a first step.
Since there is enough milk for 12 cups, one cup will cost 36p ÷ 12 = 3p.
So four cups will cost 4 × 3p or 12p.
Note how the problem has been simplified by considering just one cup of tea first!
Activity 21: The more the merrier
A recipe for a vegetable curry for four people requires 300 g of rice. By first working out how much rice one person requires, calculate how much rice would be needed for nine people.
Discussion
Work out the amount of rice for one person: 300 g ÷ 4 = 75 g.
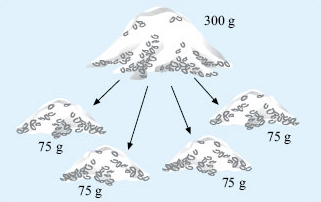
So nine people will need 9 × 75 g = 675 g.
(You can work this out in other ways too!)
Activity 22: How much medicine?
A patient needs to have 600 mg of a drug each day, given in three doses. Each tablet contains 100 mg of the drug. How many tablets are needed for each dose?
Discussion
One tablet contains 100 mg of the drug.
So six tablets will contain 600 mg of the drug. The patient will need to take six tablets spread over three doses.
So the number of tablets in each dose will be 6 ÷ 3 = 2.

You can also use a formula here:

Use the formula to see if you get the same answer.
Remember to check that your answer seems reasonable!
