6.2 Inverse proportion

The second type of proportional relationship is known as inverse proportion.

Suppose you have decided to hire a taxi to take a group of colleagues from work to the railway station. If the taxi firm charges a set fee for the journey, then the more people who go in the taxi, the less each person has to pay: if two people go, each pays half the cost; if three people go, each pays a third of the cost and if four people go, each person pays a quarter of the cost. This is an example of inverse proportion. As one quantity (the number of people) doubles or triples, the other quantity (the cost) halves or is reduced to a third of the original value. In other words if you multiply one quantity by a factor, the other quantity is divided by that factor.

The cost per person can be calculated directly or by using the formula:

  cost per person in £ = taxi fare in £ ÷ number of people.

For example, if the fare is £7.80 and four people go in the taxi, each person will have to pay £7.80 ÷ 4 = £1.95.

Two quantities are said to be inversely proportional if their product is a constant. For example, suppose you go on a journey of 30 km and it takes you an hour to get there. Your average speed for the journey is 30 km per hour. Now if you doubled your speed to 60 km per hour, it would take you half as long (that is, half an hour) to get there; if you halved your speed, it would take twice as long and so on. In each case, the following relationship holds:

(speed in km per hour) × (time for journey in hours) = (distance travelled in km).

This shows that for a given distance speed and time are inversely proportional to each other.

This formula can also be written as:

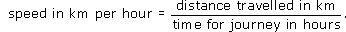
Activity 23: How fast?

For the journey of 30 km above, what is the average speed if the journey took 1 hours?

Discussion

Substituting the distance as 30 and the time as the decimal 1.5 in the formula above gives:

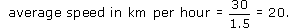
So the average speed is 20 km per hour.