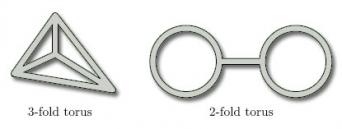
2.2.2 Hollow tubing surfaces

In their doughnut-shaped representation, toruses can be thought of as being hollow tubes. Many other surfaces in space can also be drawn as if they were made of hollow tubing. Figure 15 shows two such examples.

Figure 15

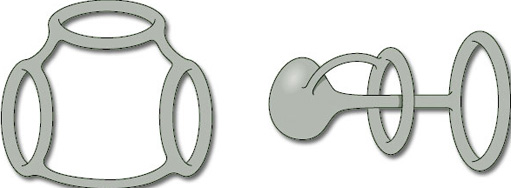
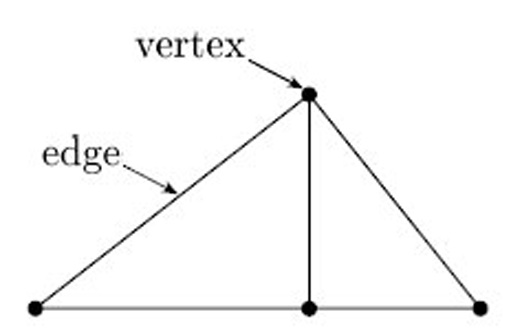
There is an easy way of constructing hollow tubing surfaces. Start with a finite set of points in three-dimensional space, called vertices, and connect them together by a finite set of lines, called edges, that meet only at the vertices, as shown in Figure 16: such a configuration is called a connected graph. We then obtain a surface by ‘thickening each edge’ of the connected graph into a hollow tube, as illustrated in Figure 17: the resulting surface, called a thickened graph, can be thought of as a hollow tube wrapping the original connected graph.

Figure 16 Connected graph with 4 vertices and 5 edges

Maximise

Figure 17

Problem 5

For each of the connected graphs in Figure 18, draw the associated thickened graph.

Figure 18

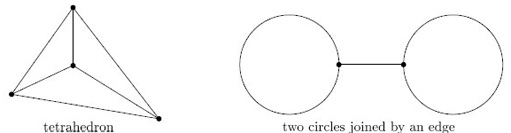
Answer