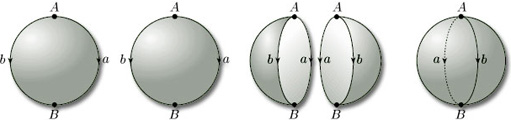
2.3.8 Sphere

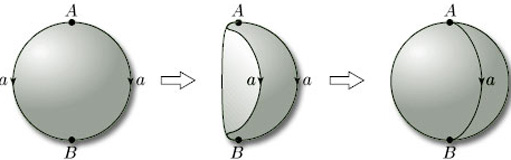
Surfaces can be constructed in a similar way from plane figures other than polygons. For example, starting with a disc, we can fold the left-hand half over onto the right-hand half, and identify the edges labelled a, as shown in Figure 36; this is rather like zipping up a purse, or ‘crimping’ a Cornish pastie. We can then stretch and inflate the object so obtained until we obtain a sphere.

Figure 36 Making a sphere from a disc

We can even start with more than one plane figure. For example, a sphere can be formed from two discs by identifying edges as shown in Figure 37 and then inflating.

Maximise

Figure 37 Making a sphere from two discs

Problem 9

Which surfaces are obtained by identifying edges (in the given directions) in each of the triangles in Figure 38?

Figure 38

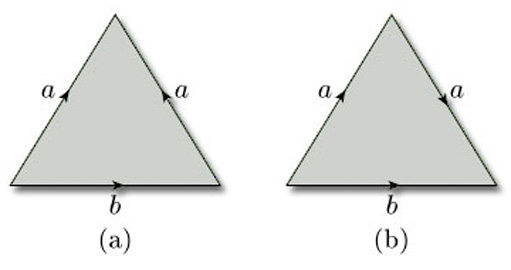
Hint: In (b), you might consider cutting the triangle before identifying the edges, and then repairing the cut.

Answer

(a) Identifying the edges we obtain a cone which can then be flattened out. The result is a disc.

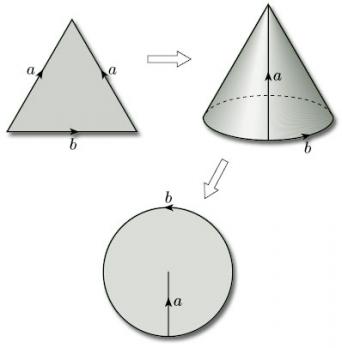
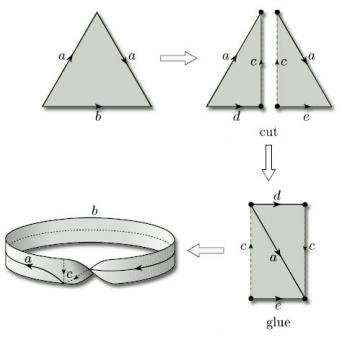
(b) The three vertices of the triangle are all identified to a single point which lies on the boundary of the resulting surface; the two edges that are identified become a single closed curve through this point. The result is a Möbius band. One way of seeing this is to bisect the triangle, glue the two parts together by identifying the edges labelled a, to create a rectangle, then repair the bisection (which needs a twist).

Throughout this section, our emphasis has been on describing the edge identifications geometrically. A more rigorous treatment, involving the so-called ‘identification topology’, is given in Section 5.