2.5 Defining surfaces
In Section 2.1 we gave a provisional definition of a surface. The aim of this section is to formalise that definition. To do that, we need to specify three further requirements of a candidate topological space, beyond those given in the provisional definition.
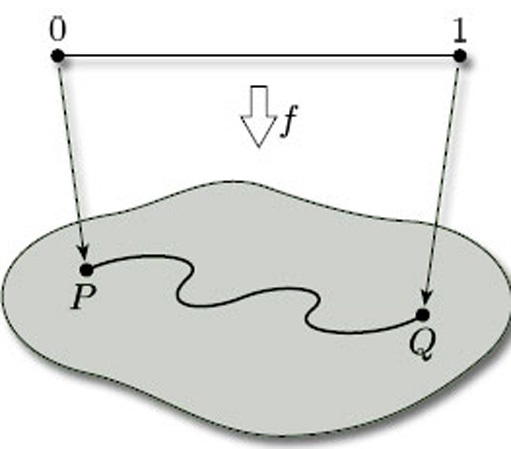
The first requirement is that the surface should be in ‘just one piece’. We can ensure this by requiring the surface to be path-connected: this means that any two points P and Q on the surface can be joined by a curve that lies entirely in the surface. In mathematical terms, this means that there is a continuous map f from the interval [0, 1] to the surface, such that f(0) = P and f(1) = Q (see Figure 45).
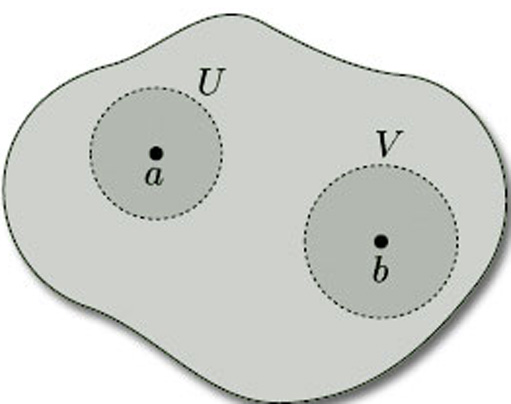
The second requirement is a technical one that is needed to eliminate certain awkward cases. We require a surface to be a Hausdorff space: this means that, given any pair of distinct points a and b in it, there are disjoint open sets U and V, one containing a and the other containing b, as shown in Figure 46. (We can think of the points a and b as being separated, or ‘housed orff’, from each other by open sets!) Hausdorff spaces are named after their originator Felix Hausdorff (1868–1942).
Not all topological spaces are Hausdorff: for example, the topological space consisting of the set X = {a, b} with the indiscrete topology is not Hausdorff, since the only non-empty open set is X itself, which does not separate a from b. However, 
3 with the Euclidean topology is Hausdorff, as is any subset of it with the induced topology: so surfaces in space are Hausdorff. Thus, for a topological space to be a surface in space, it must be Hausdorff.
Being path-connected and being Hausdorff are both topological invariants: thus, if two topological spaces are homeomorphic and one of them is path-connected, then so is the other; and, if one of them is Hausdorff, then so is the other.
Our final requirement for a surface is that it be compact. Such surfaces can be defined in a number of ways. For our purposes in this course, we shall think of compact surfaces as follows:
Definition
A compact surface is a surface that can be obtained from a polygon (or a finite number of polygons) by identifying edges.
For example, the surfaces we constructed in Section 2.3 – cylinder, Möbius band, torus, Klein bottle, projective plane, torus with 1 hole, 2-fold torus and sphere – are all compact surfaces. Examples of surfaces that are not compact are a cylinder without its bounding circles and the entire plane. Compactness is also a topological invariant, so any topological space that is homeomorphic to a compact surface is also a compact surface.
The importance of compact surfaces is that they are precisely the surfaces that we can classify by means of the Classification Theorem, which we state in Section 4. This is because they are the surfaces for which we can guarantee that the numbers used to classify surfaces are finite. For other types of surface, it can be very difficult to decide when two surfaces are homeomorphic.
Including the three new requirements that a surface be path-connected, Hausdorff and compact, we are able to turn our provisional definition of a surface into a formal definition.
Definition
A surface is a compact path-connected Hausdorff topological space (X,T) with the property that, given any point x 
X, there is an open set U containing x such that U is homeomorphic either to an open disc in 2 with the Euclidean topology or to an open half-disc in the upper half-plane with the subspace topology inherited from the Euclidean topology on 2.
A surface in space is a surface (X, TX) where X is a subset of 3 and TX is the subspace topology on X inherited from the Euclidean topology T on 3.