3.2 Orientability

The idea of orientability is another fundamental concept that we need for the study of surfaces. To illustrate the underlying idea, we consider two familiar surfaces – a cylinder and a Möbius band.

We can distinguish between a cylinder and a Möbius band by noticing that every cylinder has an ‘inside’ and an ‘outside’, as shown in Figure 53, and we can paint one red and the other blue. But if we try to paint a Möbius band in two colours, we fail – it has just one ‘side’. Equivalently, an ant crawling on a Möbius band can visit all points of the surface without crossing the boundary edge, whereas an ant on a cylinder can visit only the inside or the outside without crossing the boundary edges.

Figure 53

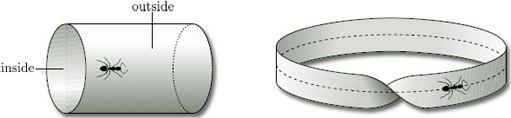
Two-sided surfaces in space, such as a cylinder, are examples of orientable surfaces, whereas one-sided surfaces in space, such as a Möbius band, are examples of non-orientable surfaces.

An orientable surface is one where consistent ‘orientation’ can be assigned over the entire surface; a non-orientable surface is one where this cannot be done.

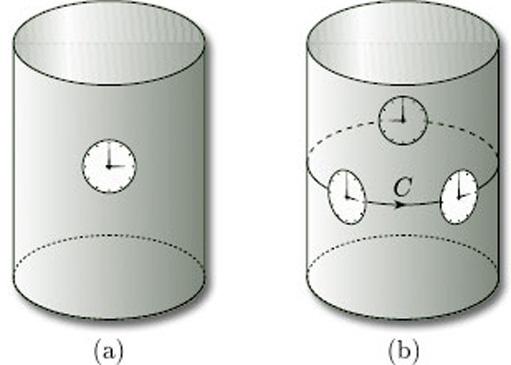
To see what we mean by this, let us take a cylinder and place on its surface a clock face whose minute hand is fixed at 12 and whose hour hand is fixed at 3, as shown in Figure 54(a): notice that the hour hand is found by going through /2 radians clockwise from the minute hand.

If we now slide the clock face along any closed curve on the surface, keeping the hour hand pointing along the curve, then the hour hand is always /2 radians clockwise from the minute hand: for example, if the hour hand moves along the curve C shown in Figure 54(b), then the clock face continues to show 3 o'clock. This means that we can consistently define ‘clockwise’ at any point of the surface: the hour hand is always /2 radians clockwise from the minute hand.

Figure 54

A similar situation occurs if we slide a clock face along any closed curve C on the surface of a sphere or a torus, as shown in Figure 55: in each case the hour hand is always /2 radians clockwise from the minute hand, and so we can again define ‘clockwise’ consistently.

Figure 55

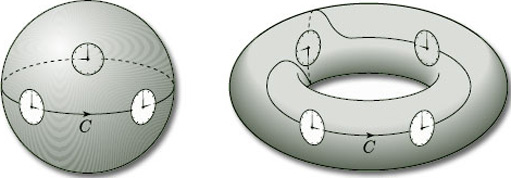
Orientable surfaces are surfaces for which we can define ‘clockwise’ consistently: thus, the cylinder, sphere and torus are orientable surfaces. In fact, any two-sided surface in space is orientable: thus the disc, cylinder, sphere and n-fold torus, all with or without holes, are orientable surfaces.

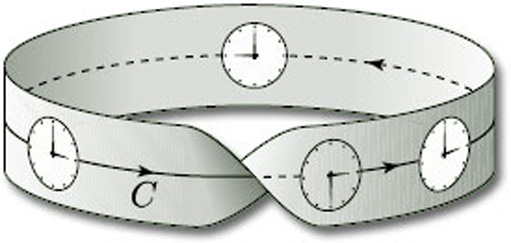
Let us now consider a clock face on a Möbius band, and let us slide it around the central curve C, as shown in Figure 56. Starting from any point on the curve, the twist in the surface causes the clock face to be upside-down when it first returns to that point: the hour hand still points to 3, but the minute hand now points downwards. Thus, the hour hand is no longer /2 radians clockwise from the minute hand. This means that we cannot consistently define ‘clockwise’ at every point of a Möbius band. Thus, the Möbius band is a non-orientable surface. In fact, any one-sided surface in space is non-orientable.

Figure 56

As we shall soon see, the Klein bottle and projective plane are also non-orientable.

Just as we use the boundary number β to distinguish between surfaces without boundary (β = 0) and surfaces with boundary (β > 0), so we introduce a number that distinguishes between orientable and non-orientable surfaces. This is another of the three characteristic numbers we use to classify compact surfaces.

For example, ω = 0 for the disc, cylinder, sphere and n-fold torus, all with or without holes, and ω = 1 for the Möbius band.

As you might expect, we have the following result, which tells us that the orientability number is a topological invariant.

One way of determining the orientability number of a given surface is to ascertain whether the surface contains a Möbius band.