3.2.1 Remarks
-
By ‘contains’, we mean that we can find part of the surface that is homeomorphic to a Möbius band. The edge of the Möbius band does not need to correspond to an edge at the surface, so that a surface without boundary can be non-orientable (as we shall shortly see).
-
When seeking Möbius bands in a surface, it can be helpful to look at all possible closed curves on the surface and thicken these into bands.
-
Remember, from Section 3.1, that all bands with an odd number of half-twists (in the same direction) are homeomorphic to Möbius bands.
Worked problem 2
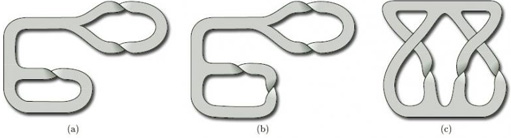
Determine whether each of the paper surfaces in Figure 57 is orientable.

Solution
(a) The top and middle of this surface have two half-twists each. These can be cut and glued back together to give the surface in Figure 58.

This surface is a disc with 2 holes, which is orientable (ω = 0).
(b) This surface contains several Möbius bands, two of which correspond to the closed curves shown in Figure 59.
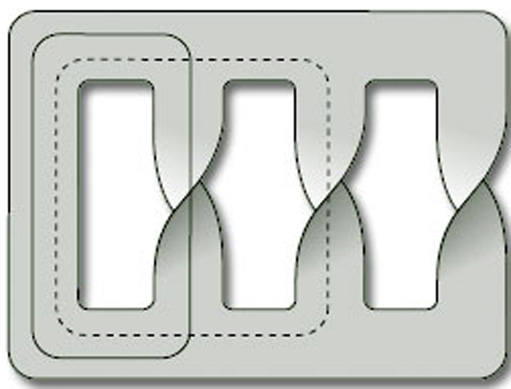
The surface is therefore non-orientable (ω = 1).
Problem 14
Answer
(a) This surface contains a Möbius band, indicated by the closed curve, so is non-orientable (ω = 1).

(b) This surface contains no Möbius bands, so is orientable (ω = 0).
(c) This surface contains several Möbius bands, one of which is indicated by the closed curve, so is non-orientable (ω = 1).

Theorem 4 can be applied to all types of surface, not just paper surfaces. It can even be applied to representations of surfaces as polygons with edge identifications, as we shall see in Section 3.3, where we show that the projective plane and the Klein bottle are non-orientable.