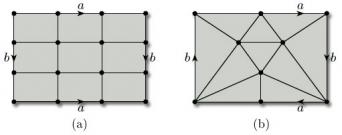
4 The Euler characteristic

4.1 Nets on surfaces

In Section 4 we introduce the third of the numbers we associate with a surface – the Euler characteristic. This is used in the Classification Theorem, which we state at the end of the section. To define the Euler characteristic, we need the idea of a subdivision of a surface, which we introduce by first considering the informal idea of a net on a surface.

To define the Euler characteristic, we need the idea of covering a surface with a net of polygons. To explain what we mean let us look at some examples.

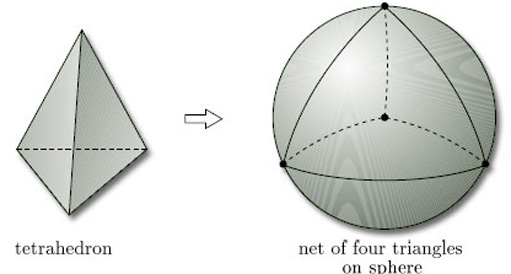
We start with a sphere and draw triangles upon it. One way to do this is to start with a tetrahedron, which (when considered as a polyhedral surface) is homeomorphic to the sphere. If we now ‘inflate’ the tetrahedron to obtain a sphere, the four triangular faces of the tetrahedron create a net of four triangles on the sphere, as Figure 71 illustrates. Here the word ‘triangle’ means any three-sided region drawn on a surface. They usually have curved sides and are not flat.

Figure 71

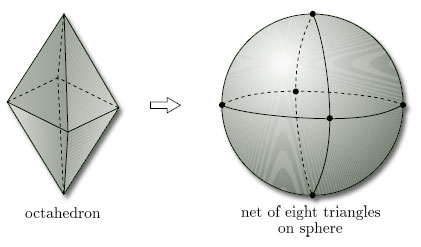
We can similarly inflate an octahedron, as shown in Figure 72.

Figure 72

We can also draw nets of triangles on other surfaces, such as the torus, for which it is convenient to show the net on the representation of the torus as a rectangle with edge identifications, as in Figure 73.

Figure 73

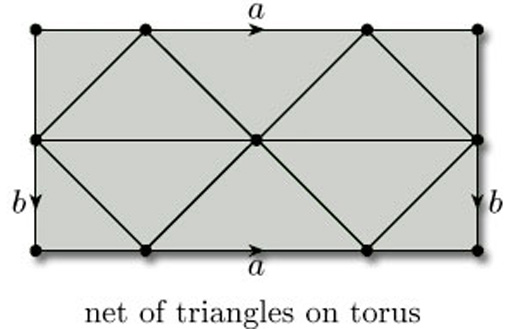
Remember that here the edge identifications a and b apply to the whole of the horizontal and vertical edges of the rectangle. For the sake of clarity, we assume that all parts of the edges of the defining polygon correspond to edges of the net.

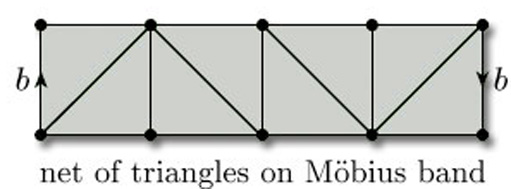
When we draw triangles on a surface with boundary, unless stated otherwise, we require that the boundary is decomposed into edges that are edges of the triangles. For example, Figure 74 shows a net of triangles on a Möbius band, again shown as a rectangle with edge identifications.

Figure 74

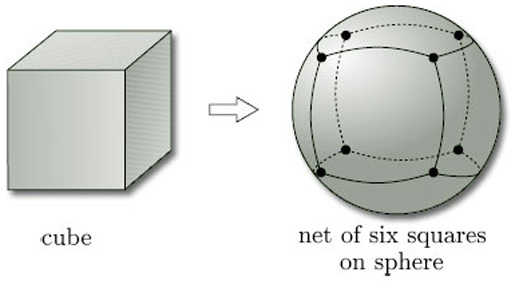
We need not restrict our attention to triangles: we can use polygons with any number of sides. For example, a cube can be inflated to give us a net of squares on a sphere, as Figure 75 shows.

Figure 75

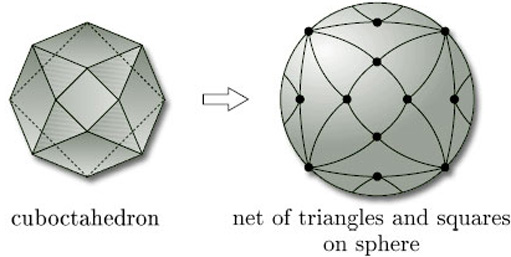
We can also use different types of polygon on the same surface. Figure 76 shows a net of triangles and quadrilaterals on a sphere, obtained by inflating a polyhedron called the cuboctahedron.

Figure 76

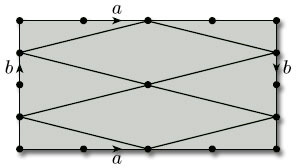
The surfaces we are considering include both surfaces in space and surfaces that cannot be represented in ³, such as the Klein bottle and the projective plane. For example, Figure 77 shows a net of quadrilaterals on a Klein bottle, shown as a rectangle with edge identifications. Note that the faces that look like triangles are actually quadrilaterals, since each has four vertices and four edges.

Figure 77