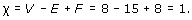4.3 The Euler characteristic
Subdivisions of surfaces lead to the third number used to classify surfaces, the Euler characteristic.
Definition
The Euler characteristic χ of a subdivision of a surface is
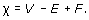
where V, E and F denote (respectively) the numbers of vertices, edges and faces in the subdivision.
Remark
The formula χ = V − E + F is often referred to as Euler's Formula.
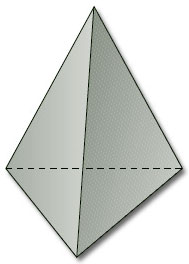
For example, the tetrahedron gives rise to a subdivision of the sphere where the vertices, edges and faces of the tetrahedron correspond to the vertices, edges and faces of the subdivision (Figure 86). This subdivision has 4 vertices, 6 edges and 4 faces, so its Euler characteristic is
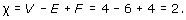
Similarly, the cube gives rise to a subdivision of the sphere (Figure 87).

This subdivision has 8 vertices, 12 edges and 6 faces, so its Euler characteristic is
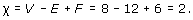
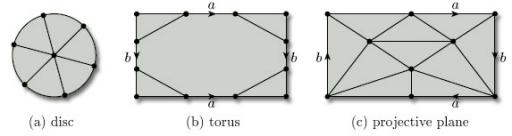
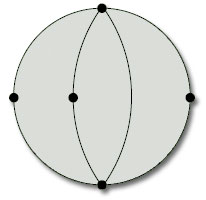
Figure 88 shows a subdivision of a closed disc, with 3 faces, 5 vertices and 7 edges. Its Euler characteristic is

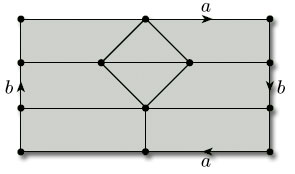
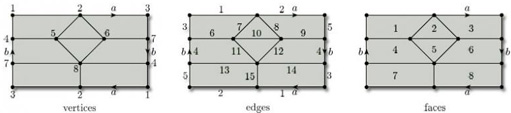
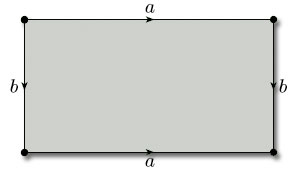
We saw in the last subsection that the rectangle with edge identifications that define a torus (Figure 89) represents a subdivision of the torus, with 1 vertex, 2 edges and 1 face. Its Euler characteristic is
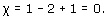
As the last example indicates, when we are dealing with a surface defined by a polygon with edge identifications, we need to be careful how we count the vertices, edges and faces. The following worked problem provides further illustration.
Worked problem 3
Problem 19
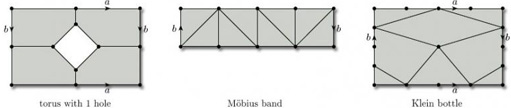
Find the Euler characteristic of each of the subdivisions in Figure 92: (a) torus with 1 hole, (b) Möbius band, (c) Klein bottle.
Answer
(a) This subdivision has 7 vertices, 12 edges, and 4 faces, so its Euler characteristic is
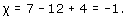
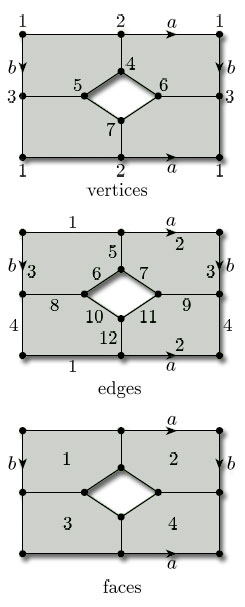
(b) This subdivision has 8 vertices, 16 edges, and 8 faces, so its Euler characteristic is
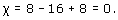
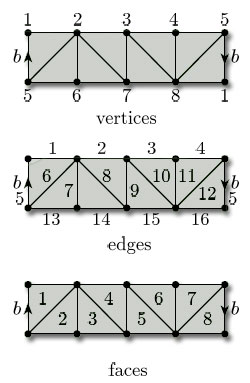
(c) This subdivision has 8 vertices, 16 edges, and 8 faces, so its Euler characteristic is
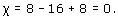
We have seen that the Euler characteristics of tetrahedral and cubic subdivisions of the sphere are equal to 2. More generally, it can be shown that the Euler characteristic is the same for any two subdivisions of the same surface. The proof of this general result is difficult, and so we simply state the result here.
Theorem 9
Any two subdivisions of the same surface have the same Euler characteristic.
For example, every subdivision of the sphere has Euler characteristic 2. Similarly, we have seen a subdivision of the torus with Euler characteristic 0: it follows that every subdivision of the torus has Euler characteristic 0.
Theorem 9 allows us to speak of the Euler characteristic of a surface, independently of the choice of subdivision, and to compute it using the most convenient subdivision.
Our assumption that the surface is compact guarantees that the Euler characteristic is always finite.
Definition
The Euler characteristic of a surface S is the Euler characteristic of any subdivision of S. It is denoted by χ(S).
(χ is the Greek letter chi.)
The earlier examples now enable us to conclude that the Euler characteristic of the sphere is 2, of the closed disc is 1, of the torus is 0, of the projective plane is 1, of the torus with 1 hole is −1, of the Möbius band is 0 and of the Klein bottle is 0.
Problem 20
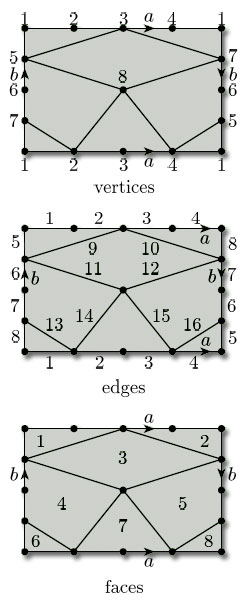
By considering the subdivisions in Figure 93, verify the Euler characteristic of each of the given surfaces.
Answer
(a) This subdivision has 7 vertices, 12 edges, and 6 faces, so the Euler characteristic is
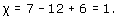
(b) This subdivision has 5 vertices, 10 edges, and 5 faces, so the Euler characteristic is
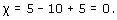
(c) This subdivision has 6 vertices, 15 edges, and 10 faces, so the Euler characteristic is
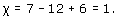
Problem 21
By drawing a suitable subdivision, find the Euler characteristic of a cylinder.
Answer
A simple subdivision is shown below. It has 2 vertices, 3 edges and 1 face, so the Euler characteristic is
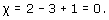

We conclude this subsection by remarking that any homeomorphism of a surface S onto a surface S' maps a subdivision of S onto a subdivision of S', sending the vertices of S to vertices of S', the edges of S to edges of S', and the faces of S to faces of S', in a one-to-one fashion. It follows that the value of V − E + F remains unchanged, and therefore that the Euler characteristic of a subdivision is preserved under homeomorphisms. Thus the Euler characteristic of a surface is a topological invariant.