4.5 Some general results
We next establish some general results about Euler characteristics. We start with a theorem that tells us what happens to the Euler characteristic of a surface when we remove an open disc.
Theorem 10: Disc Removal Theorem
The Euler characteristic of a surface with an open disc removed is one less than the Euler characteristic of the original surface.
Outline proof: Suppose that we are given a surface S containing an open disc. Any subdivision of S with the disc removed gives rise to a subdivision of S with the disc reinstated, as shown in Figure 94, and these two subdivisions have the same number V of vertices and the same number E of edges.
Recall that if a surface has a boundary then the boundary must consist of vertices and edges of the subdivision.
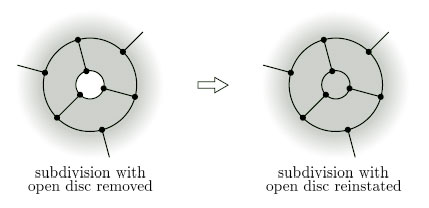
When we reinstate the disc, we increase F, the number of faces, by 1, while V and E are unchanged. So we increase the Euler characteristic χ = V − E +F by 1. It follows that the Euler characteristic of the surface with the disc removed is one less than the Euler characteristic of the original surface
The full proof is rather complicated, so we provide just an outline.
