5 Edge identifications
5.1 Identifying edges of a polygon
In this section, we revisit the construction of surfaces by identifying edges of polygons, as described in Section 2. Recall that, if we take any polygon in the plane and identify some of its edges in pairs, then we obtain a surface. When specifying how a given pair of edges is to be identified, we choose one of the two possible relative orientations of these edges.
In diagrams we represent such a rule for identifying edges by labelling the edges with letters and arrowheads, as in Figure 101: a pair of edges is identified if each carries the same letter, and the direction of identification is indicated by the arrowheads. We refer to an edge labelled with an arrowhead as a directed edge. Any assignment of letters and arrowheads to edges in which a particular letter appears on exactly two directed edges defines a rule for identifying edges of a polygon.
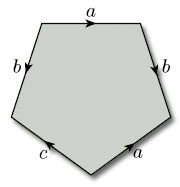
To prove that we do obtain a surface when we identify edges of a polygon in this way, we need to show how to make the resulting set into a topological space. We use a topology called the identification topology. We explore this topology and its consequences in this section.
