5.2 The identification topology

Our aim is to show that the object that we produce when we identify some or all the edges of a polygon is a surface. Therefore, by the definition of a surface given in Section 2.5, we must show how it can be given the structure of a topological space, and that this space is Hausdorff. Furthermore, we must show that every point has a disc-like or half-disc-like neighbourhood. We shall address the issue of showing that the object is a topological space in this subsection. We shall consider neighbourhoods and show that the space is Hausdorff in Section 5.3.

[ Its compactness and path-connectedness are guaranteed by its method of construction. ]

Our method for showing that the object is a topological space will be to construct a bijection between it and a known topological space. This will then allow us to define open sets for the object and hence show that it is a topological space.

The obvious known topological space is the polygon with edge identifications used to construct the object, since any polygon can be considered to have the subspace topology inherited from the Euclidean topology on ³. We also have a map from the polygon to the object, the map that takes points of the polygon to points of the object. Unfortunately, this map is not one-one, as it maps points on the edges to be identified to the same point on the object. However, we can turn this into a one-one map by creating what is known as the identification space of the polygon. Then, if we can show that this identification space is a topological space, we shall have essentially achieved our objective.

[ The map is onto. ]

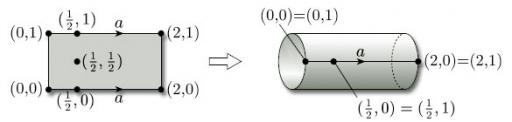
To define the identification space, we first need to define what we mean by an identification class. Consider the identification of opposite edges of a rectangle to form a cylinder, as illustrated in Figure 102.

Maximise

Figure 102

For each point x of the rectangle, we define the identification class of x to be the set of all points of the rectangle that are mapped to the same point of the cylinder as x is; for example, the class of (½, 0) consists of the pair of points (½, 0) and (½, 1), while the class of (½, ½) consists of just the point (½, ½). In general, we have the following definition:

Definition

Let f : X → Y be a function and let x X. The identification class of x, denoted by [x], is the set

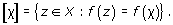
Worked problem 5

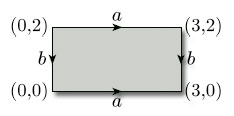
Consider the identification of opposite edges of the rectangle [0, 3] × [0, 2] to form a torus, as illustrated in Figure 103.

Figure 103

Write down the identification class [x] of each of the following points:

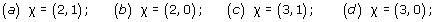
Solution

• (a)

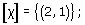
• (b)

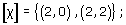
• (c)

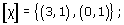
• (d)

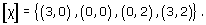
Problem 28

Consider the identification of opposite edges of the rectangle [0, 3] × [0, 2] to form a Klein bottle, as illustrated in Figure 104.

Figure 104

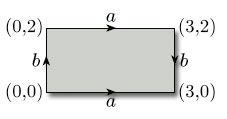
Write down the identification class [x] of each of the following points:

Answer

• (a)

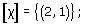
• (b)

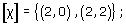
• (c)

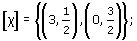
• (d)

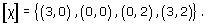
This now allows us to define the identification space of a polygon with edge identifications. In general the definition is as follows:

Let X be a polygon with edge identifications and let Y be the object obtained by making those edge identifications. Let f be the map that creates Y from X, so that f(X) = Y. We now use this map to create a bijection F from I(X) to Y, by letting F : I(X) → Y map the identification class [x] to the image point f(x), that is, F([x]) = f(x). This function is clearly onto. To show that it is one-one, we must show that if F([a]) = F([b]), then [a] = [b]. This follows since, if F([a]) = F([b]), then f(a) = f(b), and thus [a] = [b]. Thus F is a bijection, as required.

The next step is to define a topology on I(X). We first note that there is an obvious map p from X onto I(X), sending each element x to its identification class [x]. We now define a subset U of I(X) to be open if p⁻¹(U) is an open subset of X. This then creates the desired topology on I(X), as the following result demonstrates.