5.3.3 Torus with 1 hole
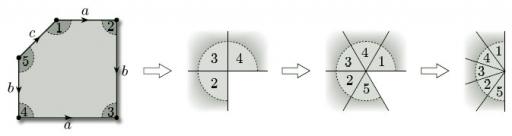
In our last example, we consider a pentagon with two pairs of edges identified. As we saw in Section 2.3, identification of the edges produces a torus with a hole. In this case there are five vertex-neighbourhoods to fit together, as shown in Figure 109. Identification of edges a and b shows that neighbourhoods 2, 3 and 4 fit together as shown. Identification of the edges b shows that neighbourhood 5 fits alongside neighbourhood 2, and identification of edges a shows that neighbourhood 1 fits alongside neighbourhood 4. However, neighbourhoods 1 and 5 do not fit together, and so we do not obtain a disc-like neighbourhood – rather we obtain a half-disc-like neighbourhood and the resulting vertex lies on the boundary of the hole.
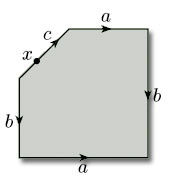
Finally consider a point x that lies on the edge c of the pentagon (see Figure 110). This has a half-disc-like neighbourhood. After identification of edges, this point lies on the boundary of the hole, and maintains its half-disc-like neighbourhood.
From these examples we can deduce that:
-
if a point lies on an edge that is identified with another edge, but not at a vertex of that edge, then after identification that point has a disc-like neighbourhood;
-
if a point lies on a part of the boundary that is not identified with another part, then after identification that point has a half-disc-like neighbourhood.
However, if a point is vertex of an edge that is identified with another edge, we have seen that after identification that point can have a disc-like or half-disc-like neighbourhood. We need to be sure that these are the only possibilities.
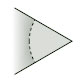
Consider the vertices x1, x2, …, xk of a polygon that are identified to the same point x by the edge identifications. In the polygon, each vertex xi has a half-disc-like neighbourhood that can be represented as in Figure 111. We shall call such a piece a wedge.
Some of the edges that come into each vertex xi are to be identified. Let us see what can happen. First, notice that the edge identifications that involve the vertices xi cannot have wedges that fit together to form two or more separate pieces: this is because, in such a case, the edge identifications would not identify all the vertices xi to a single point x. Also, because whole edges and not just vertices are identified, we cannot produce a situation such as that illustrated in Figure 112. Thus, the edge identifications that involve the vertices xi are such that all the wedges fit together to form a single neighbourhood. Either the point x is in the interior of the object so formed, as for the torus and Klein bottle, giving rise to a disc-like neighbourhood formed from the wedges, or the point x lies on the boundary, as for the torus with 1 hole. Thus:
-
if a point lies at a vertex of an edge that is identified with another edge, then after identification that point has a disc-like or half-disc-like neighbourhood.
We have therefore demonstrated that every point of polygon with edge identifications has, after identification, a disc-like or half-disc-like neighbourhood. Furthermore, given any two points of the object obtained after identification, by choosing disc-like or half-disc-like neighbourhoods of sufficiently small radius, we can find neighbourhoods that do not intersect – so the object is Hausdorff. Combining these results with those of Section 5.2 tells us that an object formed by identifying edges of a polygon is a surface, as defined in Section 2.5. Furthermore, we know that such a surface is homeomorphic to the identification space of the polygon with edge identifications.