8.1 W and Z bosons
In the same way that photons and gluons are the quanta involved in electromagnetic and strong interactions, respectively, weak interactions involve other quanta – known as W bosons and Z bosons.
In fact, there are two types of W boson, one with negative electric charge, the W− boson, and one with positive electric charge, the W+ boson. The two (charged) W bosons each have a mass of about 80 GeV/c2 whereas the (neutral) Z boson has a mass of about 90 GeV/c2. In weak interactions, W and Z bosons interact with each other, as well as with all quarks and leptons. The Universe would be an impossibly boring place without them.
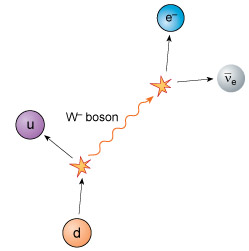
As you know, the beta-minus decay of a nucleus occurs when a neutron turns into a proton, with the emission of an electron and an electron antineutrino. At most, a few MeV of energy are released in this process, corresponding to the difference in mass between the original nucleus and the resultant nucleus. At the quark level, the explanation is that a down quark, d, with a negative electric charge equal to one-third that of an electron is transformed into an up quark, u, with a positive electric charge equal to two-thirds that of a proton.
A W− boson is emitted with one unit of negative electric charge, so conserving electric charge in the process. The mass energy of the W− boson is about 80 GeV, so it cannot possibly emerge from the nucleus as there are only a few MeV of energy available. In accordance with the energy–time uncertainty principle it therefore rapidly decays to produce an electron and an electron antineutrino, setting the energy accounts straight.
In weak interactions, the total number of quarks minus the total number of antiquarks is the same both before and after the interaction. The number of leptons is also conserved. In the example of beta-minus decay, there are no leptons initially present, and after the interaction there is one lepton and one antilepton – a net result of zero again.
This is the explanation for why neutrinos and antineutrinos are produced in beta-decays. If they were not, then the rule of lepton conservation would be violated. Notice also that the production of a charged lepton is always accompanied by the corresponding flavour of neutrino. In all weak interactions:
- electric charge is conserved
- the number of quarks minus the number of antiquarks is conserved
- the number of leptons minus the number of antileptons is conserved
- flavour changing of quarks or leptons is allowed, as long as these three rules are obeyed.
Following the example of beta-minus decay above, explain how beta-plus decay involves the creation and demise of a W+ boson. Check that electric charge is conserved, that the number of quarks minus the number of antiquarks is conserved, and that the number of leptons minus the number of antileptons is conserved.
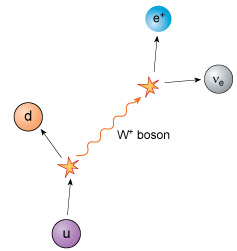Figure 9 A beta-plus decay process involves the creation and disappearance of a W+ boson. An up quark decays into a W+ boson and a down quark. The W+ boson subsequently decays into a positron and an electron neutrino.The electric charge is initially that of an up quark (). The products of the initial decay are a down quark with charge , and a W+ boson with charge +e, so charge is conserved here. The W+ boson subsequently decays into a positron with charge +e and a neutral electron neutrino, so charge is again conserved.
There is one quark present both before and after the decay, so the total number of quarks minus the number of antiquarks is conserved and equal to one. There are no leptons present initially, but one lepton (the electron neutrino) and one antilepton (the positron) are present at the end. Therefore, the total number of leptons minus the number of antileptons is also conserved and equal to zero.
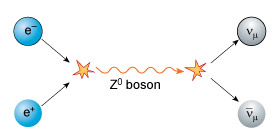
The third of the quanta involved in weak interactions is the Z0 boson with zero electric charge. An example of the type of reaction involving the Z0 boson is a collision between an electron and a positron. This can create a Z0 boson from the mass energy of the electron–positron pair, which subsequently decays into a muon neutrino and a muon antineutrino pair. Notice that there is one lepton and one antilepton both before and after the interaction.
