Course content Course content

Prices, location and spread

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3.2 Quartiles and the interquartile range

Finding the quartiles of a batch is very similar to finding the median.

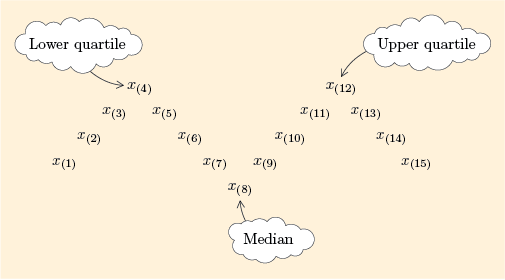
In Subsection 1.2, we represented a batch as a V-shaped formation, with the median at the ‘hinge’ where the two arms of the V meet. The median splits the batch into two equal parts. Similarly, we can put another hinge in each side of the V and get four roughly equal parts, shaped like this: . For a batch of size 15, it looks like Figure 12.

Figure 12 Median and quartiles

Show description|Hide description

An extended V-shaped diagram showing the median and quartiles. The V-shape has two additional arms, one to the left and one to the right, so the shape now resembles a capital letter M, but with the sides sloping. The numbers represented by x subscript 1, x subscript 2 and so on, ending with x subscript 15 are shown.

The shape starts on the left with x subscript 1, followed, slightly higher and to the right by x subscript 2. Following the same line are x subscript 3 and x subscript 4. At that point the V formation begins, so the next entry x subscript 5 is slightly lower down and to the right and level with x subscript 3. The same line is followed by x subscript 6, x subscript 7, which is level with x subscript 1, and x subscript 8, which is lower than x subscript 1. At x subscript 8 the direction changes again and the letters move slightly to the right and begin to rise, so x subscript 9 is level with x subscript 7. They continue to rise until x subscript 12 is reached. This is level with x subscript 4. The letters then begin to fall again, moving to the right each time, ending with x subscript 15. This is on the same horizontal level as x subscript 1.

There are three clouds, each containing words. The first contains the words ‘Lower quartile’ and has an arrow pointing to the label x subscript 4, which is at the top of the first line. To the right and at the same level is another cloud, containing the words ‘Upper quartile’, from which an arrow points to the label x subscript 12. The third cloud contains the word ‘Median’. From it an arrow points to the lowest label, x subscript 8, in the middle of the diagram.

Median and quartiles

The points at the side hinges, in this case and , are the quartiles. There are two quartiles which, as with the extremes, we call the lower quartile and the upper quartile. The lower quartile separates off the bottom quarter, or lowest 25%. The upper quartile separates off the top quarter, or highest 25%. They are denoted and respectively. (Sometimes they are referred to as the first quartile and the third quartile.)

You might be wondering, if these are and , what happened to ? Well, have a think about that for a moment.

separates the bottom quarter of the data (from the top three quarters), and separates the bottom three quarters (from the top quarter). So it would make sense to say that separates the bottom two quarters (from the top two quarters). But two quarters make a half, so would denote the median, and since there is already a separate word for that, it’s not usual to call it the second quartile.

Usually we cannot divide the batch exactly into quarters. Indeed, this is illustrated in Figure 12 where the two central parts of the are larger than the outer ones. As with calculating the median for an even-sized batch, some rule is needed to tell us how many places we need to count along from the smallest value to find the quartiles. However, there are several alternatives that we could adopt and the particular rule described below is somewhat arbitrary. Different authors and different software may use slightly different rules. If your calculator can find quartiles, note that it may use a different rule.

As you might have expected, the rule involves dividing by 4, where is the batch size (as opposed to dividing by 2 to find the median). However, the rule is slightly more complicated for the quartiles and it depends on whether is exactly divisible by 4.

The quartiles

The lower quartile is at position in the ordered batch.

The upper quartile is at position in the ordered batch.

If is exactly divisible by 4, these positions correspond to a single value in the batch.

If is not exactly divisible by 4, then the positions are to be interpreted as follows.

A position which is a whole number followed by means ‘halfway between the two positions either side’ (as was the case for finding the median).
A position which is a whole number followed by means ‘one quarter of the way from the position below to the position above’. So for instance if a position is , the quartile is the number one quarter of the way from to .
A position which is a whole number followed by means ‘three quarters of the way from the position below to the position above’. So for instance if a position is , the quartile is the number three quarters of the way from to .

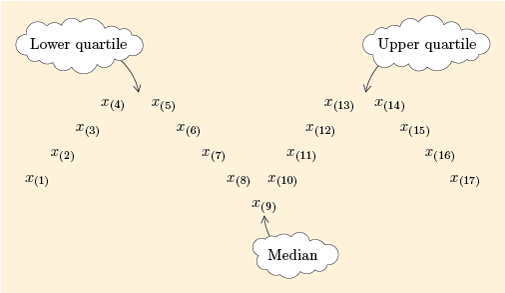
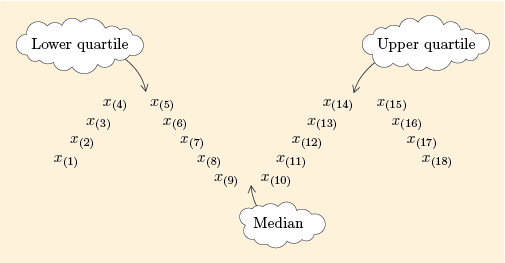
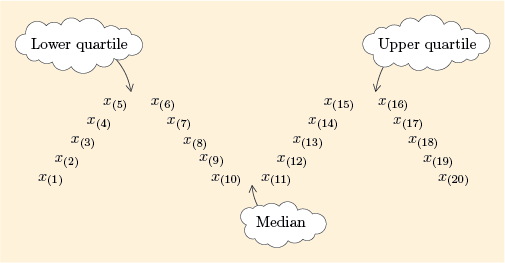
Before we actually use these rules to find quartiles, let us look at some more examples of -shaped diagrams for different batch sizes . The case where is exactly divisible by 4, so that is a whole number, was shown in Figure 12. The following three figures show the three other possible scenarios, where is not exactly divisible by 4.

For , and . So is halfway between and , and is halfway between and .

Figure 13 Quartiles for sample size

Show description|Hide description

Diagram showing the quartiles for sample size n = 17. The V-shape has two additional arms, one to the left and one to the right, so the shape now resembles a capital letter M, but with the sides sloping. The numbers represented by x subscript 1, x subscript 2 and so on, ending with x subscript 17 are shown.

The shape starts on the left with x subscript 1, followed, slightly higher and to the right by x subscript 2, Following the same line are x subscript 3 and x subscript 4. At that point the V formation begins, but there is a gap at the top. The next entry x subscript 5 is level with but to the right of x subscript 4. The same line is followed by x subscript 6, x subscript 7 and x subscript 8, which is level with x subscript 1. Continuing in the same direction leads to x subscript 9, which is at a lower level than x subscript 1. At x subscript 9 the direction changes again and the letters begin to rise, moving slightly to the right again until x subscript 13 is reached. This is level with x subscript 5. X subscript 14 is to the right of and level with x subscript 13 and forms the start of the last slope. The letters then begin to fall again, moving to the right each time, ending with x subscript 17. This is on the same horizontal level as x subscript 1.

There are three clouds, each containing words. The first contains the words ‘Lower quartile’ and has an arrow pointing to the gap between x subscript 4 and x subscript 5. To the right and at the same level is another cloud, containing the words ‘Upper quartile’, from which an arrow points to the gap between x subscript 13 and x subscript 14. The third cloud contains the word ‘Median’. From it an arrow points to the lowest label, x subscript 9, in the middle of the diagram.

Quartiles for sample size MathJax failure: MathML - Unexpected text node: '

For , and . So is three quarters of the way from to , and is one quarter of the way from to .

Figure 14 Quartiles for sample size

Show description|Hide description

Diagram showing the quartiles for sample size n = 18. The V-shape has two additional arms, one to the left and one to the right, so the shape now resembles a capital letter M, but with the sides sloping. The numbers represented by x subscript 1, x subscript 2 and so on, ending with x subscript 18 are shown.

The shape starts on the left with x subscript 1, followed, slightly higher and to the right by x subscript 2, Following the same line are x subscript 3 and x subscript 4. At that point the V formation begins, but there is a gap at the top. The next entry x subscript 5 is level with but to the right of x subscript 4. The same line is followed by x subscript 6, x subscript 7 and x subscript 8, which is level with x subscript 1. Continuing in the same direction leads to x subscript 9, which is at a lower level than x subscript 1. At x subscript 9 there is a gap. The direction changes again and the letters begin to rise. Slightly to the right but level with x subscript 9 is x subscript 10. They continue to rise and move to the right until x subscript 14 is reached. This is level with x subscript 5. There is then a gap and the letters then begin to fall again, starting with x subscript 15 which is level with x subscript 14. They continue down, moving to the right each time, ending with x subscript 18. This is on the same horizontal level as x subscript 1.

There are three clouds, each containing words. The first contains the words ‘Lower quartile’ and has an arrow pointing to the gap between x subscript 4 and x subscript 5 with the arrowhead closer to x subscript 5 than x subscript 4. To the right and at the same level is another cloud, containing the words ‘Upper quartile’, from which an arrow points to the gap between x subscript 14 and x subscript 15 with the arrowhead closer to x subscript 14 than x subscript 15. Below the diagram a third cloud contains the word ‘Median’. From it an arrow points to the gap between x subscript 9 and x subscript 10, in the middle of the diagram.

Quartiles for sample size MathJax failure: MathML - Unexpected text node: '

For , and . So is one quarter of the way from to , and is three quarters of the way from to .

Figure 15 Quartiles for sample size

Show description|Hide description

Diagram showing the quartiles for sample size n = 20. The V-shape has two additional arms, one to the left and one to the right, so the shape now resembles a capital letter M, but with the sides sloping. The numbers represented by x subscript 1, x subscript 2 and so on, ending with x subscript 20 are shown.

The shape starts with x subscript 1, followed, slightly higher and to the right by x subscript 2, Following the same line are x subscript 3, x subscript 4 and x subscript 5. At that point the V formation begins, but there is a gap at the top. The next entry x subscript 6 is level with but to the right of x subscript 5. The same line is followed by x subscript 7, x subscript 8, x subscript 9 and x subscript 10, which is level with x subscript 1. At x subscript 10 there is a gap. The direction changes again and the letters begin to rise. Slightly to the right but level with x subscript 10 is x subscript 11. The letters continue to rise and move to the right until x subscript 15 is reached. This is level with x subscript 6. There is then a gap and the letters move to the right and begin to fall again, starting with x subscript 16 which is level with x subscript 15. They continue down, moving to the right each time, ending with x subscript 20. This is on the same horizontal level as x subscript 11.

There are three clouds, each containing words. Above the diagram the first cloud contains the words ‘Lower quartile’ and has an arrow pointing to the gap between x subscript 5 and x subscript 6 with the arrowhead closer to x subscript 5 than x subscript 6. To the right and at the same level is another cloud, containing the words ‘Upper quartile’, from which an arrow points to the gap between x subscript 15 and x subscript 16 with the arrowhead closer to x subscript 16 than x subscript 15. The third cloud is below the diagram and contains the word ‘Median’. From it an arrow points to the gap between x subscript 10 and x subscript 11, in the middle of the diagram.

Quartiles for sample size MathJax failure: MathML - Unexpected text node: '

Example 14 Quartiles for the prices of small televisions

Figure 15 showed you where the quartiles are for a batch of size 20. Let us now use the stemplot of the 20 television prices in Figure 16, which you first met in Figure 5 (Subsection 1.2), to find the lower and upper quartiles, and , of this batch.

Figure 16 Prices of flat-screen televisions with a screen size of 24 inches or less

Show description|Hide description

Stemplot with 10 levels, though there are repeated numbers in the stem. The numbers in the stem are 0, 1, 1, 1, 1, 1, 2, 2, 2, 2. At level 0 there is one leaf 9. At the first level 1 there is one leaf, 0. At the second level 1 there are four leaves 2, 3, 3, 3. The third level 1 has five leaves, 4, 5, 5, 5, 5. The fourth level 1 has three leaves, 6, 6, 7. The fifth and last level 1 has three leaves, 8, 8, 9. The first level 2 and the second level 2 have no leaves. The third level 2 has two leaves, 4, 5. The last level 2 has one leaf, 7. Beneath the stemplot is written n = 20, followed by 0 vertical line 9 represents 90 pounds sterling. The vertical line sits horizontally between the 0 and the 9.

Prices of flat-screen televisions with a screen size of 24 inches or less

To calculate the lower quartile you need to find the number that is one quarter of the way from to . These values are both 130, so is 130. To calculate the upper quartile you need to find the number three quarters of the way from to . These values are both 180, so is 180.

That example was easier than it might have been, because for each quartile the two numbers we had to consider turned out to be equal!

Example 15 Quartiles for the camera prices

Table 2 (Subsection 1.2) gave ten prices for a particular model of digital camera (in pounds). In order, the prices are as follows.

To find the lower and upper quartiles, and , of this batch, first find and .

The lower quartile is the number three quarters of the way from to . These values are 60 and 65. The difference between them is , and three quarters of that difference is . Therefore is 3.75 larger than 60, so it is 63.75. As with the median, in this course we will generally round the quartiles to the accuracy of the original data, so in this case we round to the nearest whole number, 64. In symbols, .

The upper quartile is the number one quarter of the way from to . These values are 81 and 85. The difference between them is , and one quarter of that difference is . Therefore is 1 larger than 81, so it is 82. (No rounding necessary this time.) In symbols, .

Example 15 is the subject of the following screencast. [Note that references to ‘the unit’ should be interpreted as ‘this course’. The original wording refers to the Open University course from which this material is adapted.]

Download this video clip.Video player: Calculating quartiles

Show transcript|Hide transcript

Transcript: Screencast 3 Calculating quartiles

INSTRUCTOR

Here’s another batch of data from the unit. This time, it’s the prices of a particular model of digital camera. And there are the prices along the top in pounds. And what we’re asked to do is to find the lower and upper quartiles of this batch of data.

So usually the first thing you have to do when you’re finding the median or the lower and upper quartiles is to put the prices in order. But if you have a look up at the top there, luckily, somebody’s already done that for us. They’re in order.

So we can bash straight on with the next step, which is actually finding the quartiles. Now, what I’m going to do to begin with is to use the notation that we use in defining what the quartiles are, just so you can relate what I’m doing to what’s in the unit on that. Remember how that works. We take the first number, the smallest number in the batch, which in this case is 53, right over the left there.

And we write that as x, within brackets, 1. The 1 in brackets means it’s the smallest value in the batch. And the next one, which is 60, that’s x, brackets, 2. And then you just carry on like that.

And the last one is x10. That means there’s 10 values in this bunch. We need to know that.

And in fact, that’s the next thing we need to worry about. There are 10 observations, 10 camera prices. So in the notation, we call that n. n’s 10.

Now, remember what you’ve got to do to work out this. We want for the quartiles a number that’s 1/4 of the way along the batch when we’ve arranged it in order and another number that’s 3/4 of the way along the batch. But of course, it’s a bit more complicated than that. You don’t look at 1/4 of n. You look at n plus 1 divided by 4.

And that gives you the position of the lower quartiles. n plus 1 divided by 4 is 11/4, which is 2 and 3/4. And that defines where the position of the lower quartile is in a way that I’ll come to.

And to get the upper quartile – well, this time, you’ve got to take 3/4 of n plus 1. That is 3 times n plus 1, over 4. And that comes to n plus 1 is 11.

So it’s 33 – 3 times 11 – over 4. And if you work that out, that’s 8 and 1/4. And that defines the position of the upper quartile.

OK, so moving on, then, Q1 is the lower quartile. And it’s defined by this number here, this 2 and 3/4 number. And what that tells us is it’s between the second number in order and the third number. And it’s 3/4 of the way between them.

So I’ll just write down what that is. Q1 is 3/4 of the way from x2 to x3. And you can work that out just in arithmetic – but it’s probably easier if we have a look and see what it looks like graphically.

Here is a bit of a number line. x2 is going to be there. And x2 is 60.

And x3’s going to be up here somewhere. And x3, if we look up here, is 65. So that one’s 65.

And what we want is a number that’s 3/4 of the way from 60 to 65. Well, that’s halfway there. That’s going to be 62 and 1/2. And 3/4 of the way is about here somewhere. And that’s going to be 63.75.

OK, but how do we write that down in algebra? The way to do it is like this. We say you start at x2, which is 60. And then you go 3/4 of the way from x2 to x3.

Well, how far is it from x2 to x3? Well, again, if you look on this, it’s 65 to 60. That is 5.

And you can calculate that as 65 minus 60. So it’s 3/4 of 65 minus 60. So that’s 60 plus – we’ve got 3 times 5 over 4. That is 15/4. And if you work that out on your calculator or something, it comes to 63.75.

So we’ve worked out the lower quartile. It’s 63.75. And luckily, that’s the same as I showed you over here.

So now we’ve got to go and find the upper quartile. Remember, we denote that as Q3. And if you look at the thing over here, that says it’s at position 8 and 1/4, which means it’s 1/4 of the way from the eighth one to the ninth one. That is, it is 1/4 of the way from x8 to x9.

And again, it’s helpful to draw what’s going on here. So here is a number line. And here we’ve got x8, which is 81. And here we’ve got x9, which is 85.

And again, we want the number that’s 1/4 of the way along, bit different. So here’s halfway. That’s going to be 83. And here is 1/4 of the way, halfway between 81 and 83. That’s 82.

So it’s going to be 82. Let’s just see how we can write that down as a bit of algebra. So again, you start from x8, which is 81. And then you go 1/4 of the way up to x9.

Now this time, the distance between x8 and x9 is 85 – that’s x9 – minus 81, which is x8. So the arithmetic’s actually a lot easier in this case. That’s 81 plus 1/4 of 4. And that just comes to 81 plus 1, which is 82. Again, it’s the same.

So just one final step to do here. We’ve got to write down the answers in an appropriate way. Now, what we have to do is round them to an appropriate accuracy. That’s all we haven’t done.

And what we’ve got is that Q1 – what accuracy do we use? Well, the usual thing we do is to round quartiles to the accuracy of the original data that we had. And the original data we had up at the top there is in whole pounds. It’s rounded to whole pounds. So we need the quartiles in whole pounds, as well.

And if you look at this one, it’s not in whole pounds. It’s 63.75. So we’ve got to round it to the nearest pound. The bit in pence, essentially, here that we’re going to get rid of in the rounding is bigger than 1/2.

So we’ve got to round up. That is, this one is– let’s write in the pound sign. It’s £64 to the nearest pound.

And what about Q3? Well, you’ve got to think about rounding that, as well. But actually, you needn’t bother. It’s already a whole number of pounds, so no rounding involved. We can just write down it’s 82. And that’s that.

End transcript: Screencast 3 Calculating quartiles

Download

Screencast 3 Calculating quartiles

Interactive feature not available in single page view (see it in standard view).

Activity 10 Finding more quartiles

(a) Find the lower and upper quartiles of the batch of 15 coffee prices in Figure 17. (This batch of coffee prices was first introduced in Table 1 of Subsection 1.1.)

Figure 17 Stemplot of 15 coffee prices

Show description|Hide description

A stemplot with 11 levels, which start at 26 and end at 36. At level 26 there are five leaves 8, 8, 8, 8, 9. At level 27 there two leaves 5, 9. At level 28 there are no leaves. Level 29 has five leaves, 5, 5, 5, 5, 9. Level 30 has one leaf, 5 and level 31 also has one leaf, 5. Levels 32, 33, 34, and 35 have no leaves. Level 36 has one leaf, 9. Beneath the stemplot is written n = 15, followed by 26 vertical line 8 represents 268 pence. The vertical line sits horizontally between the 26 and the 8.

Stemplot of 15 coffee prices

Discussion

Here, because , an appropriate picture of the data would be Figure 12 (Subsection 3.2). To find the lower and upper quartiles, and , of this batch, first find and . Therefore and .

(b) Find the lower and upper quartiles of the batch of 14 gas prices in Figure 18. (This batch of gas prices was first introduced in Table 3 of Subsection 1.2.)

Figure 18 Stemplot of 14 gas prices

Show description|Hide description

A stemplot with 8 levels, which start at 374 and end at 381. Level 374 has three leaves, 0, 0, 3. Level 375 has no leaves. Level 376 has two leaves, 0, 7. Level 377 has one leaf, 6. Level 378 also has one leaf, 4. Level 379 has two leaves, 5, 6. Level 380 has four leaves, 1, 1, 4, 5. Level 381 has one leaf, 8. Beneath the stemplot is written n = 14, followed by 374 vertical line 0 represents 3.740 pence per kilowatt hour. The vertical line sits horizontally between the 374 and the 0.

Stemplot of 14 gas prices

Discussion

For this batch, so and .

and

So the lower quartile is 3.756 p per kWh and the upper quartile is 3.802p per kWh.

Previous 3.1 The range

Next A measure of spread

Take your learning further

Making the decision to study can be a big step, which is why you’ll want a trusted University. We’ve pioneered distance learning for over 50 years, bringing university to you wherever you are so you can fit study around your life. Take a look at all Open University courses.

If you’re new to university-level study, read our guide on Where to take your learning next, or find out more about the types of qualifications we offer including entry level Access modules, Certificates, and Short Courses.

Want to achieve your ambition? Study with us and you’ll be joining over 2 million students who’ve achieved their career and personal goals with The Open University.

Browse all Open University courses

My OpenLearn Profile

About this free course

Become an OU student

Download this course

Share this free course

3.2 Quartiles and the interquartile range

The quartiles

Example 14 Quartiles for the prices of small televisions

Example 15 Quartiles for the camera prices

Transcript: Screencast 3 Calculating quartiles

Activity 10 Finding more quartiles

Discussion

Discussion