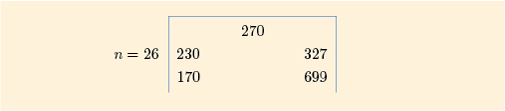Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Prices, location and spread
Prices, location and spread

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

Exercises on Section 3

The following exercises provide extra practice on the topics covered in Section 3.

Exercise 6 Finding quartiles and the interquartile range

(a) For the arithmetic scores in Exercise 1 (Section 1), find the quartiles and calculate the interquartile range. The stemplot of the scores is given below.

Described image
Figure 30 Stemplot of arithmetic stores
Show description|Hide description

A stemplot with 11 levels. The numbers in the stem start at 0, increase in steps of one and end at 10. At level 0 there is one leaf, 7. Level 1 has one leaf, 5. Level 2 has no leaves, while level 3 has two leaves, 3, 5. Level 4 has three leaves, 2, 2, 3. Level 5 has two leaves, 5, 8. Level 6 has three leaves, 4, 6, 8. Level 7 has five leaves, 1, 1, 6, 8, 9. Level 8 has nine leaves, 0, 1, 1, 3, 4, 5, 5, 6, 9. Level 9 has five leaves, 1, 1, 3, 5, 9. Level 10 has two leaves which are both 0. Beneath the stemplot is written n = 33, followed by 0 vertical line 7 represents a score of 7 per cent.

Figure 30 Stemplot of arithmetic stores

Discussion

For the arithmetic scores, n=33 so fraction 1 over 4 end open bracket n+1 close bracket = 8 fraction 1 over 2 end and fraction 3 over 4 end open bracket n+1 close bracket = 25 fraction 1 over 2 end.

The lower quartile is therefore

uppercase Q sub 1 = fraction 1 over 2 end open bracket 55+58 close bracket % = 56.5 % simeq 57 % .

The upper quartile is

uppercase Q sub 3 = fraction 1 over 2 end open bracket 86+89 close bracket % = 87.5 % simeq 88 % .

The interquartile range is

uppercase Q sub 3 minus uppercase Q sub 1 = 87.5 % minus 56.5 % = 31 % .

(b) For the television prices in Exercise 1, find the quartiles and calculate the interquartile range. The table of prices is given below.

170

180

190

200

220

229

230

230

230

230

250

269

269

270

279

299

300

300

315

320

349

350

400

429

649

699

Discussion

For the television prices, n=26 so fraction 1 over 4 end open bracket n+1 close bracket = 6 fraction 3 over 4 end and fraction 3 over 4 end open bracket n+1 close bracket = 20 fraction 1 over 4 end.

The lower quartile is therefore

uppercase Q sub 1 = pounds 229 + fraction 3 over 4 end open bracket pounds 230 minus pounds 229 close bracket = pounds 229.75 simeq pounds 230.

The upper quartile is

uppercase Q sub 3 = pounds 320 + fraction 1 over 4 end open bracket pounds 349 minus pounds 320 close bracket = pounds 327.25 simeq pounds 327.

The interquartile range is

uppercase Q sub 3 minus uppercase Q sub 1 = pounds 327.25 minus pounds 229.75 = pounds 97.5 simeq pounds 98.

Exercise 7 Some five-figure summaries

Prepare a five-figure summary for each of the two batches from Exercise 1.

(a) For the arithmetic scores, the median is 79% (found in Exercise 1), and you found the quartiles and interquartile range in Exercise 6.

Discussion

Arithmetic scores:

From the stemplot, n=33, uppercase E subscript uppercase L end = 7 and uppercase E subscript uppercase U end = 100.

Described image
Figure 31 Five-figure summary of arithmetic scores
Show description|Hide description

A five-figure summary. The diagram forms three sides of a rectangle, with the bottom line missing. It therefore has a vertical line to the left, a horizontal line across the top and a vertical line to the right. To the left of the left vertical line is written n = 33. Towards the bottom of the line and to its right is written 7 and above that 57. Beneath the middle of the horizontal line is written 79. To the left of the second vertical line and level with 57 is written 88. Below that and level with 7 is written 100.

Five-figure summary of arithmetic scores

(b) For the television prices, the median is £270 (found in Exercise 1), and you found the quartiles and interquartile range in Exercise 6.

Discussion

Television prices:

From the data table, n=26, uppercase E subscript uppercase L end = 170 and uppercase E subscript uppercase U end = 699.

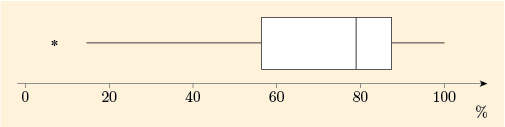
Described image
Figure 32 Five-figure summary of television prices
Show description|Hide description

A five-figure summary. The diagram forms three sides of a rectangle, with the bottom line missing. It therefore has a vertical line to the left, a horizontal line across the top and a vertical line to the right. To the left of the left vertical line is written n = 26. Towards the bottom of the line and to its right is written 170 and above that 230. Beneath the middle of the horizontal line is written 270. To the left of the second vertical line and level with 230 is written 327. Below that and level with 170 is written 699.

Five-figure summary of television prices

Exercise 8 Boxplots and the shape of distributions

Boxplots of the two batches used in Exercises 1, 6 and 7 are shown in Figures 33 and 34. On the basis of these diagrams, comment on the symmetry and/or skewness of these data.

Described image
Figure 33 Boxplot of batch of 33 arithmetic scores
Show description|Hide description

A boxplot of a batch of 33 arithmetic scores. There is a horizontal scale with an arrow head, pointing right, at the right-hand end. It is labelled percentage. The scale starts at 0 and is then marked in five intervals of 20, ending with 100. Above the line, and level with the boxplot is an asterisk at 7. The first whisker on the boxplot starts at 15. The capital Q subscript 1 is at about 58, capital M is at about 79 and capital Q subscript 3 is at about 86. The second whisker stretches to the upper extreme at 100.

Boxplot of batch of 33 arithmetic scores
Described image
Figure 34 Boxplot of batch of 26 television prices
Show description|Hide description

A boxplot of a batch of 26 television prices. There is a horizontal scale with an arrow head, pointing right, at the right-hand end. It is labelled pounds sterling. The scale starts at 100 and is then marked in six intervals of 100, ending with 700. The first whisker on the boxplot starts at 170. The box starts at capital Q subscript 1, which is about 230 and capital M is at about 270. The box ends at capital Q subscript 3 at about 320. The second whisker ends at 429. There are two asterisks. One is at 649 and the other is at 699.

Boxplot of batch of 26 television prices

Discussion

For the boxplot of arithmetic scores, the left part of the box is longer than the right part, and the left whisker is also considerably longer than the right. This batch is left-skew.

For the boxplot of television prices, the right part of the box is rather longer than the left part. The right whisker is also rather longer than the left, and if one also takes into account the fact that two potential outliers have been marked, the top 25% of the data are clearly much more spread out than the bottom 25%. This batch is right-skew.