2.5.2 Quantum fields and unification
From its inception, quantum physics was concerned not just with particles such as electrons, but also with light and other forms of electromagnetic radiation. In 1900 Planck discovered the quantum in the transfer of energy from matter to radiation, and in 1905, Einstein's explanation of the photoelectric effect assumed that the transfer of energy from radiation to matter occurred in a similarly quantised fashion. It is therefore hardly surprising that the development of quantum mechanics was soon followed by an attempt to formulate a quantum theory of electromagnetic radiation. That meant, of course, combining quantum ideas such as Planck's constant and intrinsic probabilities with the field theory of electromagnetism. The result would be a quantum field theory.
The quantum field theory of electromagnetism is called quantum electrodynamics, or QED for short. Its formulation proved to be very difficult. The first steps were taken by the British physicist Paul Dirac in 1927, but the theory was not really sorted out until the late 1940s.
Paul Adrien Maurice Dirac (1902-1984)

Paul Adrien Maurice Dirac was born in Bristol, England, in 1902. His father was a Swiss-born teacher of French, his mother a librarian. Dirac's first degree, obtained at the Merchant Venturer's Technical College, was in electrical engineering, but he had no real interest in the subject and after graduating spent two years studying mathematics at the University of Bristol. In 1923 he left Bristol for Cambridge where he remained for most of his working life.
Dirac's achievements in Cambridge were prodigious. In 1925, while working for his doctorate, he became one of the founders of quantum mechanics when he produced an elegant extension of Heisenberg's work. A little over a year later he presented a very general formulation of quantum mechanics that has remained the basis of the subject ever since. During the next year he essentially founded quantum electrodynamics. In 1928 Dirac took an important step towards bringing quantum physics into conformity with Einstein's special theory of relativity by devising an equation (now called the Dirac equation) that could describe the behaviour of electrons at any speed up to the speed of light. This equation provided a natural explanation of one of the electron's intrinsic properties - its spin. Taking the mathematical form of his equation seriously, and searching for a way of interpreting it, Dirac was led, in 1931, to propose that there should exist a class of 'anti-electrons', particles with the same mass and spin as the electron but with the opposite electrical charge (Figure 34). By correctly predicting the existence of these antiparticles, now called positrons, Dirac became recognised as the 'discoverer' of antimatter - one of the most important discoveries of the century.
From 1932 to 1969 Dirac held the Lucasian Chair of Mathematics in Cambridge, the post that Newton himself had once occupied. During this period Dirac worked on a variety of topics including magnetic monopoles (hypothetical magnetic charges) and the speculation that the fundamental constants of physics might be gradually changing in a co-ordinated way. However he became disenchanted with some of the detailed developments that occurred in quantum field theory and became increasingly distanced from what others regarded as the scientific mainstream.
In 1971, following his retirement from Cambridge, Dirac moved to the USA where he became a professor of physics at Florida State University. He died there in 1984. Throughout his life Dirac was renowned for his economy of speech and lack of social awareness. His book Principles of Quantum Mechanics (1930) is regarded as a classic of clear and elegant exposition. When a correspondent asked him to clarify a certain result in the text, Dirac is said to have replied that he knew of no clearer way of expressing the point. No rudeness would have been intended, just an honest statement of fact. Dirac preferred to work by himself, and had few collaborators or research students.

During the lengthy development of QED the following important features of quantum field theory became apparent.
Quantum field theory provides the natural way of combining special relativity and quantum physics. Quantum mechanics, as originally formulated by Heisenberg and Schrödinger, was inconsistent with the principle of relativity. Attempts were made to rectify this problem and significant progress was made by Dirac with his relativistic electron equation. However, despite many successes it became increasingly clear that relativistic quantum mechanics was ultimately self-contradictory and that quantum field theory provided the natural way of producing a relativistic quantum physics.
Quantum fields may be regarded as collections of particles. In the case of the quantised electromagnetic field these particles are called photons. Each photon of a particular colour carries a characteristic amount of energy: the quantum of energy used by Planck and Einstein. Emission and absorption of radiation corresponds to the creation and destruction of photons and therefore inevitably involves the transfer of complete quanta of energy. (Interestingly, Einstein realised as early as 1905 that the quantised transfer of energy would be explained if radiation actually consisted of particles, but the idea was not well received and he did not press it. Photons only became an accepted part of physics in the 1920s.)
Quantum field theory can be used to describe all fundamental particles. Electrons and positrons are normally regarded as examples of fundamental particles of matter. In quantum field theory all such particles are associated with quantum fields in much the same way that photons are associated with the electromagnetic field. The number of particles of a given type reflects the state of excitation of the field, and the particles are said to be 'quanta of excitation' of the field. Thus, although quantum field theory describes particles and the forces between them, it does so entirely in terms of quantum fields.
Quantum field theory describes processes in which particles are created or destroyed. When a quantum field becomes more excited, the number of quanta of excitation increases. This occurs because new particle-antiparticle pairs are created from radiation. When a quantum field becomes less excited, the number of quanta of excitation decreases. This is achieved by processes in which particles and antiparticles collide and annihilate one another to produce radiation. (Both of these processes are permitted by Einstein's E = mc2, and were explicitly predicted by Dirac.)
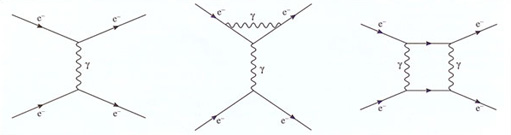
These were all very attractive features of quantum field theory and raised the hope that it might be a truly fundamental theory capable of providing a new world-view. However, there were serious problems within quantum electrodynamics that had to be overcome before such hopes stood any chance of being realised. Using QED to predict the value of a physically measurable quantity involved, in practice, working out the contribution made by several different sub-processes. Making sure that these sub-processes were fully identified was a problem in itself, working out their individual contributions was even worse. Even in the simplest cases, determining the contributions was difficult, and in the more complicated cases the result was usually a meaningless infinity showing that something was wrong. It was the problem of infinities that really delayed the completion of QED until the late 1940s. At that time, in a burst of post-war activity, a technique called renormalisation was developed that made it possible to get at the physical result hidden behind the unphysical infinity. At the same time a simple diagrammatic method was devised that made it much easier to identify and perform the necessary calculations. The problem of infinities was solved by Julian Schwinger (1918-1994), Sin-itiro Tomonaga (1906-1979) and Richard P. Feynman. The last of these was also responsible for the diagrams, which have become known as Feynman diagrams (Figure 35).