Numbers
| Site: | OpenLearn Create |
| Course: | Number confidence for work |
| Book: | Numbers |
| Printed by: | Guest user |
| Date: | Sunday, 30 November 2025, 12:51 PM |
1. Numbers
Having ten digits, five on each hand, seems like a good reason to count, as we do, in multiples of ten, and did you know that digit is another word for number?
Numbers can be positive (greater than 0), for example, 3 (three, or plus 3) or negative (less than 0) for example -3 (minus 3).

Our 'Base 10' system uses ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), combined with place values, to represent any number.
1.1. Positive and negative numbers
Positive numbers are greater than 0, for example 3 (3, or plus 3).
Negative numbers are less than 0, for example -3 (minus 3).
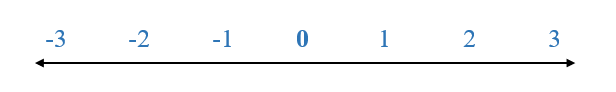
Everyday situations where both positive and negative values are frequently used include:
- Recording temperature: minus (below zero) temperatures are colder, and plus (above zero) temperatures are warmer.
- Money management: a plus (above zero) balance on your bank statement is money you have, whereas a minus balance (less than zero) could indicate money you owe.
1.2. Whole numbers and place value
Whole numbers are positive numbers (upwards from and including 0), which have no decimal or fractional elements. For example: 0, 5, 13, 128.
The number of digits used, and the place value of each, tells us the value of that number.
A table with appropriate headings can be a useful aid to understanding place values.
Starting on the right, and working from right to left, the headings in this table represent units (U), Tens (T), Hundreds (H), Thousands (Th), Ten-Thousands (TTh), Hundred-Thousands (HTh) and Millions (M).
| M | HTh | TTh | Th | H | T | U |
|---|---|---|---|---|---|---|
| 1 | 0 | |||||
| 2 | 6 | |||||
| 3 | 4 | |||||
| 1 | 0 | 0 | ||||
| 4 | 6 | 0 | ||||
| 1 | 0 | 2 | 2 | |||
| 4 | 2 | 6 | 5 | 0 | ||
| 3 | 4 | 0 | 5 | 4 | 6 | |
| 2 | 6 | 3 | 2 | 0 | 0 | 0 |
Units
A single digit is used to represent a value from 0 (zero) to 9 (nine).
Tens
Two digits are used to represent values from 10 (ten) to 99 (ninety-nine), with the digit on the right representing units and the digit to its left representing multiples of ten.
- 10 (ten): 1 ten and 0 units
- 26 (twenty-six): 2 tens and 6 units
- 34 (thirty-four): 3 tens and 4 units
Hundreds
Three digits are used to represent values from 100 (one hundred) to 999 (nine-hundred and ninety-nine), with the place values from left to right representing hundreds, tens and units.
- 100 (a hundred): 1 hundred, 0 tens and 0 units
- 460 (four hundred and sixty): 4 hundreds, 6 tens and 0 units
Larger numbers
Using further digits, we can represent increasingly larger values.
- 1 022 (One thousand and twenty-two): 1 thousand, 0 hundreds, 2 tens and 2 units
- 42 650 (forty-two thousand, six hundred and fifty): 4 ten-thousands, 2 thousands, 6 hundreds, 5 tens and 0 units
- 340 546 (three hundred and forty thousand, five hundred and forty-six): 3 hundred-thousands, 4 ten-thousands, 0 thousands, 5 hundreds, 4 tens and 6 units
- 2 632 000 (two million, 6 hundred and thirty-two thousand): 2 millions, 6 hundred-thousands, 3 ten-thousands, 2 thousands, 0 hundreds, 0 tens and 0 units
Note: Small spaces, or commas inserted between groups of three digits, working from right to left, aid the reading of larger numbers.
Rounding whole numbers
Rounding whole numbers involves simplifying them to the nearest defined place value, for example to the nearest Ten, Hundred, or Thousand.
This is useful for estimating, giving an approximate number, which can be easier to picture and quicker to work with.
For example, rounding 227 to the nearest 10, would make it 230. As 7 is closer to 10, it has been rounded up. If, however, the unit was less than 5, it would be rounded down. For example, 223 would become 220.
Rounding and estimating are covered in more detail in the final page of this book.
1.3. Quiz: Numbers and place value
2. Fractions
A fraction is a part, or portion of a whole.
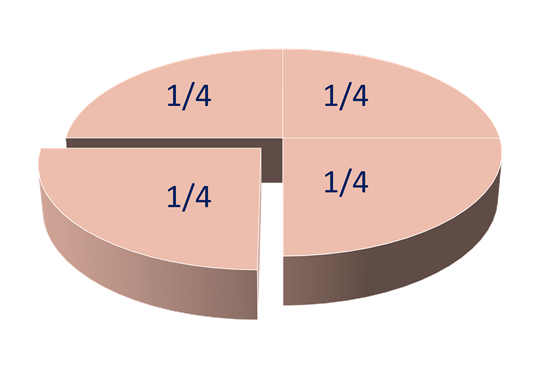
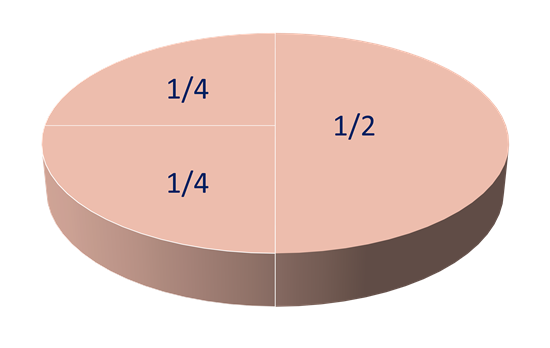
If we divide a cake into four equal portions, for example, each of these is a fourth of the whole. A fourth is also known as a quarter.
A fourth, or quarter, is written as 1 over 4, separated by a line, to represent 1 of 4 equal portions.
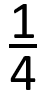
or ¼ when using a keyboard
2.1. Numerator and denominator
We can talk about fractions in terms of numerators and denominators.
The denominator is written below the line, or fraction bar, and is the number of equal parts that something (the whole) has been divided into. Our cake was divided into four equal portions, so the denominator is 4.
The numerator is written above the line, and is the quantity, or number, of those parts that we are interested in. We are looking at the three remaining portions of cake, so the numerator is 3.

2.2. Simplifying fractions
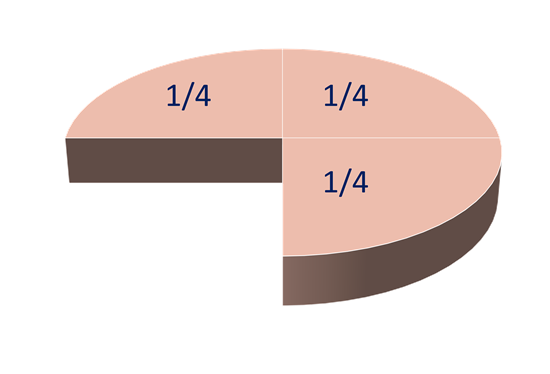
In this simple example, with a cake cut into four equal slices, it is easy to spot that two quarter slices are equal to exactly half of the cake.
Half of anything is written as 1 over 2, to represent one of two equal parts of the whole.
So rather than saying 2/4 (two quarters) of our cake, we can simply say 1/2 (half, or one half).
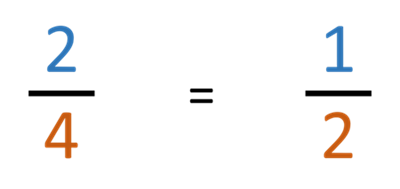
Cancelling down
Mathematically, fractions are simplified using a process known as cancelling down, in which both the numerator and the denominator are divided by the largest number above 1, by which both can equally (i.e. with no remainder) be divided.
Division is the process of breaking a number into equal parts. The division symbol (÷) is used in this operation. For example, when you divide 12 by 4, you break 12 into 4 equal groups of 3 (12 ÷ 4 = 3).
Taking our example of 2/4 equal slices of cake, both the numerator and the denominator can be divided equally by 2.
2 ÷ 2 = 1
4 ÷ 2 = 2
which gives us our simplified fraction of 1/2 (half).
Let’s look at another example.
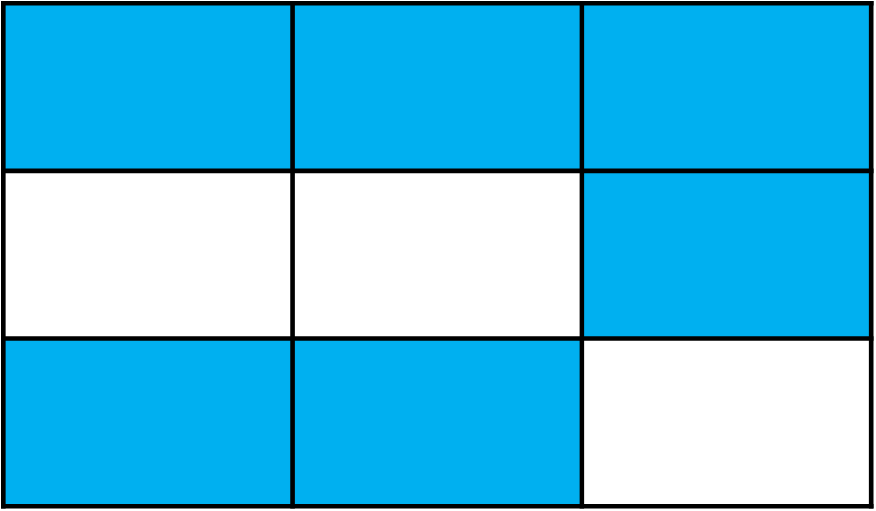
What fraction of this rectangular shape is shaded blue?
We can see that the shape has been divided into 9 equal rectangles, and 6 of these have been shaded. So we can say 6/9 (6 out of nine, 6 ninths) have been shaded.
Can this fraction be simplified?
Remember, we cancel a fraction down by dividing both the numerator and the denominator by the largest number, above 1, by which both can equally be divided.
Well, 6 is the largest number that the numerator (6) can be divided by. Can we divide the denominator (9) by 6? No.
What about 5? No.
4? No.
3? Yes!
Both the numerator and the denominator can be divided equally by 3.
6 ÷ 3 = 2
9 ÷ 3 = 3
which gives us a simplified fraction of 2/3, or two thirds of the whole.
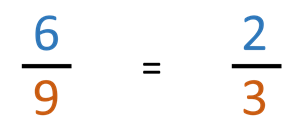
2.3. Quiz: Fractions
3. Decimals
Our numbering system uses ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9), together with place values, to represent whole numbers. For example, 32 apples represents three multiples of ten (3 x 10) apples, and two single apples.
Using a decimal point, we can refer to values ‘in between’ whole numbers, for example, 1.5 is a value between 1 and 2, and 12.25 is a value between 12 and 13.
Digits on the left of a decimal point are whole numbers, while digits on the right represent fractions.
Decimal systems of calculation and measurement are widely used around the world .
These include decimal currency systems, including our own, and the metric system for weights and measures.
Smaller and smaller values can be represented by increasing the number of places used to the right of the decimal point (for example 0.00082), with the first place to the right representing a tenth (1/10), followed by a hundredth (1/100), a thousandth (1/1000) and so on.
3.1. Decimal currency
Like many other countries, we use a decimal currency system. We count in pounds and pennies (pence) and one hundred pence (100p) equals one pound (£1).
Monetary amounts are written with whole pounds (multiples of 100 pence) followed by a decimal point (.) and any remaining pence (adding up to less than 100) after the decimal point.
For example:
- £3.25 (3 pounds and 25 pence)
- £4.99 (4 pounds and 99 pence)
- £8.09 (8 pounds and 9 pence)
Note: Only two places are required after the decimal point, when counting money, as we only need to record values between 00 (zero) and 99 pence.
Try it out
How would you write 7 pounds and 100 pence?
100 pence is equal to 1 pound, so we actually have 8 pounds in total.
This would be written as £8.00 indicating 8 pounds and no pence.
Prior to ‘decimalisation’ in February 1971, the UK’s money system was a bit more complicated!
A pound was worth 4 crowns, or 20 shillings, or 240 pennies. Various other coins represented multiples of a penny, such as the threepenny bit (three pence), sixpence and half a crown.
3.2. Metric measures
The metric system is a decimal based measuring system, in use internationally.
Basic metric units of measurement are summarised below.
Metre
The metre is the basic metric unit for measuring length, for example distance and height.
Smaller measurements, for example when using a ruler or tape measure, include centimetres and millimetres. The ruler below measures up to 15 centimetres, each of which is divided into 10 millimetres.

mbnachhilfe_de atPixabay / Licence
- 1 centimetre = 0.01 metres, one hundredth of a metre.
- 1 millimetre = 0.1 centimetres, one tenth of a centimetre.
Larger measurements, for example distances between places, are taken in multiples of metres, most commonly the kilometre.
- 1 kilometre = 1000 metres.
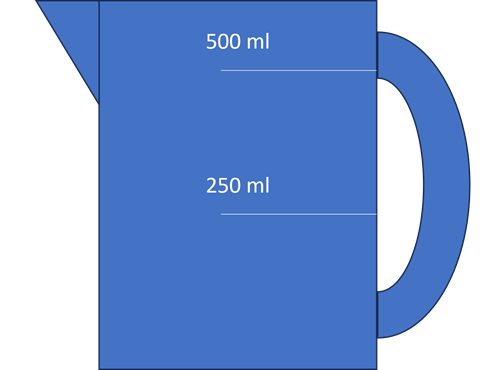
Litre
The litre is the basic metric unit for measuring volume, for example of liquids.
In everday life, liquids are sold, or measured, in multiples of litres (e.g. 2.5 litres) or in millilitres.
- 1 litre = 1000 millilitres.
- 500 millilitres = 0.5 litres, or half a litre.
Gram
The gram is the basic metric unit for measuring weight, for example when you are weighing ingredients for a recipe.
In everyday life, larger quantities, such as your own weight, are measured in kilogrammes.
- 1 kilogram = 1000 grams.
3.3. Converting fractions to decimals
To convert a fraction to a decimal, we divide the numerator (the number above the fraction bar) by the denominator (the number below).
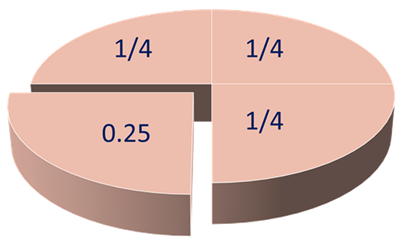
For example, let’s find the decimal value of 1/4 (one fourth, or a quarter).
Using a calculator, divide 1 by 4 (1 ÷ 4):
1 ÷ 4 = 0.25
0.25 is 1/4 expressed as a decimal.
Calculators: Most mobile phones include a 'Calculator' app, as do Windows and Mac OS operating systems on computers and laptops. There are also online calculators you might find useful, for example Calculator.net.
Try it out: 1
If we take one quarter slice away, what is the decimal value of the remaining 3 slices of cake?
There are 3/4 (three quarters) remaining. To express this as a decimal, we divide the numerator (3) by the denominator (4).
3 ÷ 4 = 0.75
so 0.75 is 3/4 expressed as a decimal.
Alternatively, and remembering that fractions are parts of a whole, we could have subbtracted the value that we already knew (1/4 = 0.25), from the whole, to find the remaining value.The whole is 1.00, in decimal terms, so subtracting 0.25 from this tells us that 0.75 remains.
1.00 - 0.25 = 0.75
Try it out: 2

How would you express one and a half (1½) as a decimal?
Convert the fraction (1/2) to a decimal: 1 ÷ 2 = 0.5
Add this to the whole (1): 1 + 0.5 = 1.5
One and a half (1½) is 1.5 as a decimal.
4. Percentages
From the Latin per centum, meaning ‘by a hundred’, a percentage is a value expressed as a fraction of 100, using the percentage symbol (%).
An understanding of percentages is particularly useful for conveying proportions, and making comparisons.
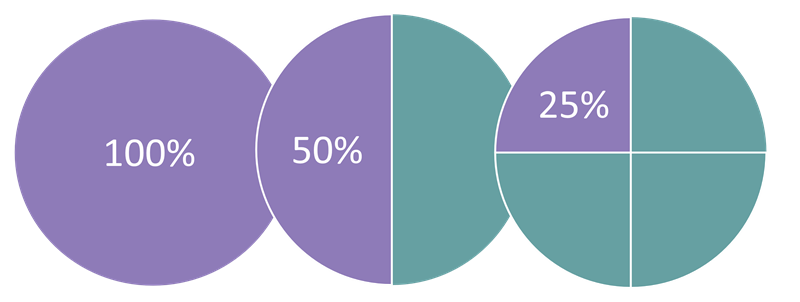
If 100% represents the whole, or total value, of something, whatever that amounts to (the membership of an organisation, for example, or the population of a town), then half of that whole is 50% (100 divided by 2) and a quarter is 25% (100 divided by 4).
Values expressed as percentages are often easier to picture than fractions. Let's look at an example.
Shopping around for a new mobile phone, you find an online store offering to sell your preferred model for only 6/8 (six eighths) of the usual price, while another store is advertising the same phone for 7/10 (seven tenths) of the usual price. Which one appears most attractive?
A further company is offering this model for 75% of the usual price and yet another store is selling for 70% of the usual price. Which of these appears most attractive?
As 70 is less than 75, the 70% price is likely to be the best deal, although you would need to check the usual (100%) price at each company.
Calculate a percentage of a given value
Divide the percentage by 100, and multiply by the given value.
For example:
15% of ticket sales on the first night of an upcoming production by Portimadie Amateur Dramatics Society (PADS) will be donated to the local playgroup.
If ticket sales amount to £800, what will the playgroup receive?
15 ÷ 100 = 0.15
0.15 x 800 = 120
15% of 800 is 120.
Convert a fraction to a percentage
Divide the numerator by the denominator, and multiply by 100.
For example:
90 out of 120 (90/120) members of Portimadie's bowling club participated in a recent competition.
What percentage of the membership was represented?
90 ÷ 120 = 0.75
0.75 x 100 = 75
75% of the membership was represented.
Calculators: Most mobile phones include a 'Calculator' app, as do Windows and Mac OS operating systems on computers and laptops. There are also online calculators you might find useful, for example Calculator.net.
Click the headings below for more examples of percentages in use.
Food packaging must display nutritional information for 100 grammes of that food product. This helps us to make informed choices about what we purchase and consume, particularly when items are sold in different sizes or weights.
You could be looking at two very different foodstuffs, for example a small packet of biscuits and a large bar of chocolate, but if typical values are provided for 100g of that product, you can quickly make a comparison about which product contains the most sugar or fat.
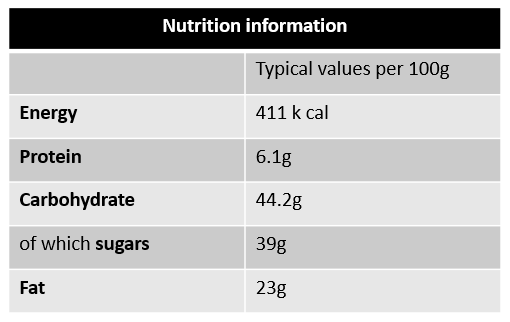

Chocolate cake
by OpenClipart-Vectors at Pixabay
Remembering that a percentage is a value expressed as a fraction of 100, if 39g out of a 100g of a chocolate cake, as shown in the nutrition information label above, is sugar (39/100), then we can also say that 39% of the chocolate cake is sugar.
So, how do we check how much sugar there is in a large, 120g portion of cake?
Method 1
If 39% of the cake is sugar, our 120g portion also contains 39% sugar. To find 39% of a 120g portion, multiply 120 by 39/100 (39 divided by 100).
120 x 39/100 = 120 x 0.39 = 46.8
Which tells us that a 120g portion of this cake contains 46.8g of sugar.
Method 2
Multiply 120 by 39 (120 x 39 = 4680), and then divide that answer by 100 (4680/100 = 46.80).
Dividing whole numbers by 100
To divide a whole number by 100, imagine there is a decimal point to the right of it and then move this decimal point two places to the left.
For example: 457 ÷ 100 = 4.57
If all the digits after a decimal point are zeros, you can ignore them (and the point).
For example: 3200 ÷ 100 = 32
Similarly, to divide a number by 10, move the decimal point one place to the left.
For example: 237 ÷ 10 = 23.7

Try it out
How much sugar is there in a 75g portion of this cake?
There are 29.25g of sugar in a 75g portion of the cake.
75 x 39/100 = 75 x 0.39 = 29.25
A store is offering a 20% discount on everything. If the item you are purchasing normally costs £37.00, how much will you pay?
Original price: £37.00
Discount: 20%
There are several ways you can work out how much you will pay for the item.

Calculate the 20% discount and subtract this from the original price:
- Convert the percentage discount to a decimal: 20% = 20/100 (20 divided by 100) = 0.2
- Multiply the decimal by the original price: 0.2 x 37.00 = 7.4, so a saving of £7.40 (two decimal places are used with money)
- Subtract this from the original price: 37.00 - 7.40 = 29.60
Discounted price: £29.60
Calculate the 80% discounted price:
Knowing that 20% means 20 out of a 100, then subtracting 20 from 100 tells us that we will pay 80% of the original price (100 - 20 = 80).
- Convert 80% to a decimal: 80% = 80/100 (80 divided by 100) = 0.8
- Multiply this by the original price: 0.8 x 37.00 = 29.60
Discounted price: £29.60
Calculate 10% first and work from this:
To find 10% you simply move the decimal point in the original price, one place to the left.
This method, once you have the hang of it, can be quicker to do in your head. Once you have 10%, then to find 20% you simply double it (10 x 2 = 20). Similarly if you were looking at a 5% discount, this would be half of 10% (10 ÷ 2 = 5).
- Calculate 10% of the price: 37.00 divided by 10 (move the decimal point one position to the left) = 3.70
- Multiply by 2 (double it) to find 20%: 3.70 x 2 = 7.40
- Subtract from the original price: 37.00 - 7.40 = 29.60
Alternatively, multiply 10% of the original price by 8 to find 80%.
- Calculate 10% of the price: 37.00 divided by 10 (move the decimal point one position to the left) = 3.70
- Multiply by 8 to find 80%: 3.70 x 8 = 29.60
Discounted price: £29.60
Try it out
If you book early, you can save 30% on the price of a concert ticket.
Original price: £80.00
Discount: 30%
Calculate 10% of the full price and the use this to work out how much you will pay.
10% of £80.00 is £8.00 (80 ÷ 10 = 8).
Applying a 30% discount leaves 70% to pay (100 - 30 = 70).
70% of £80.00 is £56.00 (£8 x 7 = 56).
£56.00 is the discounted price for early purchase.
When managing your household budget, it is important to set money aside for essential expenditure, such as rent or mortgage, utility bills, such as electricity and gas, and food shopping.
Once your essential expenditure is covered, you can then work out what you have left for other expenditure and savings.
The 50-30-20 rule
The 50-30-20 rule is a budgeting method in which a fixed percentage of household income is allocated to three categories of expenditure as follows:
| % of income | Category | Example expenditure |
|---|---|---|
| 50% | Needs | Essential expenses, such as rent or mortgage payments, utility bills, food and transport. |
| 30% | Wants | Non-essentials such as subscriptions, gym membership, entertainment, eating out. |
| 20% | Savings | Putting money into savings or repaying debts such as credit cards or student loans. |
How helpful this method might be will depend on individual circumstances and income, but let’s look at an example of how it could be applied.
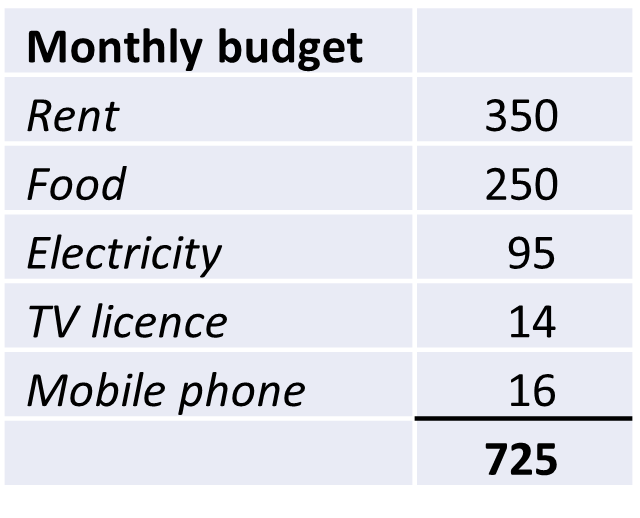
Mairead receives £1700 per month, after tax. She would really like join her friends on a holiday abroad next year but rarely has any money left in her account by the end of the month. One of her friends has suggested she try the 50-30-20 rule to manage her money.
Needs
Mairead notes her essential (Needs) expenditure.
Does the expenditure she has noted under the ‘Needs’ category meet the 50% allowed under the 50-30-20 rule?
| Rent | 350 |
|---|---|
| Travel | 45 |
| Supermarket / weekly shopping | 250 |
| Electricity | 95 |
| Council tax | 80 |
| TV licence | 14 |
| Phone | 16 |
| Total | 850 |
Yes, Mairead’s essential costs do (just) add up to 50% of her income.
50% = ½, so half of Mairead’s income is £1700 ÷ 2 = £850
Wants
Next Mairead looks at her non-essential (Wants) expenditure. Her gym membership and streaming TV services are fixed monthly amounts, but she never keeps an eye on what she spends going out and shopping for clothes.
If she can stick to the rule (30% of income to Wants), this is where she can make some savings.
How much of Mairead’s salary should she allocate to this category?
| Gym | 45 |
|---|---|
| TV streaming subscriptions | 18 |
| Miscellaneous | ? |
Under the rule, Mairead can allocate 30% of her £1700 income to this category.
10% of £1700 is £170. Multiply this by 3 to get 30%, which is £510. Taking into account the fixed expenses, this would leave 447 for all other Wants expenditure.
Savings
The remainder of Mairead’s income can be allocated to the Savings (20%) category.
Mairead currently pays her credit card £120 per month. How much can she allocate to her holiday savings account once she has paid her credit card, under the 50-30-20 rule?
10% of £1700 is £170. Multiply this by 2 to get 20%, which is £340. Subtract the £120 credit card payment which leaves £220 which she can put into a savings account.
If she sticks to her budget, Mairead will have £2640 (220 x 12) in the holiday account in a year's time!

Multiplication and division are covered in more detail in the Operations and calculations book.
4.1. Quiz: Percentages
5. Rounding and estimating
Rounding involves simplifying numbers, to make them easier to work with, for example when estimating. Numbers can be rounded to the nearest ten, hundred or thousand, for example, or to a fixed number of decimal places.
Rounding process
Numbers are rounded up or down to the chosen place value, depending on the digit to its right.
If the digit to the right is
- 5 or above, round up: Increase the digit in the 'rounded' column by 1, and replace the digit(s) to the right with 0.
- Less than 5, round down: Leave the digit in the 'rounded' column as it is, and replace the digit(s) to the right with 0.
Let's look at an example.
Round 2270 to the nearest 100.
| Th | H | T | U |
|---|---|---|---|
| 2 | 2 | 7 | 0 |
The digit to the right of the hundreds column is 7.
This is higher than 5 so we round up.
The digit in the hundreds column (2) becomes 3.
The digits in the columns to the right become 0.
2270 rounded to the nearest 100 is 2300.
Try it out
Round 45037 to the nearest thousand.
| TTh | Th | H | T | U |
|---|---|---|---|---|
| 4 | 5 | 0 | 3 | 7 |
The digit to the right of the thousands column is 0, so we round down.
The digit in the thousands (5) column remains the same.
The digits to the right become 0.
So the answer is 45000.
Rounding to decimal places
When you are working with money, you will always work to two decimal places. For other decimals, with lots of numbers to the right of the decimal point, you may wish to simplify these to a certain number of places.
The process is similar to that described above for whole numbers, however when rounding has taken place, the digits to the right of the decimal place are discarded.
For example, if you are rounding to two decimal places, look at the third digit to the right of the decimal point.
If it is
- 5 or more, increase the second decimal place digit by 1, and discard the digit(s) to the right.
- less than 5, leave the second decimal place digit as it is, and discard the digits to the right.
Let's look at an example.
Round 22.325796 to one decimal place.
| 22.3 | 25796 |
The digit to the right of the first decimal place is 2, which is less than 5 so we round down.
The first decimal place digit (3) remains the same and the digits after this are discarded.
22.325796 becomes 22.3 when rounded to one decimal place.
Try it out
Round 37.5275894 to two decimal places.
| 37.52 | 75894 |
The digit to the right of the second decimal place is 7, which is more than 5 so we round up.
The second decimal place digit (2) is increased by 1, to become 3, and the digits after this are discarded.
37.5275894 becomes 37.53 when rounded to two decimal places.
Rounding and estimating
Rounding is useful for estimating, for example when you are shopping.
As you add items to your basket, it is easier to keep a running tally in your head if you round prices to the nearest pound.
For example,
| Item | Price | Rounded to | Running total |
|---|---|---|---|
| 1 | £0.99 | £1 | £1 |
| 2 | £1.79 | £2 | £3 |
| 3 | £0.43 | £0 | £3 |
| 4 | £0.67 | £1 | £4 |
So the estimated cost of the items in the basket so far is £4.00.
The actual cost is £3.88, so not a bad estimate!
Try it out
Estimate the cost of these items as you add them to your shopping basket by rounding them to the nearest pound and keeping a tally of the rounded prices as you go.
| Item | Price | Rounded to | Running total |
|---|---|---|---|
| 1 | £3.99 | ||
| 2 | £1.76 | ||
| 3 | £1.43 | ||
| 4 | £1.99 | ||
| 5 | £0.67 |

OpenClipart-Vectors at Pixabay
| Item | Price | Rounded to | Running total |
|---|---|---|---|
| 1 | £3.99 | £4 | £4 |
| 2 | £1.76 | £2 | £6 |
| 3 | £1.43 | £1 | £7 |
| 4 | £1.99 | £2 | £9 |
| 5 | £0.67 | £1 | £10 |
How did you get on?
Rounding as you added the items you should have estimated the total cost to be £10. The actual cost of £9.84 is slightly under the estimated cost.

