Operations and calculations
| Site: | OpenLearn Create |
| Course: | Number confidence for work |
| Book: | Operations and calculations |
| Printed by: | Guest user |
| Date: | Sunday, 30 November 2025, 12:51 PM |
1. Introduction
Operation
An operation is a mathematical process, which is carried out on input values, such as numbers, decimals and fractions, to produce an output value, or result. Examples of operations include addition, subtraction, multiplication and division.
The symbols we use to indicate which operation is to be carried out are called operators.
For example:
- + (add)
- – (subtract)
- x (multiply by)
- ÷ or / (divide by)

Image by Vectorportal.com /
CC BY-SA 4.0
Calculation
The process of performing an operation, or series of operations, for a specific purpose, is called a calculation.
For example, you would use addition to total the cost of the items you would like to buy in a store, or subtraction when you realise you do not have enough money to buy them all!
2. Addition
Addition is the process of combining two or more numbers, or quantities, together to find the total value, or sum. The addition, or plus, (+) operator is used to indicate this operation.
Any amount of numbers can be added together in one operation, and in any order.
3 + 2 + 5 = 10 and 5 + 3 + 2 = 10

Long addition | Multiply Highland, 1:42
When we want to add two or more larger numbers together, we can use a method called long addition.
As an example in this video, we will calculate the total of 312, 265, 27 and 10.
To do this we start by listing the numbers we want to add together as a stack, lining them up in columns of units, tens, hundreds and so on.
Starting with the units column on the right hand side, we need to add up all the numbers in that column and write the total value in the answer space at the bottom. In this example our total is 14 which is greater than 9, so we write the units part, four, into the answer space and then write the one for the tens part underneath the answer space for the tens column to the left.
We now move on to add up the numbers in the tens column, including any that were written underneath the answer space, so that includes the one we added in this example. Again, write the total in the answer space separating out the tens and units if necessary. Here the total is 11, so we put a one in the answer space and another one beneath the answer space for the hundreds column.
We repeat this process until we have added up every column. So in this example we have a total of 614.
Long addition worked example
Some numbers, or combinations of numbers are fairly easy to add up in our head, or on our fingers, but for larger numbers, or longer lists of numbers, it is usually easier to write them out first, taking care to keep them in columns according to their place value.
When adding up in columns, we work from right to left.
In the following steps we'll find the sum of 312, 265, 27 and 10.
Write out the numbers to be added, one above the other, with individual digits in columns according to place value - units, tens and hundreds etc. (headings are included here as a reminder).

Add the digits in the units column.
2 + 5 + 7 + 0 = 14
Add the four units below the line in the units column and carry the ten over to the tens column – mark it below the space for the tens total - we'll need to include it in the next step.

Add the digits in the tens column, including the number carried over.
1 + 6 + 2 + 1 + 1 = 11
Add 1 below the line in the tens column and carry 1 over to the next (Hundreds) column.

Add the numbers in the hundreds column, including the number carried over.
3 + 2 + 1 = 6
Add 6 below the line in the hundreds column.
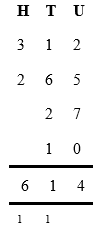
Following this process shows us that the sum of 312, 265, 27 and 10 is 614.
2.1. Adding decimals
When working with decimal values, it is important to ensure that the decimal point is always in the same position (column) in each row of the calculation. This is easier if the same number of decimal places (i.e. positions to the right of the decimal point) are used for each value in the calculation.

Money
When working with money, we use two decimal places to hold values up to 99 pence, so, if we are working with mixed values of pounds and pence, we can include a decimal point and two decimal places for each. Two zeros after the decimal indicate ‘no pence’ and a zero before the decimal point indicates ‘no pounds’.
For example to sum the following amounts:
- Two pounds (£2)
- 99 pence (99p)
- Thirteen pounds (£13)
- Six pounds and five pence (£6.05)
Set them out, one above the other, with the decimal point always in the same position.
Then, working from right to left, add the digits in each column, carrying over as required, as outlined in ‘long addition’ on the previous page.
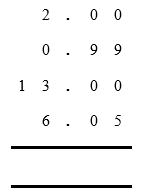
Starting on the far right: 0 + 9 + 0 + 5 = 14. Write 4 below this column and carry the ten over to the column on the left, by marking 1 below the bottom line.
Moving left: 0 + 9 + 0 + 0 = 9, plus the 1 carried over, is 10. Write 0 in this column and carry the ten over to the next column on the left, by marking 1 below.
Moving to the column on the left of the decimal point: 2 + 0 + 3 + 6 = 11, plus the 1 carried over, is 12. Write 2 in this column and carry the ten over, by marking 1 below.
Next column on the left: there's only one digit, so add this to the 1 carried over. 1 + 2 = 2, so write 2 below the line.
Keeping the decimal point in the same position, £22.04 is our total.
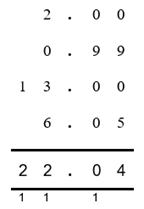
Mixed decimals
It is easier to ensure an accurate result if you use the same number of decimal places (positions to the right of the decimal point) for each value in the calculation, inserting zeros in any which are not required.
For example to sum the following amounts:
- 22
- 17.5
- 33.333
- 0.1257
- 15
Set them out, one above the other, with the decimal point always in the same position:
Then, working from right to left, add the digits in each column, carrying over as required, as outlined in ‘long addition’ on the previous page.

Ignoring the 0s (as they are of no value) add the digits in each columns:
Far right column: 7
Moving left: 3 + 5 = 8
Next left: 3 + 2 = 5
Left again: 5 + 3 + 1 = 9
Left again: add the decimal point
Column to the left of the decimal point: 2 + 7 + 3 + 5 = 17. Write 7 in this column and carry over the 10 by writing 1 below.
Final column: 2 + 1 + 3 + 1 = 7, plus the 1 carried over = 8

2.2. Adding Fractions
There are three steps to follow when adding fractions:
- Ensure the fractions have a common denominator (the numbers below the fraction bars must be the same).
- Add the numerators (the numbers above the fraction bars), placing the total over the denominator.
- Simplify the resulting fraction if possible.

If the fractions do not have a common denominator, they must first be adjusted, using multiplication or division, to use the least common denominator (the smallest multiple they have in common).
Note: To maintain the value of a fraction, you must use the same operation to adjust both the numerator (top number) and the denominator (bottom number).
Multiplication and division processes are covered in separate sections of this book.
Let’s work through some examples.
1/8 + 2/8 (one eighth plus two eighths)
- The denominators are the same (8), so we can go ahead and add the numerators.
- 1 + 2 = 3, which placed over the denominator gives 3/8.
- This cannot be simplified, so the answer is 3/8.
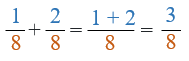
2/3 + 1/6 (two thirds plus one sixth)
-
The denominators are not the same, so we need to find and use the least common denominator.
If we multiply the denominator (3) on the first fraction by 2, this will make it 6, which is the same as the denominator on the second fraction.
We'll go ahead and do that, remembering we also have to multiply the numerator by the same amount.
2 x 2 = 4
3 x 2 = 6
This gives us an adjusted fraction of 4/6.
- 4/6 + 1/6 = 5/6
- This cannot be simplified so the answer is 5/6.
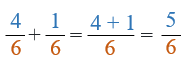
2/6 + 4/7 (two sixths plus four sevenths): Method 1
-
The denominators are not the same, so we need to find the least common denominator, i.e. the smallest multiple they all have in common.
In this method, we multiply the denominators to find the common denominator:
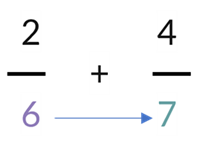
6 x 7 = 42
Then we multiply the numerator of each fraction by the original denominator of the other.
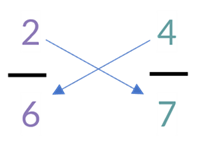
2 x 7 = 14
4 x 6 = 24
Placing these over the common denominator gives us adjusted fractions of 14/42 and 24/42.
- 14/42 + 24/42 = 38/42
- This fraction can simplified to 19/21 by dividing both the numerator (38) and the denominator (42) by 2.
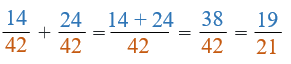
2/6 + 4/7 (two sixths plus four sevenths): Method 2
-
The denominators are not the same, so we need to find the least common denominator, i.e. the smallest multiple they all have in common.
In this method, we list the multiples of each of the denominators until we find the first one they have in common.
The denominators are 6 and 7.
Multiples of 6: 1 x 6 = 6, 2 x 6 = 12, 3 x 6 = 18, 4 x 6 = 24, 5 x 6 = 30, 6 x 6 = 36, 7 x 6 = 42
Multiples of 7: 1 x 7 = 7, 2 x 7 = 14, 3 x 7 = 21, 4 x 7 = 28, 5 x 7 = 35, 6 x 7 = 42
The least common denominator is 42.
Multiply the numerator and denominator of the first fraction (2/6) by 7:
2 x 7 = 14
6 x 7 = 42
This produces the adjusted fraction 14/42.
Multiply the numerator and denominator of the second fraction (4/7) by 6:
4 x 6 = 24
7 x 6 = 42
This produces the adjusted fraction 24/42.
- 14/42 + 24/42 = 38/42
- This fraction can simplified to 19/21 by dividing both the numerator (38) and the denominator (42) by 2.
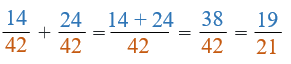
3. Subtraction
Subtraction is the process of taking away a number, or quantity, from another to find the remaining value. The subtraction, or minus, (-) operator is used to indicate this operation.
10 – 6 = 4 (10, take away 6, leaves 4)

Subtracting a larger number from a smaller number
Subtracting a larger number from a smaller number, will result in a negative number.
To work out the answer, switch the numbers so that you can subtract the smaller number from the larger number, and then negate the answer, by prefixing it with a minus (-) symbol.
For example, to find 8 – 12,
- Switch the order of the numbers: 12 - 8
- Carry out the calculation: 12 - 8 = 4
- Negate the answer: -4
3.1. Long subtraction
Also known as the column method, long subtraction involves setting out larger numbers one above the other, then performing the subtraction operation on each column, working from right to left.
Long subtraction | Multiply Highland, 1:56
When we want to subtract one large number from another we can use a method called long subtraction.
To do this we first need to write the numbers out in a stack, with the number that is being subtracted sitting at the bottom. The place values need to be lined up in columns for units, tens, hundreds and so on.
We start with the units column on the right hand side. If the number on the bottom is smaller than the one on the top it should be subtracted. So here we can take away the six from the nine and write the answer three between the horizontal lines at the bottom.
Now we can move to the tens column to the left of the units column. We want to do the same as we did with the units column, but this time the top number is less than the one on the bottom. So here we will need to borrow from the hundreds column.
We do that by crossing out the five in the hundreds column and writing the remaining four next to it. Then we carry over the one that we've borrowed and write it next to the one in the tens column to become 11. Now we can subtract three from eleven and write the answer eight in the answer space for this column.
And finally in the hundreds column, we can subtract the two at the bottom from the four we have pencilled in at the top to give us two in the hundreds answer space. So now we have our answer 283.
Worked example
In the following steps we'll subtract 236 from 519.
Write out the numbers, with the number to be subtracted below the number it is to be subtracted from, keeping individual digits in columns according to place value (headings are included here as a reminder).
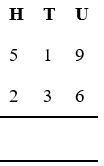
Starting in the units column, subtract the lower digit from the upper digit.
9 – 6 = 3
Write 3 below the line in the units column.
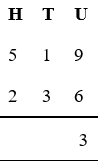
Moving to the tens column, you will notice that the number on the top (1) is smaller than the number to be subtracted (3). When this is the case, we take 10 from the next column on the left.
Remember: as you move from right to left, the numbers in each column are worth ten times (x 10) those in the preceding column.
So, we take 1 away from 5, to leave 4 (noting we have done so by crossing through the 5 and writing in 4). Then we add it (it’s worth 10 in this column) to the 1 to make 11.
Now that we have a larger number on top, we can subtract the number below.
11 – 3 = 8
Write 8 below the line in the tens column.
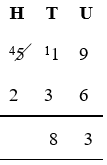
Moving to the next column on the left, subtract the lower digit from the upper digit (which is now 4).
4 – 2 = 2
Write 2 below the line in this column.
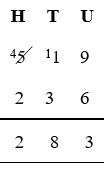
Following this process we find that 519 - 236 = 283.
Tip: We can check our answer is correct by adding the answer to the number subtracted, which should give the number we started with.
i.e. 283 + 236 = 519
In the next page we will look at an example where the number to be subtracted from contains zeros.
3.2. Long subtraction from value containing zeros
Long subtraction with zeros | Multiply Highland, 2:04
When we want to subtract one large number from another we can use a method called long subtraction, but the process can seem a little more challenging if the larger number contains zeros, for example 500 - 236.
To calculate the answer we first need to write the numbers out in a stack with the number that is being subtracted sitting at the bottom. The place values need to be lined up in columns for units, tens, hundreds and so on.
We start with the units column on the right hand side. The bottom number, six, is larger than the top number, 0, so we need to take one from the tens column. However the tens column also has a 0, so we need to take one from the hundreds column.
We therefore cross out the 5 in the hundreds column and write the remaining 4 next to it. We then turn the tens column 0 into 10. Next we take one from this 10, crossing it out to make it 9, and turning the units column 0 into 10.
Now we can subtract 6 from 10 in the units column and write the answer 4 between the horizontal lines at the bottom.
Next we move to the tens column. We now have 9 in the tens column and we need to subtract 3 from the 9. We do this and write 6 in the answer space for this column.
Finally, in the hundreds column, we subtract 2 from the 4 that remains, which gives us 2 in the hundred's answer space. So we now have our answer 264.
Worked example
If the number above is lower than the number to be subtracted, we take 1 from the number immediately to its left (reducing that number by 1) but what if the number to its left is a 0 (zero)?
This is slightly more complicated. Let’s work through an example.
500 – 236
Starting on the right, at the units (U) column, the upper number is 0 (zero). We can't subtract 6 from 0, so we will need to add ten, which we will 'take' from the tens (T) column on the left.
Looking at the tens (T) column however, the upper number is also 0, so we will need to add ten here first, by taking from the column to its left.
Moving to the hundreds (H) column, the upper number is 5, so we can take 1 from this, noting we have done so by crossing through the 5 and replacing it with a 4.
Remember: as you move from right to left, the numbers in each column are worth ten times (x 10) those in the preceding column.
Moving back to the tens column, we can now add 10 to the 0 to make 10, however we then need to take 1 from this to add to the units column, which we do by crossing through 10 and replacing it with 9.
Moving back to the units column, we add 10 to the 0 to make 10. Now we can take 6 from 10 which leaves 4, which we write below the line in this column.
Moving on to the tens column, we take 3 from 9 which leaves 6, which we write below the line in this column.
Finally, in the hundreds column, we take 2 from 4 which leaves 2, which we write below the line in this column.
Following this process, we can see that:
500 – 236 = 264
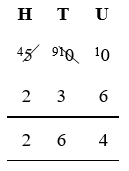
3.3. Long subtraction with a negative result
It is important to note that the long subtraction, or column, method does not work when a smaller value is placed above a larger value.
If it is clear that a subtraction will provide a negative value (i.e. less than 0), swap the order of the numbers, placing the larger number above the smaller number, before carrying out the operation.
This will provide the negative answer required.
Let's look at an example.
Long subtraction with a negative result | Multiply Highland, 2:39
When we want to subtract one large number from another we can use a method called long subtraction, but what if we want to subtract a larger number from a smaller one?
In this video we will calculate 365 minus 420, recognising that 420 is larger than 365 so the result will be negative.
To simplify the process, we can switch the numbers around and subtract the smaller number from the larger one. At the end, we will mark the answer as negative.
Next we write the numbers out in a stack with the larger number, 420, on top and the smaller number, 365, on the bottom. The place values need to be lined up in columns for units, tens, hundreds and so on.
We start with the units column on the right hand side. The bottom number, 5, is larger than the top number, 0, so we need to take one from the tens column.
We cross out the 2 in the tens column and write the remaining 1 next to it. Then we carry over the 1 that we've taken and write it next to the 0 in the units column to become 10. Now we can subtract 5 from 10 and write the answer, 5, between the horizontal lines at the bottom.
Next we move on to the tens column. We need to subtract 6 from the 1 that remains. Since 1 is less than 6 we need to take from the hundreds column.
We cross out the 4 in the hundreds column and write the remaining 3 next to it. Then we carry over the 1 that we've taken and write it next to the 1 in the tens column to become 11. Now we can subtract 6 from 11 and write 5 in the answer space for this column.
Finally, in the hundreds column, we subtract 3 from the 3 that remains which gives us 0 in the hundreds answer space.
So we now have our answer of 55, but remember since we've reversed the numbers to recognize that 420 is larger than 365, our final result is negative therefore the final answer is - 55.
Worked example
365 – 420
As 420 is larger than 365, this operation will result in a value less than 0, so we will swap the numbers before carrying out the operation.
Place the larger number (420) over the smaller number (365) and use the column (long subtraction) method to subtract 365 from 420.
- Units (U) column
- Tens (T) column
- Hundreds (H) column
0 is less than 5, so we take 1 from the column to the left, (crossing out 2, and making this 1) and add it to the 0 to make 10.
Now we can take the number below (5) from this: 10 – 5 = 5
Write 5 below the line, in the same column.
1 is less than 6, so we take 1 from the column to the left (crossing out 4, and making this 3) and add it to the 1 to make 11.
Now we can take the number below (6) from this: 11 – 6 = 5
Write 5 below the line in the same column.
3 – 3 = 0 but as this is the furthest left column, you don't need to write this below the line.
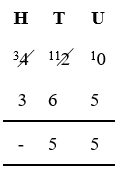
So the answer to 365 - 420 is -55 (minus 55).
3.4. Subtracting decimals
When working with decimal values, it is important to ensure that the decimal point remains in the same position (column) throughout the calculation. This is easier if the same number of decimal places (i.e. positions to the right of the decimal point) are used for each value in the calculation.
Money
When working with money, in mixed values of pounds and pence, include a decimal point and two decimal places in each line of the calculation.
Two zeros after the decimal indicate ‘no pence’ and a zero before the decimal point indicates ‘no pounds’.
For example, to subtract £6.05 (six pounds and five pence) from £13 (thirteen pounds):
- Include a decimal point and two zeros, in the first line of the calculation (£13.00) to indicate thirteen pounds and no pence.
- Write the value to be subtracted (£6.05) in the line below, ensuring the decimal point is in the same position as in the line above.
- Ensuring the decimal point remains in the same position, subtract the lower value from the one above, using the long subtraction (column) process.
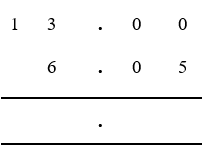
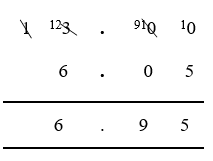
- Starting in the far right (2nd decimal place) column, 0 is less than 5, so we need to take 1 over from the column on the left.
- The next left (1st decimal place) column also contains 0, however, so we need to take 1 from the next left (units) column, to the left of the decimal point.
- In the units column take 1 from 3 (cross through 3 and mark as 2).
- Carrying right (1st decimal place) 10 + 0 = 10, but we need to take 1 from this to carry right again (cross through 10 and mark as 9).
- Carrying right (2nd decimal place), 10 + 0 = 10, and 10 – 5 = 5
- Moving left (1st decimal place), 9 – 0 = 9
- Left again (units column), 2 is less than 6, so we need to take 1 over from the (tens) column to the left (cross through 1, and mark as 0).
- Carrying right, 10 + 2 = 12, and 12 – 6 = 6
Remember that 1 in any position is worth 10 when added to the column immediately to its right.
The tens column now only contains 0, so this is the end of the process.
Mixed decimals
It is easier to ensure an accurate result if you use the same number of decimal places (positions to the right of the decimal point) for both values in the calculation, inserting zeros in any which are not required.
For example to subtract 17.5 from 24.247:
- Write 24.247 on the first line
- Write 17.500 (which includes two additional zeros to match the decimal places in the value above).
- Ensuring the decimal point remains in the same position, subtract the lower value from the one above, using the long subtraction (column) process.
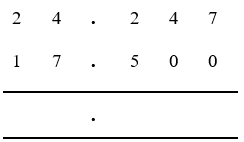
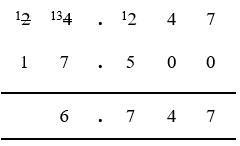
- Far right (3rd decimal place) column, 7 - 0 = 7
- Moving left (2nd decimal place), 4 - 0 = 4
- Moving left (1st decimal place), 2 is less than 5, so take 1 from the next (units) column to the left (cross through 4 and mark as 3).
- Carrying right, 10 + 2 = 12, and 12 - 5 = 7
- Left again (units column), 3 is less than 7, so take 1 from the (tens) column to the left (cross through 2 and mark as 1).
- Carrying right, 10 + 3 = 13, and 13 - 7 = 6
- Left again (tens column), 1 - 1 = 0, and as whole numbers can't start with 0, leave this column blank.
3.5. Subtracting fractions
There are three steps to follow when subtracting fractions:
- Ensure the fractions have a common denominator (the numbers below the fraction bars must be the same).
- Subtract the numerators (the numbers above the fraction bars), placing the total over the denominator.
- Simplify the resulting fraction if possible.
If the fractions do not have a common denominator, they must first be adjusted, using multiplication or division, to use the least common denominator (the smallest multiple they have in common).
Note: To maintain the value of a fraction, you must use the same operation to adjust both the numerator (top number) and the denominator (bottom number).
Multiplication and division processes are covered in separate sections of this book.
Let’s work through some examples.
3/8 - 1/8 (three eighths minus one eighth)
- The denominators are the same (8), so we can go ahead and subtract the numerators.
- 3 - 1 = 2, which placed over the denominator gives 2/8.
- This can be simplified by dividing both the numerator and the denominator by 2, giving the answer 1/4.
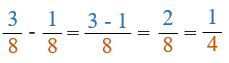
1/3 - 1/6 (one third minus one sixth)
-
The denominators are not the same, so we need to use the least common denominator (the smallest multiple they have in common).
If we multiply the denominator (3) on the first fraction by 2, this will make it 6, which is the same as the denominator on the second fraction.
We'll go ahead and do that, remembering we also have to multiply the numerator by the same amount.
1 x 2 = 2
3 x 2 = 6
This gives us an adjusted fraction of 2/6
- 2/6 - 1/6 = 1/6
- This fraction cannot be simplified so the answer is 1/6.
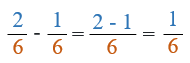
3/4 - 2/5 (three quarters minus two fifths): Method 1
-
The denominators are not the same, so we need to use the least common denominator:
In this method, we multiply the denominators to find the common denominator:
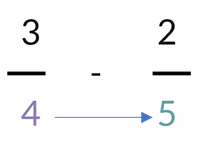
4 x 5 = 20
Then we multiply the numerator of each fraction by the original denominator of the other.
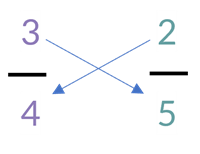
3 x 5 = 15
2 x 4 = 8
Placing these over the common denominator gives us adjusted fractions of 15/20 and 8/20.
- 15/20 - 8/20 = 7/20
- This fraction cannot be simplified, so the answer is 7/20.
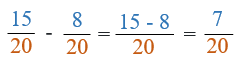
3/4 - 2/5 (three quarters minus two fifths): Method 2
-
The denominators are not the same, so we need to use the least common denominator:
In this method, we list the multiples of each of the denominators until we find the first one they have in common.
The denominators are 4 and 5.
Multiples of 4: 1 x 4 = 4, 2 x 4 = 8, 3 x 4 = 12, 4 x 4 = 16, 5 x 4 = 20
Multiples of 5: 1 x 5 = 5, 2 x 5 = 10, 3 x 5 = 15, 4 x 5 = 20
The least common denominator is 20.
Multiply the numerator and denominator of the first fraction (3/4) by 5:
3 x 5 = 15
4 x 5 = 20
This gives us an adjusted fraction of 15/20.
Multiply the numerator and denominator of the second fraction (2/5) by 4:
2 x 4 = 8
5 x 4 = 20
This gives us an adjusted fraction of 8/20.
- 15/20 - 8/20 = 7/20
- This fraction cannot be simplified, so the answer is 7/20.
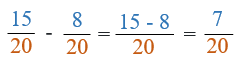
3.6. Everyday activity
Calculating electricity or gas usage
Subtraction is an operation you can use to work out how many units of electricity or gas you have used since the last reading you submitted your last reading.
For example, this meter is currently reading 50682 (the number in the far right, red, box can be ignored).
The previous reading submitted was 50522.
The amount of units used is the difference between the two readings. To find the difference, subtract the previous reading from the current reading.

Try it out
How much electricity has been used since the last meter reading?
160 KWh has been used.
Subtract the previous reading (50522) from the current reading (50682) to find the difference:
50682 - 50522 = 160
4. Multiplication
Multiplication involves adding the same number to itself multiple times, and we use the multiply, or times, (x) operator to indicate this.
So rather than:
2 + 2 + 2 + 2 + 2 + 2 = 12 (6 lots of 2 added together)
we could simply say:
6 x 2 = 12 (six times two, or six twos).
Note that the same result is achieved when swapping the numbers around, i.e.
2 x 6 = 12 (two times 6, or two sixes).

Times tables
You may have learned your ‘times tables’ by rote, when you were at school, chanting them out aloud, over and over until they stuck:
“One two is two, two twos are four, three twos are six….”
Learning and being able to recall the relevant sections, e.g. “six twos are twelve” helps with mental arithmetic (doing quick calculations in your head).
Using a grid
You can also use times tables written as a grid, such as the one shown here, which covers multiples of 1 to 12.
The result of 6 x 2 can be found where the lines from 6 on one axis and 2 on the other intersect, as highlighted.
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
4.1. Tips and tricks
Remember that you can switch the numbers around and get the same result.
So, if you know that 7 x 8 = 56, then you also know that 8 x 7 = 56.
2 x (two times)
If you multiply a number by 2, you are simply adding that number to itself (doubling it).
For example:
2 x 8 = 16 (8 + 8) and 2 x 30 = 60 (30 + 30).
4 x (four times) and 8 x (eight times)
When multiplying a number by 4, you are doubling it twice, and when multiplying by 8, you are doubling it 3 times.
For example,
4 x 7 = 28 (7 doubled is 14, and 14 doubled is 28)
8 x 7 = 56 (7 doubled is 14, 14 doubled is 28, and 28 doubled is 56).
10 x (ten times) and multiples of 10
When you multiply a number by 10, you simply add a 0 to the end of the number.
So,
6 x 10 = 60, and 50 x 10 = 500
You can also multiply by multiples of 10 by initially ignoring the 0s, multiplying the other two numbers, and then appending the 0s back on the end.
5 x 50 = 250 (5 x 5 = 25, append the zero to make 250) and 9 x 70 = 630 (9 x 7 = 63, append the zero to make 630)
6 x 700 = 4200 (6 x 7 = 42, add the zeros to make 4200).
11 x (eleven times)
The first nine are easy – just repeat the number you’re multiplying by.
For example:
2 x 11 = 22, 3 x 11 = 33 up to 9 x 11 = 99
9 x (nine times)
Append a zero to each number to be multiplied by 9 (i.e. multiply by 10) and then subtract the original number.
For example:
4 x 9 (append a zero to the 4 to make 40, and then take away 4) = 36
14 x 9 (append a zero to 14 to make 140, and then take away 14) = 126
30 x 9 (append a zero to make 300, then take away 30) = 270
Quick method for 1 x 9 up to 10 x 9
Hold out ten fingers and then bend the digit (finger or thumb) relating to the number to be multiplied by 9. The number of digits either side indicates the answer.
For example: 4 x 9
Bend down finger 4 and note that there are 3 digits to the left of this and 6 to the right. So 4 x 9 = 36!
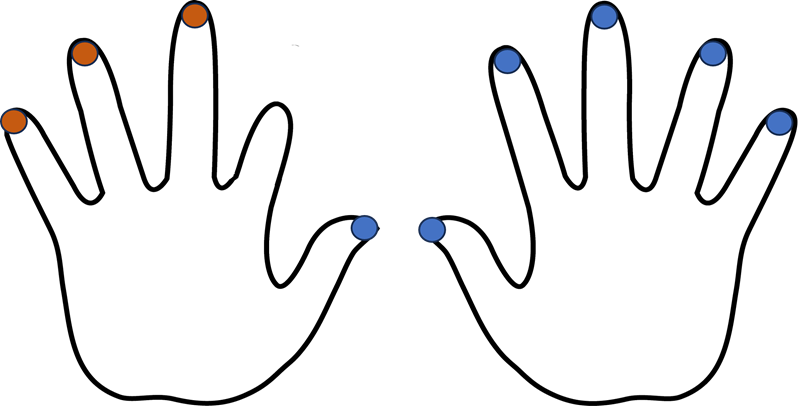
4 x 9 = 36
4.2. Long multiplication
Long multiplication is a written method for multiplying larger numbers, which involves simplifying the operation by breaking it into a series of smaller operations. The results of these are then added together to find the total.
Let's look at an example.
Long multiplication | Multiply Highland, 2:46
When we want to multiply two large numbers, we can use a method called long multiplication.
Let's look at 836 x 14 as an example.
To do this we first need to write the numbers out with one number on top of the other. The smaller number usually goes on the bottom and the digits need to be lined up in columns for units, tens, hundreds and thousands.
We start by multiplying 836 by the tens digit of 14 which is 1. Since it's in the tens place, we actually multiply by 10. 836 x 10 = 8,360 so we write 8,360 down as our first partial product. Next, on a new row, we will multiply 836 by the units digit of 14 which is 4.
We start by multiplying the units digit, which is 6, by 4. The result is 24. We write the 4 in the units place of the second row and carry over the two to the next column.
Next we multiply the 3 in the tens column by 4 to make 12, and add the two we carried over to make 14. We write the 4 in the tens place and carry over the 1 to the next column.
Then we multiply the 8 of the hundreds column by 4. The result is 32, plus the one we carried over, making it 33. So we write 33 in the hundreds and thousands places of this row. Now we have our second partial product 3,344.
The final step is to add the two partial products together. In the units column we have 0 + 4 which is 4. In the tens column we have 6 + 4 which is 10. We write 0 and carry over 1.
In the hundreds column we have 3 + 3, plus 1, which is 7. In the thousands column we have 8 + 3 which is 11. We write 1 and carry over 1. And in the ten-thousands column we have 1 from the carryover so we now have our answer of 11,704.
Worked example
836 x 14
In this method, starting on the right, we multiply each digit in the top row, first by the far left digit in row below, and then by the next digit, and so on.
Each set of answers is noted in a new row, and then all the rows are added together to give the final answer.
To start the process, write the smaller number below the larger number, aligning the digits in columns, according to place value, and draw a line below.
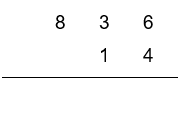
Add 0 below the line, in the units column.
Now we're ready to multiply each digit on the top row by the digit in the tens position (1) in the row below.
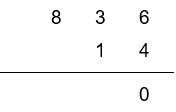
Starting on the right:
6 x 1 = 6, write 6 in the column to the left of the 0.
3 x 1 = 3, write 3 in the next column left.
8 x 1 = 8, write 8 in next column left.
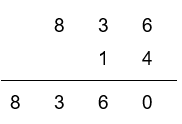
Starting on a new line, working from right to left, we'll now multiply each digit in the top row by the digit in the units position (4) in the row below.
6 x 4 = 24
Write 4 in the units column, and note 2 below the tens column, as a reminder to add it to the result of the next multiplication.

3 x 4 = 12
Plus the 2 carried over:
12 + 2 = 14
Write 4 in this column and note 1 below the next column on the left.

8 x 4 = 32
Plus the 1 carried over:
32 + 1 = 33
Write 3 in this column, and carry 3 (3 tens) to the column on the left. As this was the final multiplication in this row, it can be written straight into the answer line.
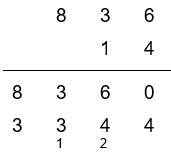
Draw a line below the two rows created during the process so far.
We can now start adding these two rows together.
Starting on the right,
0 + 4 = 4, write 4 below the line.
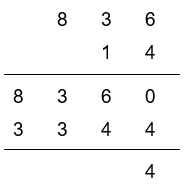
6 + 4 = 10, write 0 below the line and carry 1 (1 ten) to the column on the left, noting it below.
3 + 3 = 6, plus the 1 carried over comes to 7. Write 7 below the line.
8 + 3 = 11, write 1 below the line and 1 in the next column to the left.

836 x 14 = 11704
In this process we multiplied the top number by each of the lower number's place value components (10 and 4):
836 x 10 = 8360 and 836 x 4 = 3344
These solutions were then added together:
8360 + 3344 = 11704
4.3. Everyday activity
Calculating the cost of electricity or gas usage
Multiplication is an operation you can use to work out the cost of the electricity or gas units consumed since the last reading submitted.
For example, this meter is currently reading 50682 (the number in the far right (red) box can be ignored).
The previous reading submitted was 50522.
The amount of units used is 160, which is the difference between the two readings (50682 - 50522 = 160).
Multiply the usage by the charge per kWh to find the cost of the electricity used since the last reading submitted.

Try it out
Multiply the usage (160) by the charge per kWh (currently 13p) to find the cost of the electricity used since the last reading submitted.
£20.80
160 x 13 = 2080
Place a decimal point in front of the last two numbers to separate whole pounds from pence.
5. Division
Division is the process of breaking a number into equal parts. The division symbol (÷) is used in this operation.
For example, when you divide 12 by 4, you break 12 into 4 equal groups of 3:
12 ÷ 4 = 3

The number to be divided.
12
The number to be divided by.
÷ 4
The result of the operation.
= 3
If the dividend cannot be divided exactly into the divisor, the number left over is the remainder.
5.1. Short division
Short division is a written method for dividing large numbers by a single digit number, or a two-digit number which is a familiar divisor, such as 12 (if you know your 12 times table).
Let's look at an example.
832 ÷ 8
The number to be divided (the dividend) is placed in a two-sided box, which looks a bit like a bus stop.
The number it is to be divided by (the divisor) sits just to the left.
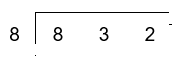
Working from left to right, we divide each digit of the dividend by the divisor, placing the answer above the dividend.
8 ÷ 8 = 1, so we place 1 above the 8.
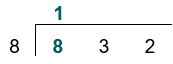
Moving to the right,
3 cannot by divided by 8, so we place a 0 above the 3, and carry 3 (3 x 10) across to the next digit on the right, to make 32.:
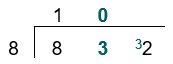
Now we can try dividing 32 by 8.
32 ÷ 8 = 4, so we write 4 above the 2:
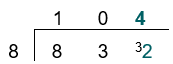
832 ÷ 8 = 104
5.2. Long division
Long division is an expanded version of the short division method. It’s useful when the divisor is a larger number, with two digits or more.
Let’s look at an example.
3888 ÷ 12
We start off in the same way, setting out our digits with the dividend (3888) in a box and the divisor (12) to the left of the box.

Looking at the first digit of the dividend: 3 cannot be divided by 12, so we combine it with the digit on its right, to make 38.
How many times can 38 be divided by 12?
The nearest we can get, without going over, is 3 x 12 = 36, so we write 3 above the line and 36 below 38, ready to subtract it.
38 – 36 = 2
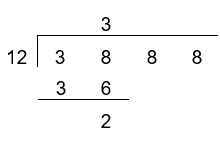
Now we pull down the next digit in the dividend (8), placing it next to the remainder (2) to make 28. How many times can 28 be divided by 12?
The nearest we can get, without going over, is 2 x 12 = 24, so we write 2 above the line and 24 below 28, ready to subtract it.
28 – 24 = 4
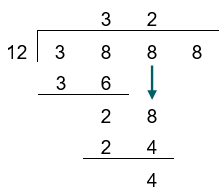
Next, we pull down the final digit in the dividend (8), placing it next to the remainder (4) to make 48.
How many times can 48 be divided by 12?
4 x 12 = 48, with no remainder, so we write 4 above the line and we can write 48 below, just to confirm this.
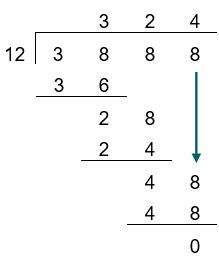
3888 ÷ 12 = 324
Try it out
4037 ÷ 11
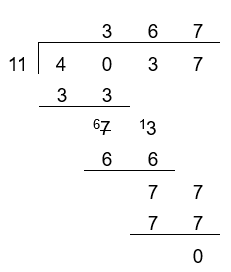
4 cannot be divided by 11, so combine it with the next number to make 40.
3 x 11 = 33
Write 3 above the line and take 33 away from 40, to leave a remainder of 7.
Pull down the next digit (3) to make 73.
6 x 11 = 66
Write 6 above the line and take 66 away from 73, to leave 7.
Pull down the final digit (7) in the dividend, to make 77.
7 x 11 = 77
Write 7 above the line and 77 below 77, to confirm there is no remainder.
4037 ÷ 11 = 367