Shape, space and measures
| Site: | OpenLearn Create |
| Course: | Number confidence for work |
| Book: | Shape, space and measures |
| Printed by: | Guest user |
| Date: | Sunday, 30 November 2025, 12:16 PM |
1. Shape
Shapes are representations, in the form of boundaries (edges or sides) and angles, of objects we might see around us in everyday life.
Shapes can be 2-dimensional (2-D, flat), measured in terms of length and width, or 3-dimensional (3-D, with depth), measured in terms of length, width and height.

Polygons
In this resource we look at polygons: 2-D shapes formed from 3 or more connected straight lines, or edges, with a corresponding number of corners (or vertices).

1.1. Angle
An angle is a measure of a turn, for example between the two lines that form the internal corners of a polygon.
Angles are measured in degrees (°) out of 360. A full turn (as in a circle) is 360°. (Note that a circular shape is not a polygon as it is made up of curves rather than straight lines).
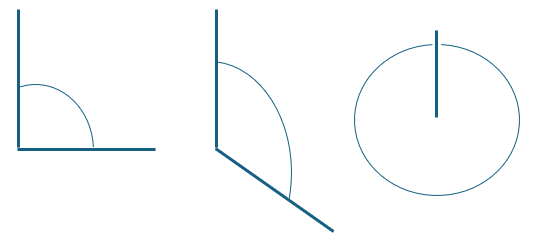
Number of angles in a polygon
The number of angles within a polygon corresponds to the number of sides, or edges, of the polygon. For example:
- 3 sides (triangle) : 3 angles
- 4 sides (quadrilateral) : 4 angles
Sum of degrees in a polygon
The internal angles of a polygon always add up to the same number of degrees, corresponding to its number of edges.
- 3 angles (triangle): 180°
- 4 angles (quadrilateral): 360°
The sum of degrees in the angles of a regular polygon can be confirmed using the following formula:
180° × (n - 2)
where n is the polygon's number of edges.
For example a pentagon has 5 sides, so n - 2 is 5 - 2 = 3. The internal angles, therefore, add up to 180° × 3 = 540°.
Try it out
What is the sum of angles in a hexagon (6 sided polygon)?

A hexagon has 6 sides, so n - 2 is 6 - 2 = 4. The internal angles, therefore, add up to 180° × 4 = 720°.
1.2. Triangle
Triangles are polygons with three sides and three angles. There are four types of triangle, but the angles always total 180°.
Equilateral
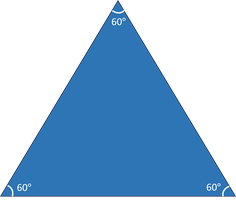
Equilateral triangles have three sides of equal length and three 60° angles.
Isosceles

Isosceles triangles have 2 sides of equal length and 2 equal angles.
Right-angled
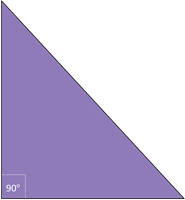
Right angled triangles, as the name suggests, have one 90° (right) angle.
Scalene

All the sides in scalene triangles are different lengths, and none of the angles are equal.
1.3. Quadrilateral
Quadrilaterals are 2-dimensional (flat) polygons with 4 sides, and 4 angles totalling 360° (360 degrees). Here are some examples.
Square

A square has four sides of equal length, and four 90° (right) angles.
Rectangle

A rectangle has four 90° (right) angles, and the sides opposite each other are of equal length.
Parallelogram

The opposite sides of a parallelogram are parallel and equal in length, and opposite angles are equal.
Parallel lines run the same distance apart for their entire length, as in the opposite sides of a square, rectangle or parallelogram.
Perpendicular lines join at right angles (90°) as in the those forming the corners of a square or rectangle.
Trapezium

A trapezium has two sides which run parallel to each other, and two which do not, and two sets of equal angles.
1.4. Regular and irregular polygons
All sides in a regular polygon are of equal length, and the internal angles are equal too, whereas those of an irregular polygon are of varying sizes.
Regular pentagon

A regular pentagon has 5 equal sides and five equal angles totalling 540°.
Irregular pentagon

An irregular pentagon has 5 sides of varying lengths and 5 differently sized angles totalling 540°.
Regular octagon

An octagon has 8 equal sides and 8 equal angles, totalling 1080°.
2. Space
Area
The area is the measure of space taken up by a 2-dimensional (flat) shape.
On the following pages we will look at how to calculate the area of common 2-dimensional shapes.
2.1. Area of a square or rectangle
To work out the area of a square or rectangular shape, for example to measure a floor space or a wall, measure both sides from one corner, and then multiply one by the other.
These sides can be referred to as width x height, width x length or base x height.
Let’s look at some examples.
Measuring a floor space

This floor area is a rectangle which measures 3 metres by 6 metres. To calculate the floor area, multiply 3 metres by 6 metres.
3 x 6 = 18, so the floor area is 18 m2 (18 square metres).
Measuring wall space
Measure the length and height of each wall, and use these measurements to calculate its area. Then add them together to find the total wall space.

Room measurements:
Height: 2.5 m
Length: 4 m
Width: 3 m
Walls 1 and 3: Length (4) x height (2.5) = 10 m, 2 x 10 = 20
Walls 2 and 4: Length (3) x height (2.5) = 7.5 m, 2 x 7.5 = 15
Total area: 20 + 15 = 35 m2 (35 square metres).
You may also wish to subtract, or estimate, the space taken up by windows and doors, for example if working out how much wallpaper or paint to buy.
Try it out
Calculate the number of slabs required to lay paving in a 3 m x 3 m garden area.
Each slab measures 500 x 500 mm.
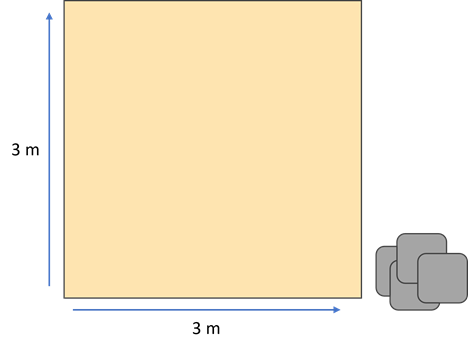
You will need 36 slabs.
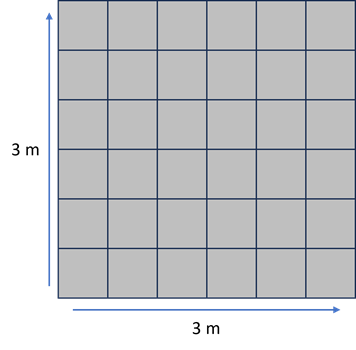
Each slab is 0.5 x 0.5 = 0.25 m2
The area to be covered is 3 x 3 = 9 m2.
Each slab is 0.25 m2, so 4 of these will cover 1 m2 (0.25 x 4 = 1). Multiply 4 x 9 to find the total required.
Alternatively, 9 ÷ 0.25 = 36.
2.2. Area of a parallelogram
If you were to remove the right angled triangle, starting from the base on one side of a parallelogram, you would find that it would fit exactly onto the other side of the parallelogram to form a rectangle.
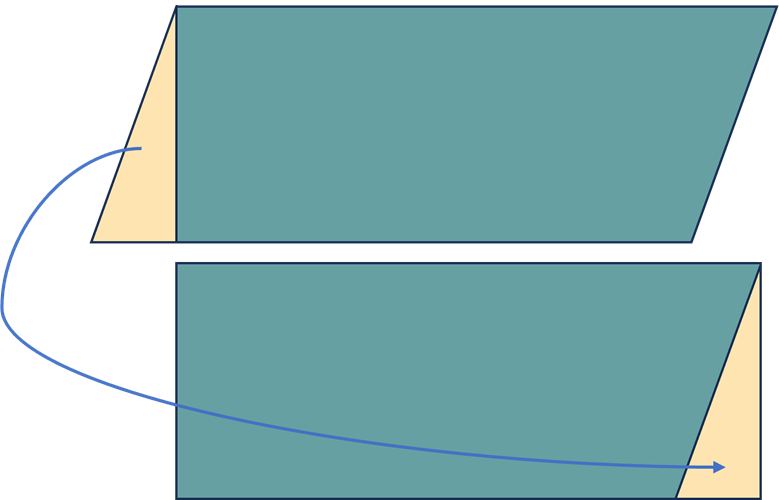
So the area of a parallelogram can be measured by multiplying its length by its perpendicular height, i.e. its height measured at a 90° (right) angle from the base.

This parallelogram measures 5 cm along the base and has a height of 2 cm, so the area is:
10 x 2 = 20 cm2
2.3. Area of a trapezium
A copy of a trapezium, rotated 180°, and joined with the original creates a parallelogram, so a trapezium can be thought of as half a parallelogram.

The area of a trapezium, therefore, can be thought of as the area of the parallelogram, divided by 2.
So area (A) is half of the top (a) + the base (b), multiplied by the height (h), calculated using this formula:
𝑨 = 1/2 (𝒂 + 𝒃)𝒉.
For example, this trapezium is 2.5 cm along the top (a), 5 cm along the base (b) and 3 cm in height (h).
So the area is:
1/2 (2.5 + 5)3
Breaking this down: the part in brackets is always calculated first. The number after the brackets is then multiplied by this.
So the area is:
(𝒂 + 𝒃) = 2.5 + 5 = 7.5
multiplied by 𝒉 = 7.5 x 3 = 22.5
22.5 ÷ 2 = 11.25 cm2
Try it out

What is the area of this trapezium, which measures 3 cm along the top (a) 4 cm along the base (b) and 2 cm in height (h)?
The formula is:
𝑨 = 1/2 (𝒂 + 𝒃)𝒉.
So the area is:
1/2 (3 + 4)2
3 + 4 = 7
7 x 2 = 14
14 ÷ 2 = 7 cm2
2.4. Area of a triangle
The area of a triangle is always half that of a rectangle with the same height and width.
To find the area of a triangle, therefore, we multiply the width (or base) by the height, and then divide that by 2.
For example, in this right-angled triangle, the base measures 10 and the height measures 11.
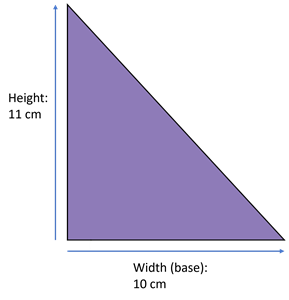
So the area is:
10 x 11 = 110
110 ÷ 2 = 55 cm2
Try it out
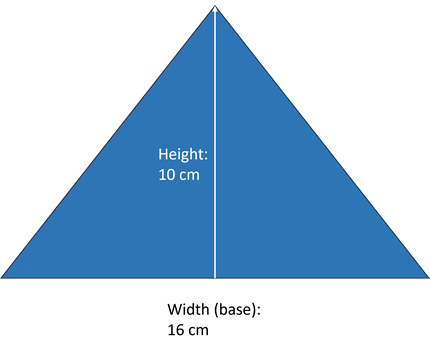
What is the area of this triangle, which measures 16 cm along the base and 10 cm in height?
The area is:
16 x 10 = 160
160 ÷ 2 = 80 cm2
3. Measures
The Metric system of measurement was adopted in the UK in 1967, and in 2000 it became a legal requirement that traders should use this system to sell produce.
The basic Metric measures for length, weight and volume are outlined below.
Length
Length, and distance, are measured in millimetres (mm), centimetres (cm), metres (m) and kilometres (km).
10 mm = 1 cm
100 cm = 1 m
1000 m = 1 km

Weight
Weight is measured in grams (mm) and kilograms (kg).
1000 g = 1 kg
Volume
Volume is measured in millilitres (ml) and litres (l).
1000 ml = 1 l

3.1. Converting measures
Prior to the Metric system of measurement being formally adopted, the Imperial system was used in the UK and is still in use in every day life. Many people still think in 'pounds and ounces', for example when following a recipe. Distances in the UK are also given in 'miles', and speeds in 'miles per hour'.
Unlike the decimal based Metric system, Imperial measures are made up of varying quantities of smaller measures. For example, there are 12 ounces in a pound (1 lb), and 14 lb in a stone.
Some conversions between Imperial and Metric measures are easier to estimate than others, for example 1 mile is approximately 1.6 kilometres, and 1 inch is approximately 2.5 centimetres.
Approximate (rounded down) conversion rates for common length, weight and volume measures are summarised below.
Length
The imperial system of measuring length includes inches, feet and miles.
1 cm = 0.3937 inches (in)
1 m = 3.2808 feet (ft)
1 km = 0.6214 miles (mi)
1 inch (in) = 2.54 cm
1 foot (ft) = 30.48 cm, 0.3048 m
1 mile = 1.6093 km
Weight
The imperial system of measuring weight, or mass, includes ounces, pounds and stones.
1 g = 0.0353 ounces (oz)
1 kg = 2.2046 pounds (lb)
1 ounce (oz) = 28.3495 g
1 pound (lb) = 0.4536 kg
1 stone = 6.3503 kg
Volume
The Imperial system of measuring volume includes pints and gallons.
1 litre = 1.7597 pints
1 pint = 0.5683 litres
1 gallon = 4.5461 litres
Try it out
What is 12.5 stone to the nearest kilogram?
79 kilograms.
12.5 x 6.3503 = 79.37875, which rounds down (as digit after the decimal point is less than 5) to 79.