Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Sunday, 9 November 2025, 6:41 PM
Module 3: Investigating measurement and data handling
Section 1: Introducing measurement
Key Focus Question: How can you explore pupils’ prior knowledge of measure, and plan practical activities to develop understanding?
Keywords: planning; measurement; heartbeat; mind map; prior knowledge; resources
Learning Outcomes
By the end of this section, you will have:
- used mind maps to find out what pupils already know about measurement and measuring;
- used cross-curricular teaching to see how subject areas are interlinked;
- planned your lessons to meet pupils’ needs in developing their understanding of measure.
Introduction
We measure lots of things in our daily lives, such as our height, the weight of our vegetables, how far we have walked.
What examples of measurement would you expect your pupils to be familiar with? Without class-sets of measuring instruments, how can your pupils work with real quantitative data, so that they understand where the numbers come from and what they mean? And how do you help them make sense of prefixes like ‘mega-‘ and ‘milli-‘? This section will help you explore all of these issues.
1. Using mindmaps
Using a mind map will help you find out what your pupils already know about measurement in everyday life. This information will help you plan activities that will extend their understanding further. See Key Resource: Using mind maps and brainstorming to explore ideas for ways to do this.
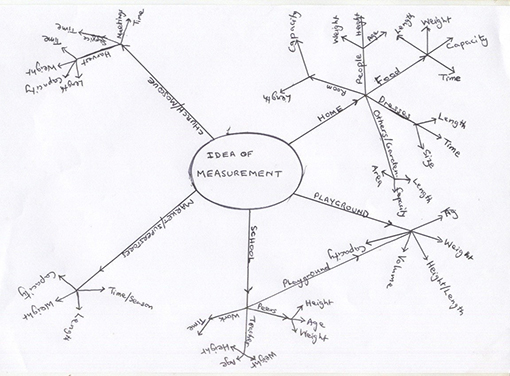
Resource 1: A measurement mind map shows a sample mind map of one group’s ideas.
Case Study 1: Find out what your pupils know
Mrs Lekan in Nigeria wanted to find out what her pupils already knew about measurement in everyday life. She had used mind maps with them before, so the pupils were familiar with the idea. (See Key Resource: Using mind maps and brainstorming to explore ideas.)
Dividing pupils into groups of five, she assigned the groups a focus for their mind maps: to some, she said ‘time’; to others, ‘distance’, to others, ‘weight’.
She asked each group to complete a mind map showing all that they could think of in relation to their particular focus; she reminded them to think of all the different places they might come across measurement – at home, in school, at the market.
After they had worked on this for about 15 minutes, she asked each group with the same focus topic to display their mind maps together.
She gave the whole class ten minutes to look at the mind maps and then discussed the similarities and differences. She listed the similarities and used these as a basis for planning more work on each area.
Activity 1: Using a mind map for measurement
- If you have not used mind maps before, read Key Resource: Using mind maps and brainstorming to explore ideas. Try drawing your own mind map of a subject you have recently taught, to become familiar with the process.
- Begin your lesson by discussing mind maps and how they work. Next, ask groups to work for 15 minutes on their own mind maps on measurement. Bring them together and display their mind maps (see Resource 1 for an example) or for the first time you could do a class mind map where you write down the ideas your pupils suggest.
- Discuss with the whole class the similarities and differences between the mind maps. What are the common ideas?
- Ask pupils to explain any ideas that are not clear and ask them to think of questions they have about measurement. List these and areas they have identified e.g. time, distance. These will help you in planning the next steps.
After the lesson, write down all the ways you think mind maps can help your teaching and your pupils’ learning. See Resource 2: How mind maps can help mathematics teachers and pupils for ideas. Since they are listed there, what practical use is served by writing them down yourself?
2. Measuring heartbeats
Consider asking a science teacher to help you show your pupils how to measure their heartbeats or have a go yourself using Resource 3: Heart rate to help you. This is an excellent introduction to actual measurement, as it can be done without any instruments other than one watch with a second hand for the teacher or pupil to use. It can also be integrated with a number of enjoyable exercise and recovery activities, and provide a good basis for cross-curricular work, for example, a ‘healthy bodies’ week. Practical activities such as this will capture pupils’ attention and involve them.
Resource 3 tells you how to measure heart rate, and gives some further information about heart rate, age and exercise to help you with Activity 2.
Case Study 2: Measuring heartbeats
Mrs Gwala explained to her pupils how to measure their heartbeats by holding their left wrist with the middle fingers of their right hand and counting the pulses. She asked them to practise this for a few minutes. Her pupils were very excited to do this – none of them had felt their pulse before. Mrs Gwala made sure that every pupil could find the pulse, either at the neck or the wrist. They all measured their pulses whilst sitting and noted this down, or remembered it.
She then asked them to stand up and sit down quickly ten times and then feel their heartbeats again. The pupils were surprised to see that they had become faster. She asked them to count their heartbeats for 10 seconds and then multiply by 6 to get the rate per minute.
Mrs Gwala asked the pupils to think why these changes might happen and listed their ideas on the board, e.g. they needed more energy. She was pleased with their thinking and saw them trying this out in the playground during break time.
Activity 2: Measuring heart rates after exercise
Before the lesson, make sure you can measure your heart rate at your neck and wrist (see Resource 3). Practise showing your family and friends how to do this before you try it with your class!
- Show your pupils how to feel the pulse at the neck and wrist, and make sure every pupil can feel the heartbeat in at least one of these two locations using the middle finger.
- Begin the lesson by telling your pupils that they are going to do an experiment. During the experiment they must sit completely still, and in absolute silence.
- Using your watch (or any clock that shows seconds), ask pupils to find their pulses, and then count how many beats they feel during one minute. Ask them to write down their heart rates but not to talk.
- Next, try some moderate exercise (e.g. walking for two minutes) and ask them to take their pulses again.
- Wait a minute and ask them to take their pulses again. Record the results
- They could then do other exercises, for example skipping or running, and then measure their heartbeats again and record their results.
- Ask all pupils to list on the board their resting heartbeats after walking and after skipping.
- Discuss with them the different results they have for each activity: for example, why were their pulses higher after skipping rather than walking?
3. Planning to teach for understanding
Understanding the importance of ‘units’ and the ability to read from scales are central to effective work in measurement. Later sections in this module will deal with length, weight and time: for each, it is important for pupils to understand the correct unit, and how to read correctly from the scales on measuring instruments. This part explores how you can plan activities to help pupils develop these skills. By using practical activities related to their everyday lives, pupils will see a purpose to the work and be more interested.
Case Study 3: Planning the next steps for pupils’ understanding of measuring
Mrs Gwala had spent some time working on different units of measure with her pupils. She felt that they were now getting confident in reading from the scale on their rulers, and from the weighing scales she had brought from home. They had talked about centimetres and millimetres and could show these on their rulers, and explain the relationship between them. They knew about local distances between towns, and that these were measured in kilometres. Mrs Gwala was pleased with the progress that had been made, and wanted to make sure the pupils could now see that ‘milli-’, ‘centi-’ and ‘kilo-’, could be applied to all measurements and units. (See Resource 4: Units of measurement.)
She decided to do this through ‘nonsense’ measures – making up playful units, and asking questions about them (see Resource 5: Space and measure for examples of such nonsense questions). After her pupils had grasped what she was doing, she allowed them to make up their own ‘nonsense measure’ questions, which they enjoyed greatly. Mrs Gwala was sure at the end of this that they knew well what ‘milli-’, ‘centi-’ and ‘kilo-’ meant, because they were able to explain the differences in their discussion.
Key Activity: Planning an observation lesson on measurement
Plan this activity with at least one other teacher at your school.
- Make a list of all the measuring devices you have access to that could be brought into the school (such as rulers, weighing scales, measuring jugs or spoons, etc.). Devices that have a scale are particularly useful. How do people selling vegetables in the local market measure what the customer wants? (For advice about collecting resources, see Key Resource: Being a resourceful teacher in challenging circumstances.)
- Think of activities that will allow pupils to practise using these devices and recording measurements, to develop their confidence and accuracy.
- Think about how you will introduce key terms: units, measurement, scale, distance, weight, volume, time, and what your pupils will do to understand and remember these terms.
- Decide how you will organise your pupils, how much time to allow and the resources you will need to carry out these activities.
- Plan your lesson, making sure that, as well as recording the ‘number’ from the device or scale, pupils also record the units and what is being measured (e.g. distance, weight, volume, time). See Key Resource: Planning and preparing your lessons.
Carry out this lesson. If possible, ask the teacher who helped you plan the activity to observe all or part of the lesson, and discuss it with you afterwards. What worked well? What was difficult? Were there any unexpected outcomes? How could you assess your pupils’ understanding of how to measure?
Resource 1: A measurement mind map
![]() Example of pupils' work
Example of pupils' work
Measurements that are common to the five situations shown in the mind map below are:
- length, surface or solid size;
- weight;
- capacity;
- time.
Resource 2: How mind maps can help mathematics teachers and pupils
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
Mind maps can help mathematics teachers to:
- plan topics and lessons in a way that is logical and systematic;
- identify and plan activities;
- introduce new concepts to pupils in interesting ways;
- promote better understanding of concepts;
- focus pupils’ attention on key aspects of a topic;
- help pupils prepare for tests and examinations;
- organise information that pupils are able to identify and relate to;
- help find out pupils’ misconceptions;
- assess pupils’ understanding of concepts and topics;
- plan extra support for some pupils.
Because concept maps can be drawn by pupils themselves, they are a useful tool for pupil-centred education.
Mind maps can help pupils to:
- summarise their knowledge of a topic and give an overview;
- help order topics according to their importance and relevance;
- link new ideas with previously learned material;
- show prior knowledge of a topic;
- reduce doubt so that the pupil knows what to study and what to leave out.
Resource 3: Heart rate
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
Heart rate is a term used to describe the frequency of the cardiac cycle. It is considered one of the four vital signs. Usually it is calculated as the number of contractions (heartbeats) of the heart in one minute and expressed as ‘beats per minute’ (bpm).
When resting, the adult human heart beats at about 70 bpm (males) and 75 bpm (females), but this varies. However, the reference range is nominally between 60 bpm (if less, termed bradycardia) and 100 bpm (if greater, termed tachycardia). Resting heart rates can be significantly lower in athletes. The infant/neonatal rate of heartbeat is around 130–150 bpm, the toddler's about 100–130 bpm, the older child's about 90–110 bpm, and the adolescent's about 80–100 bpm.
The body can increase the heart rate in response to a wide variety of conditions in order to increase the cardiac output (the amount of blood ejected by the heart per unit time). Exercise, environmental stressors or psychological stress can cause the heart rate to increase above the resting rate.
Measuring heart rate
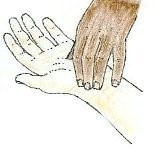
The pulse rate (which in most people is identical to the heart rate) can be measured at any point on the body where an artery is close to the surface. Such places are wrist (radial artery), neck (carotid artery), elbow (brachial artery), and groin (femoral artery). The pulse can also be felt directly over the heart. (Remember, never use your thumb to measure your pulse rate, because thumbs have a pulse rate of their own.)
It is also possible to measure heart rate acoustically, by listening to the sounds the heart makes while beating. These sounds can be listened to using a stethoscope.
Resource 4: Units of measurement
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
| Term | Meaning | Weight | Length | Volume |
| unit | The basic measure | gram (g) | metre (m) | litre (l) |
| kilo- | 1,000 times the unit | kilogram (kg) | kilometre (km) | - |
| centi- | 1/100 part of the unit | - | centimetre (cm) | centilitre (cl) |
| milli- | 1/1,000 part of the unit | milligram (mg) | millimetre (mm) | millilitre (ml) |
Units of time
- 1 minute = 60 seconds
- 1 hour = 60 minutes
- 1 day = 24 hours
- 1 week = 7 days
- 1 fortnight = 2 weeks
- 1 year = 12 months = 52 weeks = 365 days
How do you think these traders at a market in Knysna measure their goods?

Resource 5: Space and measure
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils

Acknowledgements
Grateful acknowledgement is made to the following sources:
Other
Resource 3: Heart rate: Original source: Wikipedia (Accessed 2008)
Resource 5: Space and measure: Original source: http://www.bbc.co.uk (Accessed 2008)
Every effort has been made to contact copyright holders. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Section 2: Measuring and handling time
Key Focus Question: How can you help pupils to understand and measure time?
Keywords: time; clock; sundial; history; mixed-ability; cross-curricular; practical activities
Learning Outcomes
By the end of this section, you will have:
- used practical activities to enhance your skills in mixed-ability teaching;
- considered the benefits of cross-curricular teaching in measuring time;
- developed your skills in managing an active classroom and resourcing it well.
Introduction
In order for pupils to understand time, they need to develop an awareness of time – past, present and future. This raises the question: How can pupils be helped to both tell the time and understand the passing of time through practical ‘hands on’ learning activities?
In this section, we consider a number of ways to do this, working in groups or pairs. As a teacher, you need to think ahead and plan activities. Collecting resources over time, such as card and paper that you can recycle to make models, is a good idea and will help you with the following activities.
1. Using group work to discuss ‘time’
A good introduction to telling the time is to first discuss the many ways people used to tell the time before the invention of clocks. You could ask your pupils how they think they might be able to tell the time today, without using clocks. Exploring these ideas first and listening to their answers will provide you with evidence of their current understanding. This will help you to judge how much they have learned after undertaking some activities about time.
Case Study 1: Exploring ways we used to tell the time
Mrs Tokunbo is a teacher in a primary school in Nigeria. She planned to teach ‘time telling’ to her pupils. She wanted to begin by helping them all to understand the need for a standard way of telling time.
First, she asked them to tell her what they thought about how to tell the time and listed these ideas on the board. She discussed other ways of telling the time long ago, including marked candles, sundials and sandglasses. For each of these methods of time telling, she asked pupils to think of what it would be like to depend upon such a method, and what problems it might cause. (See Resource 1: Ways of measuring time long ago for examples of what Mrs Tokunbo told her pupils.)
Activity 1: Discussing time telling in groups
Begin your lesson by asking your pupils to think of ways people tell the time without a clock and write down all their ideas on the board. You may need to suggest some examples, such as the rising and setting of the sun, the opening and closing of flowers like Etinkanika, or examples in Resource 1, Resource 2: Water clocks and Resource 3: Sundials).
Put them into groups of four or five and ask them how they know what time of day it is. Then ask them to discuss how reliable they think each of these methods are. Ask the groups to report back and have a class discussion, writing up relevant comments, of reliable ways to tell the time.
2. Cross-curricula practical work
‘Some people can tell what time it is by looking at the sun. But I have never been able to make out the numbers’ (Attributed to a primary pupil).
You may find it helpful to work together with the history teacher to explore how time was measured in different cultures throughout history. This could become activity-based – your pupils will probably enjoy experimenting with some of these ancient methods of time telling, such as making a candle clock or sundial. It will show your pupils that mathematics is – and has always been – important in many areas of life and study.
Using other experts in your classroom will help you learn more about a subject and will motivate your pupils. The teacher in Case Study 2 takes this approach.
Case Study 2: Using other experts to help teach time
Mrs Lengasha wanted to teach her pupils about time. She began by telling them stories of how people in her father’s village used to tell the time of day and how they knew when to arrange ceremonies and events. She asked them if they knew how the length of the shadow cast by a pole was used to determine when to do certain activities and the time for observing Muslim prayers.
Mrs Lengasha asked the history teacher to help by explaining how time was measured long ago. The history teacher told them about birds that sing at certain periods of the day or night, like cocks that crow in the morning, and of the relationship between the rainy and dry seasons and clearing-sowing-harvesting times. She told them of how some people used the moon to tell the time over a month.
By working with the history teacher, Mrs Lengasha showed her pupils that mathematics is not an isolated subject, and she herself learned some new examples and ideas about time that she did not know before. (See Resource 1, Resource 2, and Resource 3 for some examples.)
Activity 2: Measuring time using a sundial or shadow clock.
Before the lesson, collect some sticks and chalk. You could also read Resource 3 to learn more about sundials.
- Familiarise your pupils with sundials (or shadow clocks as they are sometimes called) and how they work.
- Ask each group of pupils to make simple sundials using card, a pencil or stick and some plasticine/mud (or put the stick in the ground).
- Use the plasticine/mud to hold the stick up on the card, and place the sundials outside. Ask pupils to mark the stick’s shadow at certain times of the day – ‘School begins’, ‘Maths class begins’, ‘Break time’, ‘Lunch time’ and so on, throughout the day.
- At the end of the day, compare the dials. Discuss how the shadow has moved. Can the pupils explain why?
They could use themselves as sundials by standing in the same position at certain points in the day and observing what happens to their shadows. Ask them to share their results and list the changes they notice about their shadows.
3. Using local resources to teach telling the time
There are several important facts pupils need to know about time (see Resource 4: Units of time), but one of the most challenging aspects for young children is often being able to ‘read’ a clock face. The use of practical ‘clock hands’ activities should help pupils to be able to read a clock and tell the time.
Once you have a clock or clocks, begin with times that are easier, gradually moving on to the more difficult times:
- ‘on the hour’ (o’clock);
- quarter past, half-past, quarter to the hour;
- five minute intervals;
- one minute intervals.
Case Study 3 and the Key Activity give examples of how you could do this.
Case Study 3: Telling the time
Mrs Ondieki wanted her pupils to be able to practise setting and reading different times from a clock face. She decided the best thing to do was to ask her pupils to make cardboard cut-out clock faces that they could practise with. She asked pupils to help her collect enough cardboard for every four pupils to be able to make quite a large clock face, and two hands for it.
When they had enough, she asked her pupils to cut out circular clock faces and hands from their cardboard; and showed them how to number them on the board, making sure they had the 12, 3, 6 and 9 at the key points. Mrs Ondieki had bought some ‘split pins’ to hold the hands on the clock faces.
Mrs Ondieki then explained to her pupils how they should use the clocks, starting first with telling the hours (one o’clock etc.). She showed the pupils a particular time on her own cut-out clock and they made their clocks say the same time. They worked in small groups, helping each other. (See Key Resource: Using group work in the classroom.)
They used the clocks they had made for several weeks, until Mrs Ondieki was sure that all her pupils could tell the time confidently. Every day, she also brought to the classroom a little alarm clock. She looked at this with her class at different times of the day to see what time it was.
Key Activity: Telling the time
- Collect the materials and make cardboard cut-out ‘clock faces’ with your pupils.
- Begin with whole-class teaching to help pupils see how the hours and minutes work.
- When pupils have some confidence in this, you may ask pairs or small groups to challenge each other: either saying a time, and asking their peers to show it on the clock face, or making a time on a clock face, and asking their peers to say what time is shown.
- Ask them, in groups, to make a list of the key things they do during the day, including the times they do them. You may have to help younger children. You could do a picture for the time.
- At the end of the lesson, or in the next lesson, ask them to draw clock faces in their books, and put in a time and then write down the time in words for each clock. (If you can, have one or two small round objects that pupils can draw around to save time.)
Resource 1: Ways of measuring time long ago
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
A story about using the crowing of the cock to tell the time
Mr Ali is a village petty trader. He takes his wares to nearby villages on their market days. He normally treks to the villages. To know when to start his journeys, he used to listen to the crow of the cock early in the mornings; that tells him it is morning and he would set off. But one day, the cock crowed too early. Mr Ali thought it was morning and set off. On getting to the road, he found that it was still very dark and for a long time he had to travel alone in the dark. He also got to the market too early and had to wait for a long time before other people arrived. From that day, Mr Ali concluded that depending on cock crows to know when it is morning is not always reliable.
Original source: http://inventors.about.com (Accessed 2008)
Resource 2: Water clocks – ways of measuring time throughout history
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
Water clocks were among the earliest timekeepers that didn't depend on the observation of celestial bodies. One of the oldest was found in the tomb of the Egyptian pharaoh Amenhotep I, buried around 1500 BCE. Later named clepsydras (‘water thieves’) by the Greeks, who began using them about 325 BCE, these were stone vessels with sloping sides that allowed water to drip at a nearly constant rate from a small hole near the bottom. Other clepsydras were cylindrical or bowl-shaped containers designed to slowly fill with water coming in at a constant rate. Markings on the inside surfaces measured the passage of ‘hours’ as the water level reached them. These clocks were used to determine hours at night, but may have been used in daylight as well. Another version consisted of a metal bowl with a hole in the bottom; when placed in a container of water the bowl would fill and sink in a certain time. These were still in use in North Africa in the 20th century.
More elaborate and impressive mechanised water clocks were developed between 100 BCE and 500 CE by Greek and Roman horologists and astronomers. The added complexity was aimed at making the flow more constant by regulating the pressure, and at providing fancier displays of the passage of time. Some water clocks rang bells and gongs; others opened doors and windows to show little figures of people, or moved pointers, dials and astrological models of the universe. In the Far East, mechanised astronomical/astrological clock making developed from 200 to 1300 CE. Third-century Chinese clepsydras drove various mechanisms that illustrated astronomical phenomena. One of the most elaborate clock towers was built by Su Sung and his associates in 1088 CE. Su Sung’s mechanism incorporated a water-driven escapement invented about 725 CE. The Su Sung clock tower, over 30 feet tall, possessed a bronze power-driven armillary sphere for observations, an automatically rotating celestial globe, and five front panels with doors that permitted the viewing of changing manikins which rang bells or gongs, and held tablets indicating the hour or other special times of the day. Since the rate of flow of water is very difficult to control accurately, a clock based on that flow could never achieve excellent accuracy. People were naturally led to other approaches.
Original source: http://inventors.about.com (Accessed 2008)

In Ctesibius's clepsydra from the 3rd century BC, the human-shaped hour pointer ascends as water flows in. Outflow drives a series of gears that rotate a cylinder bearing hour lengths appropriate for each day's date.
Resource 3: Sundials
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
The Egyptians formally divided their day into parts something like ours. Obelisks (slender, tapering, four-sided monuments) were built as early as 3500 BCE. Their moving shadows formed a kind of sundial, enabling people to partition the day into morning and afternoon. Obelisks also showed the year’s longest and shortest days when the shadow at noon was the shortest or longest of the year. Later, additional markers around the base of the monument would indicate further subdivisions of time.
Another Egyptian shadow clock or sundial, possibly the first portable timepiece, came into use around 1500 BCE. This device divided a sunlit day into ten parts plus two ‘twilight hours’ in the morning and evening. When the long stem, with five variably spaced marks, was oriented east and west in the morning, an elevated crossbar on the east end cast a moving shadow over the marks. At noon, the device was turned in the opposite direction to measure the afternoon ‘hours’.
In Europe, during most of the Middle Ages (roughly 500 CE to 1500 CE), technological advancement virtually ceased. Sundial styles evolved, but didn’t move far from ancient Egyptian principles.
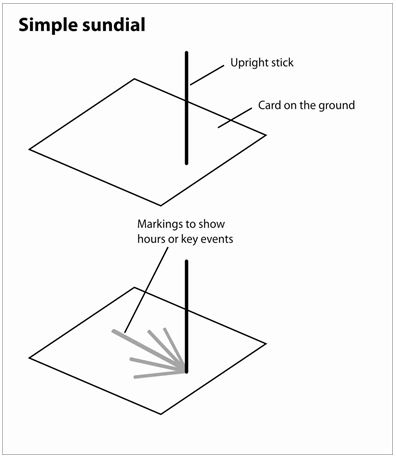
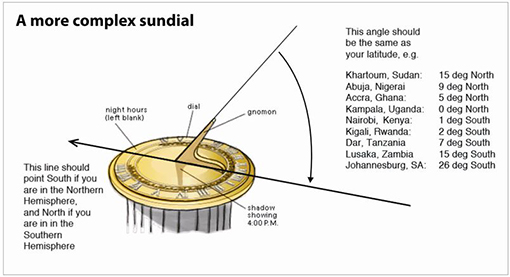
Original source: http://inventors.about.com (Accessed 2008)
Resource 4: Units of time
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
Time
|
Many timetables and digital watches use 24-hour clock time. Use this scale to change between 12-hour and 24-hour time. |
 |
Remember:
|
Here is a way to remember how many days there are in each month. Start by counting January on the first knuckle of your left hand and February as the gap between the knuckles. 
|
Original source: http://www.bbc.co.uk/ schools (Accessed 2008)
Acknowledgements
Grateful acknowledgement is made to the following sources:
Other
Resource 1: Ways of measuring time long ago: Original source: http://inventors.about.com (Accessed 2008)
Resource 2: Water clocks: Original source: http://inventors.about.com (Accessed 2008)
Resource 3: Sundials: Original source: http://inventors.about.com (Accessed 2008)
Resource 4: Units of time: Original source: http://www.bbc.co.uk/ schools (Accessed 2008)
Every effort has been made to contact copyright holders. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Section 3: Discussing data
Key Focus Question: How can pupils collect, collate and understand data?
Keywords: survey; data collection; data analysis; interpretation; pie chart; bar chart; pictogram; histogram; line graph; scatter graph
Learning Outcomes
By the end of this section, you will:
- be familiar with a range of different data sets that pupils can usefully collect for analysis;
- have developed your knowledge of graphically representing data;
- have developed and used a structured question approach to assess your pupils’ understanding.
Introduction
There are three core aspects of working with data: collecting data (using what pupils can do already and new methods to count things); recording data; analysing and presenting data. In all these activities, pupils themselves must play the major role.
The focus in this section is practical: pupils will collect data themselves, decide how best to represent it and analyse it. Through whole-class discussion, decisions are made by the pupils themselves, with guidance from you.
This section will help you plan and carry out these activities with your pupils, working with real ‘first hand’ data gathered in the classroom.
1. Organising surveys to collect data
Pupils are often more interested in working with data that they have collected themselves – they know what the numbers are describing, and where the numbers came from. Surveys help pupils to understand the concept of data collection and pupils are encouraged to continue collecting interesting data outside school.
Organising your class into groups so that everyone is able to contribute is important. Whole-class discussion can be used to share the data the different groups have collected.
Case Study 1: Using group surveys to gather data
Mrs Kazulu in Uganda decided to have a completely practical lesson and divided her class into three groups (if you have a big class you may need more groups – see Key Resource: Working with large classes). Her pupils were going to undertake small classroom surveys to collect data. She chose surveys that were relevant to the pupils themselves, asking one group to find out the number of siblings in their families, another to find out the number of letters in their names and the third to find the number of pupils from different districts in their class.
Mrs Kazulu drew a template like the one shown in Resource 1: Tally chart on the board. She gave her pupils time to copy her chart into their exercise books. She then asked them to work, one group at a time, going round the class and asking their survey questions in pairs.
Later, all groups shared their data and were asked to display it in some way in the classroom. Mrs Kazulu would use the data collected in future lessons.
Activity 1: A whole-class survey
Before you begin, show your class how to do a tally (see Resource 1). Ask them why they think this might be a useful technique.
Explain to your class that they are going to do a survey about birthdays. Ask them to suggest the best way to organise the list of the different months of the year. Then go round the class, asking each pupil to call out the month of their birth and let each pupil record the information as it is being called out.
Next, ask one pupil for each month to count up the birthdays and put in the total.
You could extend this work by setting an individual homework task, such as to survey the favourite sport or drink of family or friends. In the next lesson, discuss what the data tells you. Ask your class to think of other data they could collect like this and let them have another go at practising these skills.
What other ways could you organise your pupils to collect such data?
2. Interpreting and creating charts in groups
Collecting data is only part of some investigations, as it may need to be analysed and displayed to understand it better or to share the information with others. Pupils can show their data by using pictographs, pie charts, bar graphs, histograms or line graphs. It is important that pupils know which chart or graph is appropriate for which set of data, and so your examples should be clear. An overview of different kinds of charts is given in Resource 2: Charts and graphs.
Again, you will use data from the pupils’ own experiences but it is also a good idea to bring examples to class from newspapers, magazines and government publications.
Helping pupils understand the different kinds of chart takes time and you will need to plan several activities on each method to develop their understanding.
Case Study 2: Interpreting charts
Mrs Kunda teaches at a school in Mbale. She wanted to make sure her pupils could interpret simple charts before going on to produce charts of their own. She brought to schools some examples of pie charts, bar charts and line graphs (Resource 2).
First, she showed the class one of each type and, using some questions she had prepared beforehand, she checked that the pupils were able to understand the information that each one presented.
She then put the class into groups and gave out other charts. She wrote a few simple statements on the board, and told the groups to decide whether each one was true or false, according to the information in the charts. As the groups did the activity, Mrs Kunda walked around and listened.
When they had finished, Mrs Kunda checked the answers with the whole class, and explained one or two things that they had found difficult. In doing this, she introduced the idea that different types of chart are suitable for different types of information. Then she praised the class for their good work.
Activity 2: Creating charts
Before doing this activity, use Resource 1 and Resource 2 to familiarise yourself with different kinds of chart. Use Resource 2 to make sure you understand the uses and key teaching points for each chart type.
- Write the words ‘pie chart’, ‘bar chart’ and ‘line graph’ on the chalkboard and remind pupils what each type looks like.
- Copy the data in Resource 3: Data sets on the board, and get pupils to suggest which type of chart (pie chart, bar chart or line graph) would be most suitable in each case for presenting it. Use questioning to indicate the main features and uses of each type of chart.
- For each set of data, construct a chart on the board with the help of the pupils. (Draw the main outline and ask pupils to come out in turn and add to the chart. Ask the class for feedback each time.)
- In the next lesson, give out similar data and ask pupils to make charts individually.
3. Assessing understanding
This final part is on analysis and interpretation of data once it has been displayed. It will enable you to assess the success of your teaching (for more information, see Key Resource: Assessing learning).
Using information from the science teacher or another subject teacher shows that data collection and analysis is important across the curriculum; it also allows you to work with other teachers and gain support. Case Study 3 and the Key Activity show how your pupils can use new data and how you can use this to assess their understanding.
You may decide to use a structured question approach (see Resource 4: Structured questions) for your assessment, so that you can find out exactly how much each of your pupils has learned.
Case Study 3: Assessing understanding of data handling
Mr Kaluba wanted to make sure his pupils were confident at handling and interpreting data. He also wanted to show them what information they could get from their charts.
He asked the head teacher to provide numbers of pupils in each class in the school and asked his pupils to use this to draw a chart that showed the data well. He asked pupils to work in pairs to help each other with this task. Each pair had to agree on the best kind of chart to use.
Mr Kaluba asked them to note the title, the units used, the scales, what the axes represent, the highest and lowest points and any patterns in the chart, and to write a few sentences to explain what the chart showed them.
Mr Kaluba was pleased with their response and felt that his lesson had been successful. He displayed the pupils’ charts on the classroom wall.
Key Activity: Assessing data analysis and interpretation
To assess how well your pupils analyse and interpret data, you can use a structured question approach with questions that gradually get harder. This means starting with easy ones that all pupils can answer, moving on to less easy ones that can be answered by the majority of the pupils and including a last one which can be answered only by the more able pupils.
- Write the data on the board or on a piece of manilla paper (some example data is given in Resource 5: Kano’s rainfall).
- Write the questions on a separate sheet of paper.
- Show the chart and questions to the class. Explain they are to work on their own, drawing a chart using the data and then answering as many questions as they can.
- Give the class one lesson to do the activity.
- Collect in and mark their work.
- Next lesson, give feedback to the class about what they did well and where they need support and say how you will do this.
Resource 1: Tally chart
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
Making tally marks is a useful way to quickly count things in different categories. It involves making a mark or placing a store for each item counted in the particular group. The chart below shows a chart started for siblings in a class of 56 Primary 4 pupils. Each bundle of marks IIII represents five children.
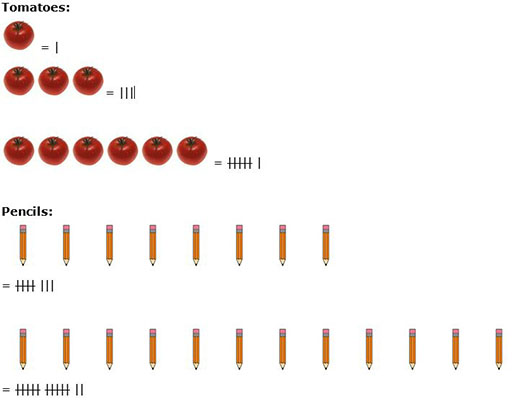
Resource 2: Charts and graphs
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher

Key: 1 - 1991, 2 - 1993, 3 - 1996, 4 - 1998
Resource 3: Data sets
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
Set 1
Proportion of Zambian men employed in 2005: 86%
Proportion of Zambian women employed in 2005: 74%
People in rural areas of Zambia who can get safe water: 28%
Set 2
Main language groups in Zambia, 2000
Bemba 30.1%
Nyanja 10.7%
Tonga 10.6%
Lozi 5.7%
Chewa 4.9%
Nsenga 3. 4%
Tumbuka 2. 5%
Numbers of people in main towns 2000
Lusaka 1,085,000
Ndola 374,000
Kiywe 364,000
Chingola 147,000
Mufulira 122,000
Set 3
Pupils attending secondary school 1991–1998
1991: 20%; 1993: 23%; 1996: 20%; 1998: 23%.
Visitors to Zambia 1990–2001
1990: 141,000; 1995: 235,000; 2001: 492,000.
Resource 4: Structured questions
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
A structured question is one that has three parts.
- Part 1 is easy and can be answered by all pupils.
- Part 2 is a bit more difficult but can be answered by the majority of pupils.
- Part 3 is more difficult and tests the more able pupils.
Here is an example.
Alice and Mary are having an argument. Alice says that it is hotter this week than it was last week. Mary thinks it was hotter last week. Here are the temperatures for the two weeks.
| Mon | Tues | Wed | Thurs | Fri | Sat | Sun | |
|---|---|---|---|---|---|---|---|
| Week 1 | 22ºC | 21ºC | 19.5ºC | 23ºC | 23ºC | 23. 5ºC | 22ºC |
| Week 2 | 18ºC | 19ºC | 23. 5ºC | 25ºC | 26ºC | 24ºC | 22ºC |
- a) Draw the temperature for both weeks on the same line graph, using different colours for each week. (Part 1)
- b) Which week showed the highest temperature? (Part 2)
- c) Which week showed the lowest temperature? (Part 2)
- d) Find the mean temperature for each week. (Part 2)
- e) Find the range of temperatures for each week. (Part 2)
- f) In some ways Alice is right and in some ways Mary is right. Explain. (Part 3)
Original source: The New Uganda Primary Mathematics Pupil’s Book 7
Resource 5: Kano’s rainfall
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
| Month | Average rainfall (mm) |
|---|---|
| January | 0 |
| February | 0 |
| March | 3 |
| April | 10 |
| May | 69 |
| June | 117 |
| July | 206 |
| August | 310 |
| September | 142 |
| October | 13 |
| November | 0 |
| December | 0 |
Acknowledgements
Grateful acknowledgement is made to the following sources:
Other
Resource 4: Structured questions: Original source: The New Uganda Primary Mathematics Pupil’s Book 7
Every effort has been made to contact copyright holders. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Section 4: Working with weight
Key Focus Question: How can practical work be used to teach the measurement of weight using inexpensive resources?
Keywords: Standard units; grams; kilograms; practical work; balances; extension; differentiation; groups; demonstration.
Learning Outcomes
By the end of this section, you will have:
- helped pupils develop their understanding of weight by using progressive practical activities;
- explored ways to establish pupils’ understanding of the need and use of standard units for weight;
- explained different ways to organise your class.
Introduction
When exploring weight with pupils it is important to use a lot of practical hands on activities in the early stages so that they are able to build up mental models which will help their understanding in later stages. In this section you will plan ways to introduce your pupils to the concept of weight by following three stages:
- comparing weights of two or more objects by holding them at the same time
- estimating and measuring weight of objects using non-standard units such as stones
- measuring and comparing the weight of objects using standard units
Central to this work is the use of simple balances and using standard units that can be made from cheap and readily available materials, to enable practical group work and active learning.
1. Doing practical work in groups
Estimation is an important skill in both mathematics and science and a useful skill to cultivate for all pupils. Simple balances can be made with very modest resources that allow pupils to approach measuring and estimating weight through practical investigation. You may like to make simple balances and plan and carry out these activities jointly with a science teacher in your school. This can be done by helping pupils to compare and contrast weights in different ways.
Case Study 1: Estimating weight
Mrs Nkumu in Nigeria was on a teachers’ course at her local district offices and as part of the day’s lesson on numeracy the facilitator told the following story to them. Then she asked them what they thought the girls knew and what would they do next with these pupils if they were in their class.
‘Two girls, Ranke and Ade, were discussing the quantity of popcorn in two packets, A and B which looked the same shape and size. Ronke picked up the packets one after the other and was surprised that B felt heavier than A. She told Ade that B appeared to be heavier than A. Ade decided to put the two packets in the two pans of a simple balance. (See Resource 1: Simple balance). She observed that on the scale, packet B went down and so B is heavier than A. Ronke was right.’
The teachers worked in pairs and devised activities that encouraged estimation of heavier/lighter, then using a balance or scales to test their ideas. Each pair tried their lesson out with their class and reported back next session.
Mrs Nkumu found that her class enjoyed the lesson but that she did not have enough different objects for the pupils to use. Next time she said she would spend more time collecting objects and she would use smaller groups of 4-6 rather than over 10 each.
Activity 1: Comparing weight
You will need 5 simple balances (see Resource 1) to carry out this activity and 5 sets of common objects e.g. stones, balls, tins, bottle tops etc that could be used with the balances.
Write instructions for your pupils on the board (see Resource 2: Worksheets) and show the class what you want them to do using any two objects.
Ask them to estimate which is heavier by giving the objects to 2 pupils to answer.
Now ask a pupil to test their idea out by putting them on the pan and let them decide.
Ask them which is the heaviest object and why they think so.
Organise your pupils into 5 groups, giving each group a set of objects and a balance. Ask pupils to find which object is heavier by estimating its weight and then by using the balance. (See Key Resource: Using group work in the classroom)
Ask them to fill in a table of their results to share with the class to see if everyone agrees.
You could challenge older or more able pupils to see if they can order their objects from heaviest to lightest before testing. How could they test their answers using the simple balance?
2. Introducing units to compare weights
When developing understanding of the idea of weighing it is better if non-standard units are used to measure first. If pupils compare and contrast weights against non-standard unit bottle tops or beans they will quickly understand this is not sensible as the weight of different bottle tops and seeds vary. This is made easier by making sure they have sufficient experience weighing objects against different non-standard units.
Only when pupils understand the need for a common unit should the introduction of standard units like grams or kilograms begin.
Case Study 2: Using a ‘standard’ unit to measure
Lizzy, a Primary school teacher, felt that having taught her pupils how to use a simple balance to compare weights of objects, they should now compare the weight of any object with that of a given chosen ‘standard’ object.
She assembled different objects and chose dry beans to be her chosen measure. Using the balance she asked two pupils to place an object on one pan and put enough beans on the other until it balanced. They counted the beans for each object and recorded their results.
Next she used some longer beans and weighed the same objects and recorded these results. She talked with the class about the difference in numbers between the two kinds of bean and how difficult it was to compare the weight of a stone and wood if one person used one set of beans and the other used the bigger beans.
Activity 2: Data presentation
Before doing this, read Resource 3: Pupil instructions for weighing activity and collect together the following resources – enough for your size class.
- simple balances
- collect objects of similar weights to use as measures (e.g. bottle tops and beans)
- objects of different weights to measure (e.g. small bottles, tins or stones).
You could just collect enough for one group and have each group take turns to do the activity while the others do different work.
Write the instructions for the groups on the board and explain what they have to do.
Resource 4: Traditional weights used in Ghana. These are examples of Akan weights used in trading. Notice that they are fashioned very beautifully.
(See Key Resource: Using group work in the classroom)
At the end, ask them to compare how it was different using beans or bottle tops to measure the weight, rather than just comparing pairs of objects. Note their answers on the board. Ask if they think this is a fairer way to measure.
Ask pupils to list the objects in order from heaviest to lightest – is this harder or easier than before? Why?
3. Being resourceful
The previous activities should have shown your pupils that ‘standard units‘ of weight are needed because without these it is not possible to accurately compare or know how much something weighs. This next part explores how you can introduce terms and develop their understanding of kilogram (kg), and gram (g) (1000 gram = 1 kilogram). You may want to bring bags of sugar and rice to class, to show their weight is recorded in grams or kilograms and for them to feel the actual weights or make some mock ones i.e. plastic bags filled with sand, stones etc to the correct weight. If you can, borrow a pair of scales to do this.
If you do not have access to calibrated weighing scales or weights at school, it may still be possible to make approximate measurements of weight using your simple balances, and using some every day objects that have their weight on them to test them against. The second focus in this part is on understanding the terms gram and kilogram and being able to convert one to the other. This kind of activity should only be undertaken when pupils are confident at weighing in grams and kilograms.
Case Study 3: Using homemade standard units
Mr. Adu wants his pupils to estimate, measure and compare weights of 1 object in grams and kilograms. He asked permission from a secondary school science department to use their balances to make bean-bags weighing 100g, 50g and 10g (using different coloured cloth for each weight). He asked some of the parents who work in the local sewing shop to help him sew several sets for his class.
He demonstrated the weighing of objects in grams using the improvised weights and a simple balance, and then asked pupils to weigh objects to the nearest 10g, and record their results in a table.
| Object | Weight |
|---|---|
The pupils were very enthusiastic and weighed nearly everything they could find in the classroom. Mr Adu listened to their talk as they weighed and was pleased to hear them using the correct terms easily
Key Activity: Weighing in grams
Before the lesson, collect a number of objects that have their weights shown – tinned or packet foods and other goods (you only need the wrapper, not the whole good). Try to have enough to give each group of pupils at least two or three labels. It would also be good to have some labels for weights in kilograms as well as grams.
Ask groups to write down the name of the product, and its weight – ensure that they include the correct units (grams or kilograms). They could do this by using the actual bags and putting them in order on their table. Pupils could arrange and re-arrange the packages by weight from highest to lowest or lowest to highest or sort into groups:
- > 500 grams or
- < 500 grams
Then ask pupils to convert each weight from kilograms to grams or vice versa.
When they have finished ask each group to swap their sheets with another group and they can check each others answers. Remind them that 1000 gram = 1 kilogram.
Discuss with your pupils why they might need to be able to convert weights in their everyday lives.
Display their work on the wall to show each group their achievements.
What did the groups learn and how do you know this? You could ask them to tell you what they think they have learnt.
Resource 1: Simple balance
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
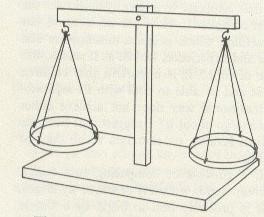
Resource 2: Worksheets
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
- One member of the group picks up and feels the weight of two objects, e.g. a stone and a bean, one after the other. Which feels heavier? Complete the table below.
- Another member now uses the balance to compare the weights and completes the table
- Repeat this for all the objects, comparing two objects at a time, allowing each member of the group to participate.
- Pin your table on the wall and look at each other's results.
| Objects | Which feels heavier | Which weighs heavier on balance |
|---|---|---|
| the ball and a bean | the ball | the ball |
| a bean and a stone | the stone | the bean |
| a bean bag and a stone | ||
| ||
|
Resource 3: Pupil instructions for weighing activity
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
- Put the object to be weighed, say 1 milk tin, in the left scale pan of the balance. Place one bean in the other scale pan. Which is heavier?
- Add more beans one at a time, in the scale pan on the right until the two sides balance. How many beans do you require for this?
- Repeat using bottle tops instead of beans.
- Repeat (1) and (2) for each of the objects to be weighed.
- Record your observations in the form of the table below
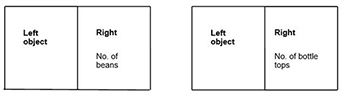
- Find out how many bottle tops weigh as much as 10 beans.
- Find out how many beans weigh as much as 10 bottle tops.
Resource 4: Traditional weights used in Ghana
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher

http://www.metmuseum.org/ search-results?ft=Traditional+Akan+weights&rpp=10&pg=2 (Accessed 2008)
Acknowledgements
Grateful acknowledgement is made to the following sources:
Photographs and images
Traditional Akan weights: http://www.metmuseum.org/ search-results?ft=Traditional+Akan+weights&rpp=10&pg=2 (Accessed 2008)
Every effort has been made to contact copyright holders. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Section 5: Investigating distance
Key Focus Question: What practical and imaginative approaches can you use to develop pupils’ understanding of distance?
Keywords: measurement; length; distance; comparison; active; practical; group; pair; investigative; proof
Learning Outcomes
By the end of this section, you will have:
- developed ways of teaching measurement of length in a more pupil-centred way;
- developed your ability to organise, support and assess practical investigations around distance.
Introduction
This section will help you develop pupils’ understanding of estimating, measuring, drawing, experimenting, constructing, interpreting and calculating lengths and distances.
Investigations can be done in class, individually or in groups. They can also be done at home by individual pupils, and either be presented to the whole class verbally or be formally as written work. Investigations are based on having an idea or a phenomenon that you want to find out about. To do this, you undertake various tasks in order to find answers to your questions. Investigations can include practical work, but can also take the form of research as you search books etc. for answers. For further information about investigation see Key Resource: Using investigations in the classroom.
1. Organising an investigation
Any investigation needs to be planned and conducted carefully, otherwise the results might be incorrect or unreliable. In Activity 1 you will look at a statement that needs to be shown to be right or wrong. Make sure your pupils have all they need before they start an investigation, and that they understand the task before they begin. Your role is to support them as they work by asking questions to stimulate their thinking and encouraging them to develop their ideas.
Case Study 1: Using questions to prepare for a practical investigation
Mrs Mwakapenda in South Africa wanted to give her pupils a practical investigation on length to find out who was the tallest or shortest in the class.
She prepared some questions for them to ensure that they understood the task properly. She began her lesson by discussing the questions with the whole class (see Resource 1: Sample questions). She was aware that the investigation was not just about measuring. It was also about collecting and recording data. She wanted to make sure her pupils understood exactly what it would involve.
After the investigation, Mrs Mwakapenda was very pleased with what her pupils had achieved. They had shown that they knew how to organise an investigation. They carried out a fair test and measured the distances well, too.
Activity 1: Who can jump the furthest?
Begin by asking your pupils to consider the following statement and discuss (in groups of four) how they would investigate whether it is true.
‘A tall person can jump further than a short person.’
Each group needs access to a tape measure or ruler or some other means of measuring e.g. string or rope. Discuss how they might answer the question and agree on a process. This might be like this:
- take two measurements for each person and measure everyone in the group;
- measure height by standing against a scale on a wall which you made before the lesson;
- the jump must be a ‘standing’ jump – the person stands on a line, and then jumps as far as they can;
- measure the length of the jump using a tape measure or string etc.
Ask the groups to discuss how they can show their results (see Resource 2: Two ways to check). Ask them if their measurements agree with the statement. If not, can they rewrite the statement to match their results?
2. Letting pupils plan their investigations
When exploring a topic such as measuring, it is important not to rush on to new concepts but to give pupils time to consolidate their learning and practise newly learned skills. This section provides more ways to explore pupils’ understanding and abilities to measure length in different contexts.
Here, you will ask pupils to make comparisons between measures and think about any links. By using the same groups for a series of activities, you can discover whether they see the similarity between the investigations and are able to use the data and the strategies they used before.
Case Study 2: Organising pupils’ own investigations
Mrs Baguna decided to undertake a measuring task with her class but provide less guidance than she had before. She wanted them to be more independent and to use the skills learned from previous tasks. She decided she would listen carefully as they discussed how to proceed and find out who was volunteering to do tasks. She was interested to know who realised they could use the previous knowledge and ways of working for the new task.
She thought carefully about what task to set. The head teacher had talked of moving the school fence and school gate on one side of the grounds to a place he said was nearer, to help save money. Mrs Baguna was not sure it was nearer and she decided this was a real problem to use with her class.
She set the problem in the morning and told her pupils they could work on it until the end of the day. They also had to do their language work but she said they could choose in which order to work. As she only had two long tape measures borrowed from the education offices, it limited the number of groups that could work with these at any one time. They could use other ways to measure, such as rope or string. She was pleased with how well they organised themselves and, as they worked, she noticed who understood the problem and how to solve it. All the groups agreed that the new site for the path was much nearer. She then asked them to work out how much money would be saved from the path.
They took their investigation to the head teacher who was very pleased with the information.
Activity 2: Investigating height against arm-span
Begin by telling your pupils that you have another investigation for them to do in the same groups as before.
Ask them to find out if this statement is true:
‘Your height is the same as the distance between your fingertips with your arms outstretched.’
Ask them to discuss in their groups:
- How they could check these statements?
- What are they going to be measuring?
- What units of measurement should they use?
- How will they organise the work?
- How will they record their results?
Next, ask them to do the investigation together, or at different times (depending on your resources), and go around and listen to them as they work, supporting them if they are having difficulty. Ask them to show how they worked out the answer. Display their answers.
Discuss with them what you have observed about how they worked as groups.
How can you help them work better in groups? (See Key Resource: Using group work in the classroom.)
3. Assessing understanding of length
It is important that pupils have a real-life ‘feel’ of what different lengths mean and are able to estimate and measure the length or height of an object. This is a very useful skill in real life. For example, will a tree fall on our house if it is chopped or falls down? To assess whether they have this ‘feel’, you can use a question to solve on paper that requires them to use their understanding or give them a final investigation about a real object, such as that in the Key Activity.
When the task is complete, encourage your pupils to find out more about the indigenous trees of your country and have a go at measuring a large tree near your school if there is one. Working in this practical way will build their confidence in dealing with length.
Case Study 3: Assessing understanding of length
Mrs Juma from Tororo Rock wanted to find out if her pupils had a real understanding of different lengths, so she designed a paper activity that they had to do individually to assess this. She copied the activity onto the board (see Resource 3: Question on length). She asked her pupils, who were Primary 6, to work on their own and think carefully about the answers before they filled in the gaps. She collected their books and looked at their answers.
Mrs Juma realised that many of her pupils had not got a real feel for length yet and so she decided to do more practical activities. She asked them to measure the school grounds but they had to estimate the length of each side first and record this. Each group took it in turns to do the measuring as she only had one long tape. She had made a large table of the key measurements and each group put in their measurements as they finished. She did not display this until all groups had finished so they would not be influenced by others’ results. (She planned to use this data later for a SST lesson to produce a scale map of the school site.)
When all pupils had completed the measuring, she discussed the variations in their measurements with them and then asked them why this was so. They were able to suggest some good reasons such as starting at different points and not holding the tape straight.
Key Activity: How big is the big tree?
Read Resource 4: Big tree in Budongo Forest before you plan for the lesson, but think how you might adapt this to your pupils’ needs. You will need to find a very long tape measure.
If possible, take your pupils outside to where there is a lot of space; otherwise, use a large hall to try out the activities. You will also need about 60 pupils of average 1 m height and so you may decide to combine with another class. Work with the whole class together and ask guiding questions to help them solve the problem.
Read the following extract about the ‘Big Tree’ to the class.
- ‘In Budongo Forest there are huge old mahogany trees. Some are 60 m high and have a circumference of 6 m or more.’
Show them the picture as you start your lesson and then undertake the activities in Resource 4.
When you have finished outside, bring your pupils inside and ask them to answer the questions in Resource 4 to assess their understanding.
Next lesson, ask them to make a display of all their measuring activities and invite other classes to come and see their work.
Resource 1: Sample questions
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
- What do you understand by the term ‘height of a person’?
- How are you going to measure yourself?
- Should you have shoes on or off, while measuring?
- Should you lie down or stand up against the wall?
- What about those with long hair, should they squash it down?
- Where should you measure from?
- What should you measure with?
- How accurate should you be?
- How do you use a ruler or tape measure?
- How should you collect the measurements?
Resource 2: Two ways to check
![]() Background information / subject knowledge for teacher
Background information / subject knowledge for teacher
- One way of checking that the statement is true is to make a table with two columns, one for the heights of the pupils going in order from the tallest down and the other for the lengths of the corresponding jumps. Only if the order is the same is the statement true.
- Another way is to make a mark with a cross on a grid using square paper with the pupil’s height on the horizontal axis and the length of jump on the vertical axis. Only if the result of the crosses is a straight line is the statement true.
Resource 3: Question on length
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils
Some pupils in Primary 3 measured different things in school. These are the measurements they wrote down.
- a. 4 metres
- b. ½ metre
- c. 19 metres
- d. 1½ metres
Below is a list of the things they measured. Match each length or height against the most likely object.
- Florence, who is in Primary 3
- The length of the school building
- The length of the teacher’s table
- The height of the classroom
Resource 4: Big tree in Budongo Forest
![]() Teacher resource for planning or adapting to use with pupils
Teacher resource for planning or adapting to use with pupils

The height of the Big Tree
Remind your pupils that the height of the tree is 60 m. Ask them:
‘Do you think if all the pupils here were to balance on each other’s heads you would eventually reach to the top of this tree?
That would not be easy and so what else can we do? Yes, we could try lying down instead.
Let’s do that.’
Ask about ten pupils to lie down and ask another pupil to measure and see if that is enough.
Now ask: How many pupils do you think it will take?
Add more pupils until how many it takes to make 60 m is reached.
Finally, ask someone to describe how tall the Big Tree is.
The circumference of the Big Tree
We are told that the circumference of the tree is 6 m. Ask your pupils:
‘How many pupils do you think it would take if you wanted to make a ring around the tree, with fingers touching?’
Try it by asking one pupil to measure 6 m. Then form a circle and count the pupils – this will give you an idea of the circumference of the tree.
Now try these questions with your group:
-
Before this activity I thought 60 m was:
- a. As tall as my school building
- b. As tall as a mountain
- c. As high as a tall tree
- d. As tall as a telephone tower
- e. Hadn’t thought about it
-
It would take the following number of classmates to make a ring around the giant tree in Budongo Forest:
- a. At least 7
- b. At least 6
- c. At least 5
- d. At least 4
- e. At least 3
-
1 m in length is approximately:
- a. The span from the tip of an average person’s nose to their fingers with arms outstretched
- b. The height of an average person
- c. The length of a small table
- d. The height of a cow
Acknowledgements
Every effort has been made to contact copyright holders. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.