Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated dimanche 8 mars 2026, 09:00
Module 2 : Étude de la forme et de l’espace
Section numéro 1 : Exploration des formes
Question clé: Comment pouvez-vous aider les élèves à développer et utiliser un vocabulaire mathématique pour les formes ?
Mots clés: objet ; forme ; géométrie ; langage ; classification ; activités ouvertes
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- utilisé des activités de tri ouvertes pour explorer la connaissance des formes;
- exploré des manières pratiques de faire découvrir aux élèves le langage ou « registre » des termes mathématiques ;
- utilisé des activités pratiques pour développer la compréhension des élèves et leur utilisation des descriptions mathématiques de formes géométriques de base.
Introduction
L'analyse des formes ou l’exploration de la géométrie avec vos élèves peut être très enrichissante. L’adoption d’une stratégie pratique et l’utilisation d’objets se trouvant dans l'environnement des élèves peuvent contribuer à motiver et intéresser les élèves.
Dans cette section, vous utiliserez des objets de la vie de tous les jours pour aider les élèves à développer d’importantes aptitudes de géométrie, comme la reconnaissance, la visualisation, la description, le tri, la nomination, la classification et la comparaison.
1. Exploration et classification des formes
Pour commencer, vous devrez rassembler un éventail de ressources pouvant être utiles pour les activités de cette section (voir la Ressource 1 : Utilisation de sacs mystères). Vous pouvez rassembler et conserver une boîte d'objets de ce type comme ressource permanente. Vos élèves apprécieront peut-être de vous aider à rassembler les ressources et de « rechercher des formes » dans la vie de tous les jours. (N’oubliez pas de faire l’éloge des élèves qui participent et de saisir l’opportunité de parler de la forme des objets qu'ils apportent.)
Étude de cas 1 : Planification de l’étude des formes
Des enseignants de mathématiques du primaire à Tsévié, au Togo, préparent un programme de travaux géométriques pour le trimestre. Dans le cadre de leur formation continue, ils souhaitent préparer de bonnes activités pratiques de géométrique pour leurs élèves.
Ils décident d’inviter un expert en éducation mathématique de l'établissement d'éducation supérieur voisin pour les aider à préparer leur programme. Cette enseignante accepte et suggère de commencer par une activité de tri. Ils doivent rassembler autant d’objets que possible, comme des boîtes vides, des bobines de fil de coton, des tubes de carton intérieurs de rouleaux de papier WC et des photos de formes différentes dans l'environnement: bâtiments, motifs (dessins) de tissus etc. Par deux, ils préparent une activité utilisant ces formes et l’essaient eux-mêmes.
De retour dans leur classe, les enseignants demandent à leurs élèves de les aider à rassembler des objets similaires. Lorsqu’ils en ont un nombre suffisant pour que les élèves travaillent en groupes de cinq ou six, chaque groupe ayant dix objets ou plus à trier, ils essaient les activités.
Les tâches consistent à placer les objets dans des groupes possédant des propriétés similaires, à enregistrer les propriétés communes et à enregistrer les objets ayant ces propriétés. Les enseignants sont surpris et encouragés par l’intérêt et la réflexion que suscite cette activité parmi leurs élèves.
Au cours de la réunion d’enseignants suivante, chaque enseignant présente un rapport sur ce qui s’est passé.
Activité 1 : Aider les élèves à trier des objets réels
Rassemblez autant d’objets de formes différentes que vous pouvez. Il vous faut au moins deux objets par élève. Vous pouvez aussi utiliser des photos de formes dans l’environnement.
- Répartissez la classe en groupes de cinq ou six élèves et donnez à chaque groupe une sélection d’objets (voir la Ressource 1).
- Expliquez en quoi consiste un « ensemble »: une collection d’éléments ayant des caractéristiques communes. Par exemple, la classe est un « ensemble » d’élèves qui ont un enseignant en commun – vous. Ce « grand ensemble » peut être divisé en plus petits ensembles. Par exemple, un ensemble de garçons et un ensemble de filles. (Si vous le souhaitez, vous pouvez séparer physiquement les élèves pour former ces deux ensembles et illustrer votre argument.)
- Expliquez aux groupes que vous leur avez distribué un ensemble d'objets différents. Vous voulez qu’ils classent ces objets en ensembles plus petits. Posez-leur la question suivante : Combien de manières différentes y a-t-il de trier ces objets en ensembles ? La tâche devient ainsi une tâche « ouverte » - n'indiquez pas le nombre d’ensembles ou de critères.
- Demandez-leur d’expliquer les raisons pour lesquelles ils ont trié les objets dans chaque ensemble.
- Pendant que les élèves travaillent, observez-les et écoutez leurs discussions au sein des groupes, en notant soigneusement ce qu’ils disent. Ceci vous aidera à déterminer ceux qui ont des idées claires et ceux qui en sont encore au stade d'exploration des idées.
- Demandez à chaque groupe de partager les manières différentes de trier les objets et notez les caractéristiques principales au tableau.
Vous pouvez utiliser une double leçon pour cette activité.
2. Introduire et développer le langage mathématique pour parler des formes
Après avoir présenté le concept du tri des objets et demandé aux élèves de décrire les caractéristiques en langage « de tous les jours », il est temps de développer une manière plus mathématique de décrire certaines caractéristiques des objets.
Dans tous les domaines d’activité, les personnes développent des mots et termes spéciaux pour décrire ce qu’elles font. Le langage spécial des mathématiques est parfois appelé le registre mathématique. Il faudra prendre le temps pour présenter le langage des formes aux élèves ; vous devrez intégrer cette activité à vos leçons au fil du temps. Quand vos élèves auront compris les concepts derrière les noms, le moment sera venu de leur présenter les mots mathématiques. Outre l’utilisation de ces mots en pratique, vous pourrez également demander à vos élèves de commencer à créer un « dictionnaire mathématique » pour les aider à mémoriser la signification de ces termes. La Ressource 2 : Un dictionnaire mathématique donne six exemples des types de mots que les élèves peuvent utiliser pour décrire les formes avec lesquelles ils travaillent.
Étude de cas 2: Utilisation de termes mathématiques pour trier des objets
Mme Johnson demande à ses élèves de trier une collection d'objets de formes différentes qu'elle a distribués. Certains élèves décident de trier les objets selon l'endroit où on les utilise à la maison: la chambre, la cuisine et la salle de bains. D’autres élèves examinent la ressemblance entre les objets. D’autres groupes ont des difficultés à décrire les caractéristiques de leurs objets, par exemples ils déclarent que certaines formes sont plates mais peuvent uniquement décrire les autres formes comme « pas plates ».
En rassemblant toute la classe autour d’elle, Mme Johnson examine certains de ces objets problématiques « pas plats » avec les élèves. Sans utiliser les termes mathématiques initialement, elle commence à indiquer certaines caractéristiques (courbes, bords et angles) et demande aux élèves de les décrire en utilisant leur propre vocabulaire. Ensuite, lorsque quelques élèves ont décrit ces caractéristiques et ont fait appel à tous les mots qu’ils peuvent utiliser, Mme Johnson commence à introduire les termes mathématiques corrects et définit avec les élèves comment ils pourraient décrire ces termes en utilisant leur propre vocabulaire. Elle explique qu’ils commencent à apprendre « le beau langage des mathématiques » (voir la Ressource 2pour certains termes à utiliser).
Mme Johnson prépare une grande feuille à afficher au mur et y écrit les nouveaux mots mathématiques accompagnés des définitions créées avec les élèves. Elle demande aux élèves de commencer à créer leur propre dictionnaire mathématique à la fin de leur cahier d’exercices, en dessinant des diagrammes pour montrer la signification de ces mots. Ils ajouteront des mots à ce dictionnaire au cours des leçons de mathématiques ultérieures.
Activité 2: Décrire les objets géométriques
- En utilisant une sélection d’objets rassemblés, regroupez les élèves autour de vous et montrez-leur certains des objets.
- Montrez-leur un objet avec une surface plane, puis un autre avec une surface bombée.
- Demandez aux élèves de choisir d’autres objets ayant des surfaces planes ou des surfaces bombées.
- Demandez aux élèves de réintégrer leur groupe et distribuez à chaque groupe une sélection d'objets.
- Leur tâche est de placer chaque objet dans l’un de ces quatre ensembles :
- toutes surfaces planes ;
- toutes surfaces bombées ;
- surfaces planes et bombées ;
- autres.
- Vous pouvez développer cette activité en introduisant deux autres termes : « sommet » et « bord » et en utilisant ces termes pour trier les objets.
- Réalisez un tableau de leurs résultats qui sera affiché dans la classe.
3. Utilisation du jeu des sacs mystères pour pratiquer et évaluer l’acquisition du langage mathématique
Une manière d’évaluer si vos élèves ont bien appris à comprendre et utiliser la langue de description des formes est l’utilisation de « sacs mystères » (voir la Ressource 1 pour avoir plus de détails). Un élève doit soigneusement décrire un objet caché dans un sac. L’élève doit utiliser les mots spéciaux qu'il a appris; les autres élèves doivent essayer de deviner quel est l’objet décrit. Les élèves doivent ainsi visualiser la forme se trouvant dans le sac et utiliser correctement les termes géométriques simples qu’ils ont appris pour « gagner » le jeu du sac mystère. Il est important d’organiser cette activité de manière à faire participer tous les élèves. En effet, si elle est bien faite, un plus grand nombre d’élèves apprendront mieux.
Étude de cas 3: Jouer au jeu du sac mystère pour pratiquer l’utilisation des termes mathématiques
Mme Johnson a fait des sacs en tissu assez grands pour que la main d'un élève puisse y entrer; elle a fermé le haut avec un cordon à coulisse.
Elle a mis l’un des objets de sa collection dans chacun des sacs, en choisissant soigneusement les objets pour obtenir des variations de formes.
Mme Johnson explique le jeu à sa classe et choisit l’élève qui va toucher et décrire la forme de l’objet du premier sac. Cet élève doit décrire l’objet en utilisant les mots qu’il vient d’apprendre. Les autres élèves doivent lever la main quand ils pensent savoir quel est l'objet. La récompense de l’élève qui devine l’objet correctement consiste à être la personne qui va toucher et décrire l’objet dans le sac mystère suivant.
Pendant l’activité, Mme Johnson vérifie que tous les élèves sont attentifs et autorise un seul élève à la fois à s’exprimer pour que tous les élèves puissent réfléchir à ce que dit chaque personne.
Activité clé : Utiliser un sac mystère pour réfléchir aux formes
Tout d’abord, préparez votre sac ou boîte mystère.Il vous faut un sac ou une boîte où vous mettrez un objet et dans lequel ou laquelle un élève pourra mettre la main pour toucher l'objet, sans le voir (voir la Ressource 1).
Vous pouvez utiliser un seul sac mystère pour toute la classe ou, si votre classe est nombreuse, plusieurs sacs pour permettre à plusieurs groupes de travailler en même temps. Ceci permet à plus d'élèves de participer.
Commencez alors le jeu.
- Un élève doit toucher l’objet dans le sac (ou dans la boîte) et, sans le sortir, le décrire très soigneusement aux autres. L’élève ne doit pas nommer l’objet.
- ll doit dire des choses comme « toutes ses surfaces sont planes, il a tant d’angles, il a tant de surfaces planes » etc.
- La description continue jusqu'à ce qu'un élève pense avoir deviné l'objet.
- Si la réponse est correcte, l’objet est sorti du sac et l’élève qui a deviné correctement est celui qui touche l'objet suivant (ne donnez qu'une chance à chaque élève).
Encouragez vos élèves à utiliser le vocabulaire appris dans les activités précédentes pour décrire les objets. Demandez-leur de les ajouter à leurs dictionnaires mathématiques.
Ressource 1 : Utiliser des sacs mystères
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Les sacs ou boîtes mystères, que vous (ou vos élèves) pouvez facilement confectionner (voir ci-dessous) peuvent être utilisés tout au long du programme pour développer les observations et les aptitudes linguistiques de vos élèves. En mathématiques, c’est un bon moyen d’aider les élèves à explorer les propriétés des formes et des objets. En science, vous pouvez explorer les textures des matériaux. L’utilisation d’un sac ou d’une boîte mystère est un excellent moyen de motiver les élèves car la participation au jeu, la nécessité d'écouter attentivement et le désir de deviner la bonne réponse les stimulent et les intéressent.
Suggestions d’objets pour les activités sur les formes
Vous pouvez utiliser différents cubes (dés, blocs), des prismes rectangulaires (boîtes, blocs en bois) des prismes triangulaires (coins en bois, boîtes de chocolats fantaisie), des sphères (boules), des pyramides (en bois ou en plastique), des cylindres (rouleaux de papier toilette, stylos, chevilles), des cônes (chapeaux de fête, cônes pour crème glacée). Vous pouvez aussi inclure un ou deux objets de forme irrégulière ou semi-irrégulière (pierres, coquillages, feuilles) pour susciter des discussions. Tous ces objets peuvent être collectés localement pour établir un lien entre les mathématiques et l’environnement.
Confectionner un sac mystère
Pour cette tâche, vous pouvez utiliser un sac en papier non transparent ou bien vous pouvez coudre un sac en tissu de 30 cm par 30 cm, ouvert à une extrémité. Le haut du sac doit pouvoir être fermé et ouvert pour y placer les objets et pour permettre à l’élève d'y mettre la main pour toucher l’objet ; vous devez cependant vérifier que personne d'autre ne voit ce qui se trouve dans le sac. Vous pouvez utiliser un élastique ou un cordon à coulisse pour fermer le haut du sac.
Confectionner une boîte mystère
N’importe quelle boîte en carton de taille moyenne peut être utilisée pour créer une boîte mystère. Vous devez découper une ouverture de la taille d’une main sur un côté de la boîte. Cette ouverture permet à un élève de mettre une main dans la boîte pour saisir l’objet et le toucher. Certains enseignants découpent deux trous pour que l’élève puisse mettre les deux mains dans la boîte. L’ouverture doit être placée loin des regards du reste de la classe pour que les autres élèves ne puissent pas voir ce qui se trouve dans la boîte.
Les règles du jeu Ce jeu consiste à cacher des objets intéressants et différents (que vos élèves connaissent) dans le sac ou la boîte mystère. Vous pouvez utiliser des bols ou pots de forme régulière, des outils ou même des boîtes alimentaires. | |
Un élève vient devant la classe et met la main dans le sac ou la boîte mystère pour toucher un objet. Il ne le sort pas et ne le montre pas aux autres élèves. L’élève réfléchit très soigneusement à des manières de décrire l’objet sans mentionner son nom. Il utilise le sens du toucher pour répertorier et décrire ses observations. Il doit rester très scientifique et mathématique. Il doit tenir compte des propriétés de l’objet. Il doit réfléchir soigneusement à la forme et à la taille de l’objet. Chaque fois que l’élève fait une observation, un autre élève de la classe a une chance d’essayer de deviner l’objet. Pendant que tout cela se déroule, l’enseignant peut prendre le rôle de scribe (ou secrétaire) pour enregistrer les observations et les inférences au tableau ou sur une grande feuille de papier. Seuls les points principaux sont notés. Le jeu se poursuit jusqu’à ce qu’un élève devine correctement l’objet. L’objet peut alors être extrait du sac ou de la boîte et montré au reste de la classe. Il est important de passer un peu de temps à parler de l’exactitude des observations – aptitudes de langage mathématique, efficacité des descriptions, aptitudes de communication et qualité des inférences. |  |
Ressource 2 : Un dictionnaire mathématique
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Il en existe de nombreux sur le marché. Celui de Stella Baruk
Dictionnaire des mathématiques élémentaires est de bonne qualité.
Voici quelques mots concernant la géométrie :
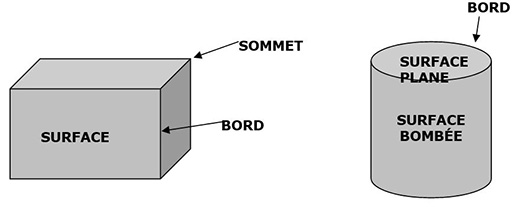
- Surface bombée
- Bord
- Surface
- Surface plane
- Sommet
Les élèves peuvent noter leurs propres définitions de chaque mot et les vérifier auprès de leurs camarades ou de vous s’ils ne sont pas sûrs que leur définition est correcte.
Section numéro 2 : Passage de la feuille au cube
Question clé: Comment pouvez-vous aider les élèves à « voir » et transformer mentalement des formes géométriques ?
Mots clés: réseaux ; géométrie ; visualisation ; transformation ; boîtes ; dés ; enquêtes
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- exploré des manières pratiques d’utiliser l’environnement local et des réseaux simples pour aider les élèves à comprendre les objets en 3D ;
- utilisé des enquêtes et des exercices de résolution des problèmes pour développer la réflexion de vos élèves à propos des différents réseaux pour créer des cubes ;
- utilisé des dés pour encourager la visualisation mentale et la transformation de réseaux cubiques.
Introduction
Imaginez que vous devez dessiner une forme sur une feuille de papier ; cette forme pourra être découpée et pliée pour former un cube. Sur la feuille, vous allez dessiner les six carrés qui seront pliés pour créer les six faces du cube. Pouvez-vous imaginer la forme que vous dessineriez sur la feuille pour créer le cube ?
Cela n’est pas facile à faire, car cet exercice mental exige deux aptitudes mathématiques importantes : la visualisation mentale (le fait de pouvoir « voir » dans votre esprit une image mathématique en deux dimensions (2D) ou en trois dimensions (3D)) et la transformation mentale (le fait de pouvoir « manipuler » ou modifier cette image d’une manière ou d’une autre).
Cette section explore des manières pratiques de développer ces aptitudes chez vos élèves lorsqu’ils créent des réseaux. (Un réseau est une représentation en 2D d’une forme en 3D, des lignes en pointillés représentant les pliures et des lignes continues représentant les coupures.) La manipulation d’un objet réel aidera vos élèves à visualiser les transformations de cet objet et à mettre en relation leur compréhension des formes et leur propre vie.
1. Organiser un travail d’investigation sur les formes 3D
Pendant que vos élèves travaillent, ils doivent vraiment avoir l’impression de réaliser une enquête, de résoudre le problème. En tant qu’enseignant, vous devez pouvoir prendre du recul et observer vos élèves prendre les commandes. Au début, vous aurez sans doute du mal à faire cela, mais si vous pouvez trouver un moyen d’organiser votre classe pour que les élèves aient assez d’espace pour réfléchir, parler et explorer, beaucoup d’entre eux vous surprendront par leur imagination et leur compréhension. Pour avoir un complément d’information, consultez la Ressource clé : Travail de recherche et d'investigation en classe.
Activité 1 et Étude de cas 1 explorent des manières de permettre à vos élèves de découvrir eux-mêmes les réseaux de différentes formes.
Étude de cas 1 : Étudier un réseau pour une boîte de conserve
Mme Nèmè au Togo travaille sur les formes. Elle emmène d’abord sa classe dans l’environnement local pour observer les différentes formes.
Le jour suivant, elle veut commencer sa leçon sur les réseaux en demandant à ses élèves de découvrir eux-mêmes un réseau simple.
Mme Nèmè leur demande de réfléchir à la manière de faire un plan en papier de certaines des formes qu’ils ont observées. Elle écoute certaines de leurs idées. Ensuite, après avoir demandé à ses élèves d’apporter une boîte de conserve (elle en apporte quelques unes elle-même pour ceux qui ont oublié ou qui ne peuvent pas s’en procurer une), elle leur pose la question suivante et leur demande d’en discuter en groupes de deux : « Votre boîte a été fabriquée à partir d’un morceau de métal plat. Imaginez que votre feuille de papier est un morceau de métal que l’on va transformer en boîte de conserve - quelle forme devez-vous découper dans le papier ? Pouvez-vous utiliser la boîte pour vous aider à dessiner cette forme sur votre feuille ? La Ressource 1 : Réseau d’une boîte de conserve (un cylindre) montre comment on peut plier un réseau en 2D pour en faire un objet en 3D.
Elle donne du temps aux élèves pour qu’ils essayent de résoudre ce problème. Mme Nèmè observe ses élèves pendant qu’ils travaillent et intervient uniquement quand elle voit qu’ils ont des difficultés.
Elle est très heureuse de constater qu’ils sont nombreux à pouvoir créer le réseau.
Activité 1 : Identifier le réseau d’une boîte sans couvercle
Pour cette activité, demandez à chaque élève d’apporter une boîte vide. Vous devez en amener quelques-unes vous aussi.
- Donnez à chaque groupe de quatre élèves de la colle ou du scotch et quatre feuilles de papier A4.
- Dites aux élèves qu’ensemble ils vont explorer comment créer une boîte de la même forme que la boîte (un prisme rectangulaire - voir ci-dessous) en utilisant une feuille A4 et en dessinant, en pliant et en collant.
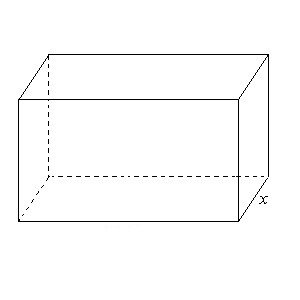
- Demandez-leur de travailler ensemble et de parler de la manière de procéder avant de commencer. Lorsque les groupes sont satisfaits de leur méthode, demandez-leur d’utiliser une feuille de papier pour tester leurs idées.
- Si certains groupes ont des problèmes, donnez-leur un indice en leur suggérant de défaire la boîte pour la mettre à plat.
- Circulez sans rien dire ; aidez les groupes uniquement lorsqu’ils ont des difficultés ou demandent de l’aide.
- Demandez à chaque groupe de montrer son travail à la classe.
- Pendant la leçon suivante, demandez aux élèves de décorer leur boîte et suspendez-les au plafond.
- Enfin, demandez-leur de dessiner leurs plans ou réseaux de la boîte qu’ils ont confectionnée ; affichez aussi ces plans.
2. Explorations de réseaux en groupes
Dans cette partie, vous allez aider les élèves à développer leur compréhension en passant des boîtes ouvertes aux boîtes fermées. Pour cela, il faut ajouter un couvercle à la boîte et expliquer les modifications devant être apportées au réseau.
Utilisez les mêmes groupes pour que les élèves puissent approfondir les idées collectives déjà trouvées. Si vous placiez vos élèves dans de nouveaux groupes pour cet exercice, ils devraient d’abord revenir sur les idées initiales, ce qui ralentirait le développement de nouvelles idées.
Dans cette partie, vous montrerez à vos élèves qu’il n’y a pas une seule réponse correcte mais de nombreuses réponses possibles. En ne leur fournissant pas trop d’explications, mais en leur posant des questions pour guider leur réflexion, vous leur donnez la satisfaction de découvrir les choses par eux-mêmes. Cela développera leur confiance en eux et leur donnera le courage d’essayer de nouvelles idées.
Étude de cas 2: Concevoir des réseaux de boîtes fermées
M. Akakpo est satisfait des progrès de ses élèves dans l’Activité 1. Il leur explique qu’en mathématiques certains mots ont un sens spécial. Par exemple, en mathématiques, le mot « réseau » est parfois utilisé pour désigner une forme plane (une forme plate, en 2 dimensions), que l’on peut plier pour former un objet en trois dimensions. Il demande à ses élèves d’ajouter ce terme à leur dictionnaire mathématique et de lui donner une définition. Comme ils ont déjà réalisé un réseau pour une boîte sans couvercle, il leur demande de créer le réseau d’une boîte avec couvercle. Il leur suggère d’examiner les réseaux déjà dessinés et de réfléchir à la manière d’ajouter un couvercle. M. Akakpo demande aux mêmes groupes de discuter ensemble de la manière d’ajouter un couvercle, et de dessiner le nouveau réseau. Il donne dix minutes aux groupes puis demande à chaque groupe de dessiner ses résultats au tableau.
Il demande alors à chaque groupe d’examiner les différents réseaux et de décider s’ils fonctionnent tous.
Activité 2: Quels réseaux peut-on plier pour créer un cube ?
Vérifiez que les élèves comprennent en quoi consiste un cube, puis demandez à des groupes de deux élèves de trouver autant de réseaux possibles pour un cube. Ils doivent d’abord dessiner chaque réseau, puis le découper et vérifier qu’il crée bien un cube, avant d’essayer de dessiner un réseau différent.
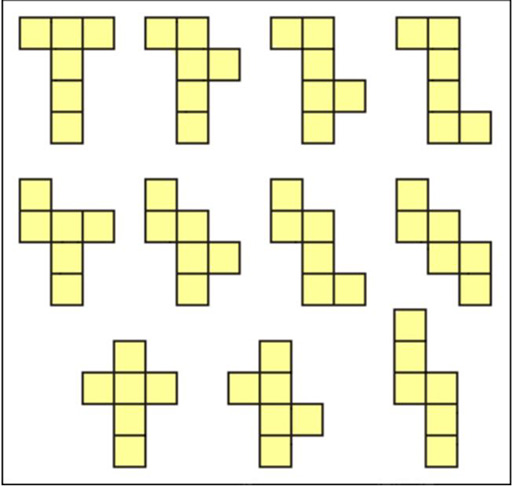
(Vous pouvez montrer un ou plusieurs exemples comme ceux ci-dessous pour les aider à commencer.)
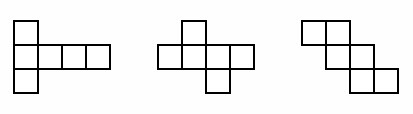
Vous pouvez organiser cet exercice sous forme d’un concours, en offrant une récompense au groupe qui peut réaliser le plus de réseaux pour des cubes (voir la Ressource 2 : 11 réseaux pour un cube).
Encore une fois, n’intervenez pas et ne parlez pas trop pendant cette leçon ; donnez aux élèves la liberté nécessaire pour explorer leurs idées et apprécier l’activité. Écoutez-les attentivement et identifiez les manières dont ils arrivent à résoudre leurs propres problèmes.
Affichez les cubes terminés et, si vous avez le temps, laissez les élèves décorer les cubes pour fêter leur réussite.
Discutez du nombre de réseaux différents identifiés par les élèves. Demandez-leur de créer un tableau des 11 possibilités d’un réseau pour un cube.
3. Développer la compétence de résolution de problèmes
Après avoir familiarisé les élèves avec les réseaux et créé des formes cuboïdes à partir des réseaux, vous allez maintenant utiliser des moyens pour aider vos élèves à visualiser et transformer mentalement ces réseaux. Une manière de faire ça est d’utiliser un dé. Une autre manière est d’observer les formes dans l’environnement.
Un dé est un cube spécial, car chaque surface porte un nombre unique, entre 1 et 6 ; les nombres des surfaces opposées donnent 7 lorsqu’on les additionne. Voir la Ressource 3 : Informations sur les dés.
Pour numéroter correctement les carrés d’un réseau cubique, avant de le plier pour en faire un cube, l’élève doit pouvoir visualiser mentalement la transformation de 2D en 3D. L’Étude de cas 3 et l’Activité clé explorent ces idées de différentes manières.
Étude de cas 3: Dessiner des réseaux pour différentes formes
Mme Yendoubé souhaite sensibiliser ses élèves à la présence des mathématiques dans la vie de tous les jours ; elle les emmène donc au marché voisin. Elle emmène du papier et des crayons et demande à ses élèves de chercher différentes boîtes. Elle leur demande de faire un croquis des boîtes de différentes formes. Certains élèves de Mme Yendoubé dessinent des boîtes de thon pour illustrer les boîtes cylindriques et des cartons pour illustrer des prismes rectangulaires.
Elle leur demande de préparer, au propre, à la maison des dessins des boîtes et des réseaux qu’ils pensent être corrects pour ces formes, car elle veut les afficher dans la classe. Les élèves sont très heureux de leur travail ; elle leur demande donc d’inviter leurs parents à venir voir leur travail. Mme Yendoubé sait qu’il est important d’avoir la coopération des parents car cela renforce le travail fait en classe.
Activité clé : Créer des réseaux de dés
Avant la leçon, rassemblez ou créez plusieurs dés que vous montrerez à votre classe.
Demandez aux élèves, en groupes de deux, de regarder un dé et d’examiner soigneusement les nombres - ils doivent pouvoir identifier que chaque face porte un nombre entre 1 et 6 ; vous devrez peut-être les aider à voir que les faces opposées donnent 7 lorsqu’on additionne leurs nombres. Donnez-leur le temps de vérifier si cette règle s’applique à tous leurs dés.
Distribuez maintenant à chaque groupe deux jeux de feuilles quadrillées 5 x 5 vierges. Demandez-leur de créer différents réseaux pour un dé : un réseau pour cube avec des nombres écrits sur les carrés, qui doivent respecter les règles ci-dessus. Lorsqu’ils pensent avoir résolu le problème, ils peuvent découper les réseaux et vérifier qu’ils ont bien créé des dés « corrects ».
Lorsque les groupes ont résolu le problème, ils peuvent écrire des numéros de dés sur certains des 11 autres réseaux pour cubes identifiés précédemment.
Demandez à chaque groupe de créer une affiche pour présenter les différents motifs de numérotation pour chaque réseau.
Vous pouvez développer cette activité en demandant à votre classe de créer un jeu de société sur le thème des formes, et d’utiliser leurs propres dés pour y jouer.
La Ressource 4 : Réseaude dés numérotés donne un exemple d’une solution correcte et un modèle permettant à vos élèves plus aptes de rechercher combien il y a de manières différentes de placer les numéros correctement sur le dé.
Vous pouvez utiliser une double leçon pour cette activité.
Ressource 1 : Réseau d’une boîte de conserve (un cylindre)
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Un réseau est une forme plane ou en 2D que l’on peut plier pour créer un objet en 3D. Voici le réseau d’une boîte de conserve, appelé cylindre.
L’objet en 3D ci-dessous (un cylindre) est créé en pliant le réseau en 3D.
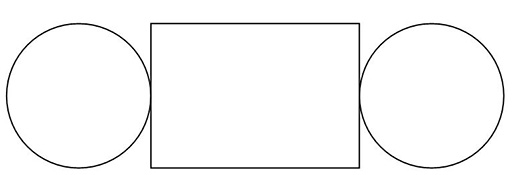
Un réseau en 2D
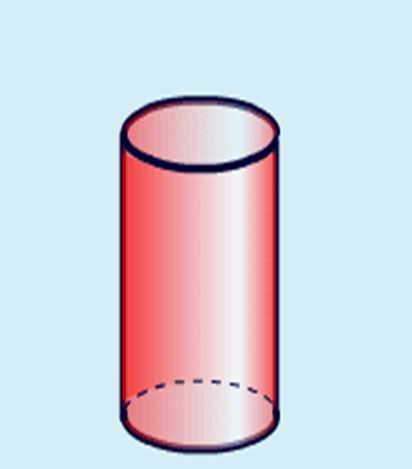
Un objet en 3D (un cylindre)
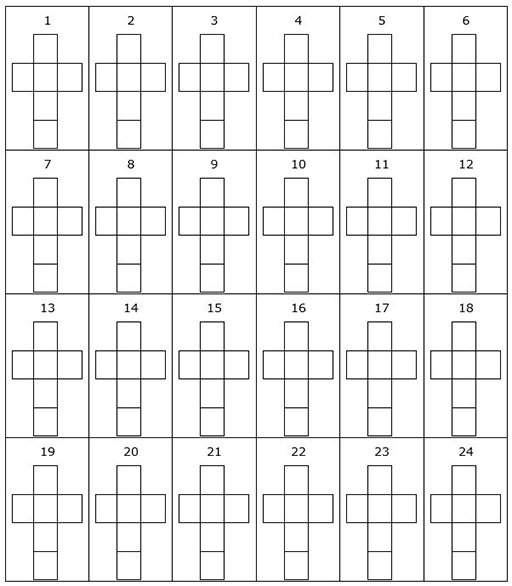
Ressource 2 : 11 réseaux pour un cube
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource 3 : Informations sur les dés
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
- Un dé est un cube dont chaque face porte un nombre entre un et six.
- La somme des deux numéros sur les faces opposées est toujours 7 ; les paires opposées sont donc :
- 1 et 6
- 2 et 5
- 3 et 4

Source: Dice, Wikipedia, Website
On peut utiliser des dés seuls pour jouer, ou bien avec un jeu de société lorsque les joueurs peuvent déplacer leur pion vers la fin du jeu après avoir jeté les dés. La première personne à atteindre la fin est le gagnant. Parmi ces jeux, citons « Le jeu de l’oie » et les « Petits chevaux » (voir Module 1, Section 1, Ressource 2 pour avoir les règles de ces jeux).
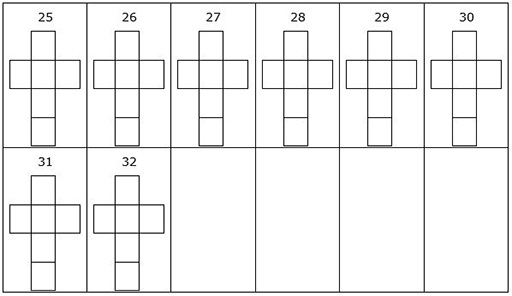
Ressource 4 : Réseau de dés numérotés
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Voici un exemple d’une solution correcte:
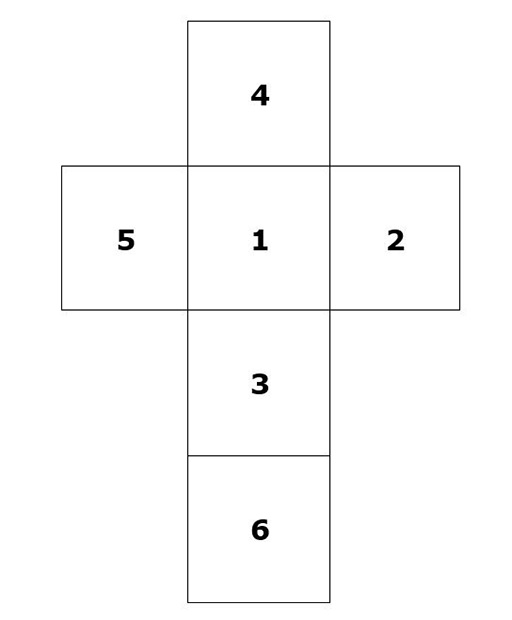
Numérotation des réseaux de dés
Combien y a-t-il de manières pour vos élèves de placer les numéros sur un réseau de dé en respectant les règles ?
Section numéro 3 : Exploration des formes en 3D
Question clé: Comment pouvez-vous utiliser des travaux pratiques pour étudier la relation entre les formes en 2D et en 3D ?
Mots clés: Polyèdre ; enquête ; motifs ; surfaces ; bords ; sommets ; polygones ; connaissance du sujet
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- développé vos propres connaissances sur les polygones réguliers (formes en 2D) et les polyèdres (objets en 3D);
- exploré des activités pratiques pour aider les élèves à étudier la relation entre les polygones et les polyèdres.
Introduction
Le processus de construction de solides géométriques réels représente une manière informelle et pratique pour les élèves de se familiariser avec les objets géométriques et de les comprendre.
Comme les élèves peuvent toucher les formes et les objets étudiés, ils se sentent plus aptes à réfléchir de manière abstraite. Si ces formes sont liées à des objets de la vie quotidienne, la réflexion et la visualisation des élèves s’en trouvent facilitées.
1. Travaux pratiques en groupes sur les formes 3D
Pour explorer et étudier les polyèdres, vous devez en avoir des exemples dans votre classe. Il existe plusieurs jeux de construction en plastique dans le commerce pour créer des objets en 3D, que vous pouvez apporter dans votre classe pour les utiliser, mais il est tout aussi facile de créer ces objets vous-mêmes avec des matériaux recyclables comme le plastique, le carton et le papier rigide. Si les élèves peuvent créer leurs propres formes, ils comprendront mieux leurs propriétés.
Vous pouvez utiliser des pailles en plastique, du fil à coudre et du fil de fer pour construire des « squelettes » de maquettes en 3D. En tant qu’enseignant, prenez l’habitude de conserver les objets pouvant être utiles en classe - par exemple, conservez toujours une paille quand vous achetez une boisson fraîche. Vous pouvez utiliser des réseaux déjà préparés de différents solides qui peuvent se replier pour les ranger facilement. Ils aideront les élèves à explorer la différence entre les formes en 2D et les objets en 3D.
Étude de cas 1 : Faire la différence entre les objets en 3D et les formes en 2D
Mme Yem, enseignante à l'école primaire de Glidji au Togo, souhaite que ses élèves prennent conscience de la différence entre les objets en 3D et les formes en 2D. Elle sait que c’est parfois un concept difficile pour eux.
Elle décrit les objets en 3D comme les objets « que l’on peut saisir, comme les livres, les stylos, les bureaux etc. » Elle explique que les formes en 2D sont les choses que l’on peut voir mais pas saisir. Une image d’un cheval sur une photo, le portrait d’une personne, ou même un carré dessiné sur du papier. Elle explique qu’on peut saisir la photo ou le portrait, mais on ne peut pas prendre le cheval de la photo ou la personne du portrait.
Elle invite alors les élèves à suggérer d’autres choses se trouvant dans la classe que l’on peut considérer comme 2D ou 3D.
Certains élèves sont très intéressés par cette distinction alors que d’autres ont vraiment du mal à croire qu’une feuille de papier ou une fenêtre sont des objets en 3D parce qu’ils sont « trop minces ».
Mme Yem décide de donner à ses élèves un devoir à faire à la maison. Elle leur demande de décrire à leurs parents ce qu’ils ont appris. Le devoir est d’apporter une liste d’au moins dix choses en 3D qui se trouvent à la maison ou dans les environs. Elle est convaincue que cela leur permettra de consolider le travail déjà fait en classe.
Activité 1 : Comprendre les formes en 3D ou polyèdres
Avant de donner cette leçon, vous devez rassembler ou créer des objets en 3D et les mettre dans un carton (voir la Ressource 1 : Formes régulières).
Répartissez les élèves en groupes de six à huit. Demandez à vos élèves d’examiner soigneusement les formes et objets se trouvant dans le carton. Demandez-leur les formes, comme des carrés et des rectangles, qu’ils reconnaissent sur les objets.
Donnez-leur le nom des objets:
- Prisme, par exemple cube, cuboïde, cylindre
- Pyramide, par exemple cône, sphère
Demandez-leur s’ils connaissent d’autres objets dans l’école et près de chez eux qui ressemblent à ces formes.
Expliquez-leur que tous les solides, à l’exception du cylindre et de la sphère, s’appellent aussi des polyèdres. Posez-leur cette question : « Pourquoi pensez-vous que les cylindres et les sphères ne sont pas considérés comme des polyèdres ? » Voir la Ressource clé : Utiliser l'explication et la démonstration pour favoriser l'apprentissage, qui vous donnera des idées.
Dites aux élèves que le mot polyèdre vient d’un mot grec qui signifie « un siège ».
Les prismes et les pyramides ont de nombreuses surfaces plates comme des sièges, alors qu’un cylindre n’est pas un polyèdre car il a une « surface » bombée.
Terminez l’activité en demandant à chaque groupe de compter les surfaces de chaque objet. Demandez aux élèves de noter leurs réponses dans leurs cahiers. Partagez les réponses de chaque groupe avec toute la classe.
Comme travail à la maison, demandez-leur de rechercher ces formes en rentrant à la maison, ou à la maison, et de vous présenter leurs résultats le lendemain.
2. Une approche interdisciplinaire pour motiver
Consultez la Ressource 2 : Photographie d’une pyramide. Les pyramides intéressent les élèves. Nous explorons ici comment visualiser différentes pyramides. L’enseignant de l’Étude de cas 2, en faisant un travail inter-curriculaire, a montré à ses élèves que les mathématiques ont un rapport avec d’autres disciplines scolaires et avec la vie réelle. L’Activité 2 examine les mathématiques des pyramides en demandant aux élèves d’en créer une en utilisant un réseau.
Étude de cas 2: Examiner les pyramides d’arachides pour motiver les élèves en mathématiques
Pour préparer sa leçon, M. Amadou souhaite faire participer d’autres enseignants et donner à ses élèves une expérience qui dépasse les mathématiques. Il parle à ses collègues qui enseignent les sciences humaines et art. Ceux-ci lui donnent une photo de pyramides de sacs d'arachides, à Maiduguri au Nigéria (voir la Ressource 2).
Il affiche la photo à un endroit où tous ses élèves peuvent la voir, et leur demande de lui dire ce qu’ils savent à propos de cette photo. M. Amadou crée une carte mentale de ce qu’ils savent sur la méthode de construction des pyramides. (Voir la Ressource clé : Utiliser les cartes conceptuelles et le remue-méninges pour explorer les idées.)
Ensuite, il les répartit en petits groupes pour parler des pyramides et noter leurs questions sur les pyramides. Il rassemble toutes leurs questions et trie celles qui concernent la structure des pyramides et leur forme.
Il donne à chaque groupe des pyramides qu’il a créées avec du carton (voir Réseau de pyramide dans la Ressource 3 : Réseaux). Il demande aux groupes de réfléchir à la forme et à la structure et aux caractéristiques communes, comme les côtés, les bords et les surfaces de chacune.
Il leur demande ensuite de réfléchir pour découvrir comment les personnes de Mandouri peuvent construire des structures aussi grandes que ces pyramides. Il leur montre de nouvelles photos de la méthode construction des pyramides qui intéressent beaucoup sa classe. Ceci conduit les élèves à demander à leur enseignant de sciences humaines et art de leur en dire plus sur les pyramides.
M. Amadou pense que cette association des mathématiques et des études sociales a motivé ses élèves dans leur travail mathématique.
Activité 2: Créer des pyramides en papier
Vous devez avoir des copies de la Ressource 3 : Réseaux, du papier, des ciseaux et du scotch ou de la colle. Si la quantité de fournitures ne permet qu’à un seul groupe de travailler à la fois, vous pouvez étaler cette activité sur une semaine.
Expliquez à vos élèves que les pyramides peuvent avoir une base comportant n’importe quel nombre de côtés - les plus simples ont des triangles équilatéraux sur les quatre surfaces, mais les pyramides peuvent aussi être créées avec n’importe quel polygone régulier comme base : les pyramides d’arachides ont des côtés triangulaires mais une base carrée.
Distribuez les réseaux de pyramides à base triangulaire et carrée et demandez aux élèves de les découper, les plier et les coller pour créer des pyramides en papier. Créez une présentation de ces pyramides
Ensuite, distribuez des pailles ou des allumettes sur le bureau de chaque groupe et demandez aux élèves de créer une pyramide avec ces matériaux, en s’aidant de ficelle ou de scotch. Circulez et aidez les groupes pendant qu’ils travaillent. Laissez-les partager les méthodes qu’ils ont utilisées pour bâtir leurs pyramides.
3. Des activités créatives et pratiques pour consolider les apprentissages
Dans cette partie, nous passons à une exploration plus formelle de différentes formes en utilisant des activités exigeant que les élèves fassent des observations attentives avant de créer eux-mêmes différents objets en 3D. La Ressource 4 : Les objets en 3Dfournit une synthèse utile de l’apprentissage des élèves jusqu’à présent.
Étude de cas 3: Transformer des polyèdres en mobiles
Mme Boko souhaite développer la compréhension de sa classe primaire du cours moyen 1ère année en leur faisant construire des polyèdres pour réaliser un nouvel ensemble de mobiles à suspendre dans sa classe. Elle demande à ses élèves de se mettre par groupes de six à huit et distribue à chaque groupe des ciseaux, du carton et de la colle. Elle demande à chaque groupe de créer 32 triangles équilatéraux, 6 carrés et 12 pentagones. Elle écrit les dimensions de chaque forme sur le carton.
Elle demande aux élèves de rechercher le nombre de polyèdres différents qu’ils peuvent créer avec leurs polygones en respectant ces règles :
- Utiliser un seul type de polygone à la fois pour créer le polyèdre.
- Tous les bords doivent se rejoindre.
Les élèves apprécient beaucoup cette activité.
Ensuite, elle leur distribue des réseaux de polyèdres réguliers et leur demande de les découper proprement, de les plier et de les coller pour créer des polyèdres (voir la Ressource 3). Ils s’aperçoivent que les formes construites sont identiques aux polyèdres qu’ils ont découverts.
Elle demande aux élèves s’il était plus facile de transformer les réseaux en polyèdres ou de partir des formes séparées. La plupart des élèves répondent que les réseaux sont plus rapides.
Activité clé : Caractéristiques des formes en 2D et objets en 3D
Commencez par consolider ce que les élèves ont appris dans les activités précédentes. Vous devez vous munir de votre carton de formes et objets, ainsi que de tableaux pour enregistrer les résultats (voir la Ressource 5 Enregistrer les résultats) ou demandez à vos élèves de dessiner les deux tableaux dans leurs cahiers.
Répartissez vos élèves en groupes de deux ou en petits groupes.
Distribuez-leur l’un des objets de votre carton de formes et demandez-leur d’examiner soigneusement la forme et de remplir le tableau aussi bien que possible.
Suggérez-leur de remplir une ligne à la fois. Demandez-leur de remettre leur forme dans le carton et d’en prendre une autre, jusqu’à ce qu’ils aient examiné chaque forme.
Après une durée appropriée, demandez à un groupe de présenter ses réponses à la classe concernant une forme. Circulez dans la classe jusqu’à ce que les caractéristiques de toutes les formes aient été présentées et que chaque groupe ait pu vérifier ses réponses par rapport à celles de tous les autres.
Demandez aux élèves s’ils ont remarqué des similarités dans leurs observations. Quelles formes et quels objets sont liés ?
Affichez leurs réponses.
Vous pouvez utiliser le jeu « Devinette des formes » de la Ressource 5 pour terminer ce sujet et évaluer leur compréhension pendant qu’ils jouent. Vous pouvez répartir la classe en équipes pour le jeu.
Vous devrez peut-être utiliser une double leçon pour cette activité.
Ressource 1 : Rassembler et créer des formes et objets
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Vous devez dessiner/réaliser des découpes en carton des formes 2D suivantes:
- Triangle
- Carré
- Pentagone
- Hexagone
- Heptagone
- Octogone
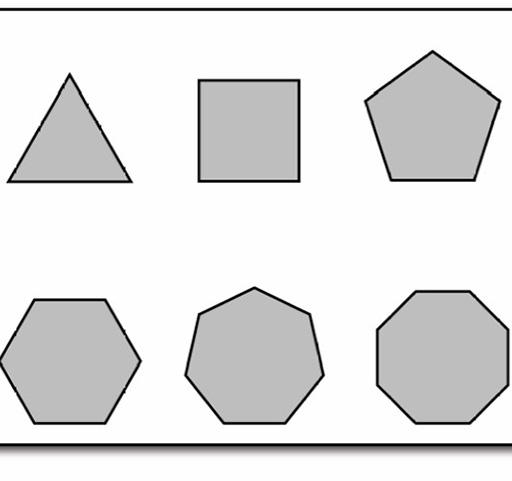
Vous pouvez maintenant passer aux objets en 3D.
Il vous faut rassembler ou fabriquer les objets en 3D suivants :
- une sphère
- un cube (un morceau de sucre ou un cube en allumettes
- des prismes rectangulaires (une boîte d’allumettes, une boîte à chaussures)
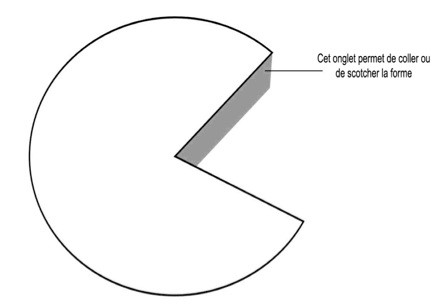
- un cône (vous pouvez découper et couper le réseau d’un cône fourni ci-dessous)
- des cylindres (le tube de carton d’un rouleau de papier WC, une feuille de papier roulée et collée)
Vous pouvez aussi créer des cubes, des pyramides ou des prismes avec su papier ou des pailles.
Ressource 2 : Photographie d’une pyramide
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves

Les pyramides de sacs d'arachides, à Maiduguri au Nigéria
Adapté de: Encyclopaedia Britannica Concise
Ressource 3 : Réseaux
![]() Utilisation par les élèves
Utilisation par les élèves
Voici des gabarits de différents objets en 3D que vos élèves peuvent créer.
Gabarit de tétraèdre
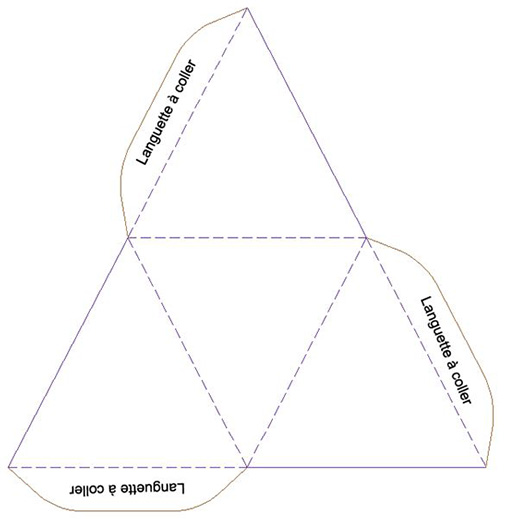
Gabarit de cube
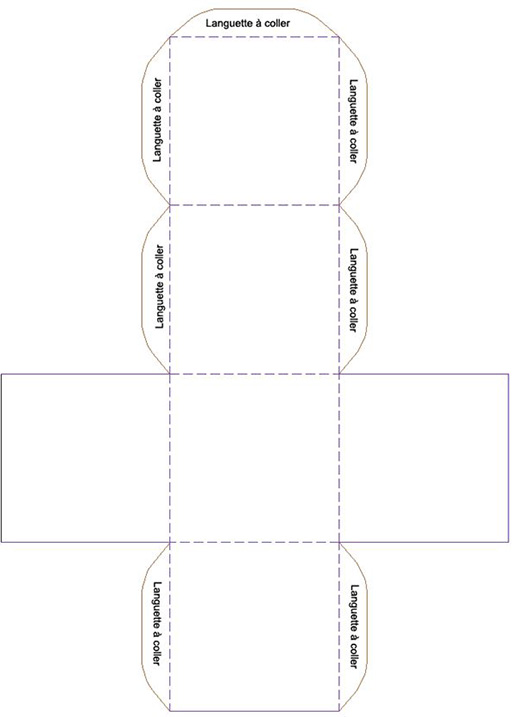
Gabarit d’octaèdre
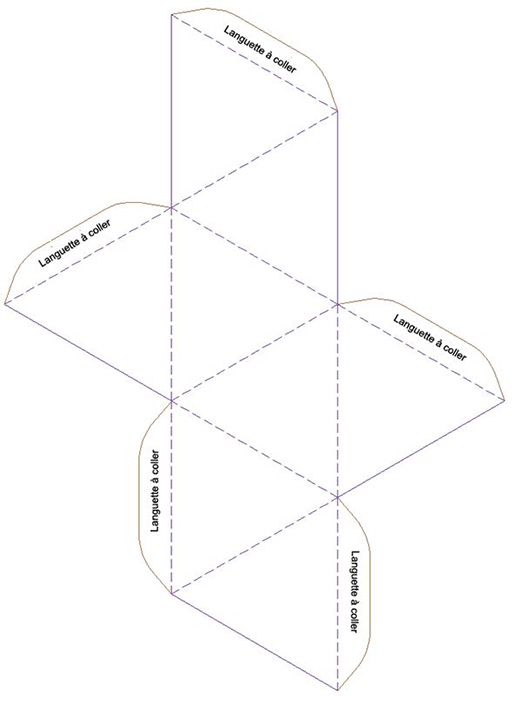
Gabarit de dodécaèdre
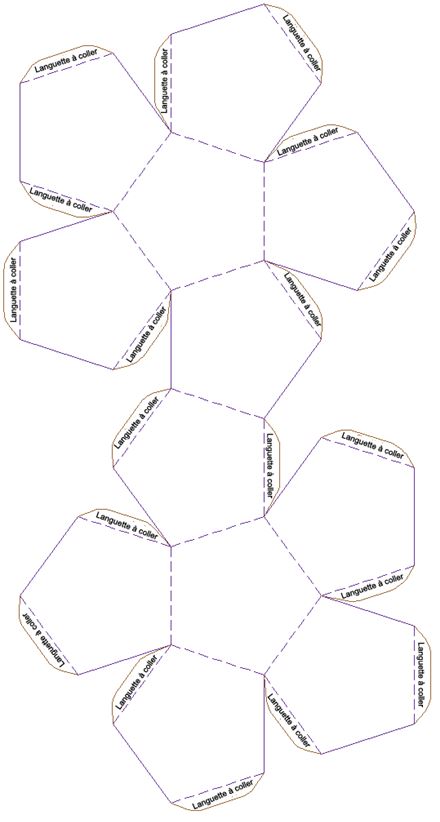
Ressource 4 : Objets en 3D
![]() Information préliminaire ou connaissance du sujet, pour l’enseignant
Information préliminaire ou connaissance du sujet, pour l’enseignant
Version en ligne
Vous trouverez des ressources utiles sur les sites web ci-dessous.
- Représenter des prismes et des cylindres de manière cavalière
http://manuel.sesamath.net/ index.php ?page=diapo&niveau=5e&atome=613
- Pyramide et cône de révolution en perspective
http://manuel.sesamath.net/ index.php ?page=diapo&niveau=4e&atome=1613
- Patrons de prismes et de cylindres
http://mathenpoche.sesamath.net/ 5eme/ pages/ geometrie/ chap6/ serie2/ index.html
- Patrons de pyramides et de cônes
http://mathenpoche.sesamath.net/ 4eme/ pages/ geometrie/ chap5/ serie2/ index.html
- La sphère
http://mathenpoche.sesamath.net/ 3eme/ pages/ geometrie/ chap3/ serie2/ index.html
- et aussi à découvrir ici :
http://pagesperso-orange.fr/ therese.eveilleau/
dans la rubrique "trucs" puis "des solides"
Version texte
Les objets en 3D comportent des surfaces (côtés), des bords et des sommets (angles).
L’exception est la sphère, qui n’a ni bords ni sommets.

Emprunté à: BBC Schools, Website
Ressource 5 : Enregistrer les résultats
![]() Destiné à l’élève
Destiné à l’élève
Forme, espace et mesures – forme
A vos formes
| Nom de la forme | Nombre de côtés | Côtés égaux ? | Côtés parallèles ? | Nombres d’angles | Angles égaux ? |
Remplissez maintenant ce tableau pour les formes 3D
| Nom de la forme | Faces | Sommets | Bords |
Source : bbc website
Section numéro 4 : Exploration de la symétrie
Question clé: Comment pouvez-vous utiliser des objets de la vie quotidienne pour développer la compréhension « abstraite » de la symétrie chez vos élèves ?
Mots clés: Lignes de symétrie ; réflexion ; rotation ; nature ; questions ouvertes ; pluridisciplinaire
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- utilisé le travail de groupe pour aider les élèves à développer leur compréhension de la symétrie, y compris les lignes de symétrie multiples et les ordres de symétrie rotationnelle ;
- développé une gamme de stratégies, y compris l’utilisation de questions ouvertes pour développer les aptitudes de réflexion dans le domaine de la symétrie ;
- travaillé dans différents domaines du programme pour développer les idées sur la symétrie.
Introduction
Si vous pliez en deux une page blanche puis l’ouvrez, chaque côté de la pliure ressemble à un reflet de l’autre. Une fois pliés, les deux côtés se chevauchent et se recouvrent parfaitement. Il s’agit d’une symétrie par réflexion. La ligne « de réflexion » ou « de pliure » qui crée ces deux reflets égaux s’appelle la ligne de symétrie.
De nombreuses formes mathématiques comportent des lignes de symétrie; de nombreux organismes vivants ont, eux aussi, une forme approximativement symétrique. Cette section vous aidera à développer votre compréhension de la symétrie et à essayer différentes stratégies pour l’enseigner.
1. Explorer en groupes la symétrie dans des objets usuels ou dans la nature
La présentation du concept de symétrie et de réflexion exige d’être soigneusement préparée. Pour faire comprendre aux élèves qu’une forme est symétrique si les deux côtés sont identiques lorsqu’on dessine une ligne de réflexion, il est préférable d’utiliser des travaux pratiques. Vous devez réfléchir à des manières d’organiser et de regrouper vos élèves pour qu’ils participent au maximum. Une manière d’introduire ce sujet est d’utiliser des dessins, des photos et des objets plats comme les feuilles. Pour trouver la ligne de symétrie, vous devez essayer :
- d’examiner une feuille de papier tenue de manière que la ligne de symétrie soit verticale - regardez d’un côté, puis de l’autre ;
- de poser une feuille de papier sur un objet, le long de la ligne de symétrie, puis de retourner la feuille pour couvrir l’autre moitié;
- de placer de petits miroirs sur la ligne de symétrie.
Lorsqu’ils examinent des objets naturels ou images, vos élèves doivent comprendre qu’ils voient uniquement une symétrie « approximative ».Par exemple, le côté gauche du visage d’une personne n’est probablement pas « exactement » le même que le côté droit. Cependant, en utilisant des exemples réels pris dans l’environnement local, comme les motifs de tissus ou la nature, vous motiverez mieux vos élèves.
Étude de cas 1 : Utilisation du travail de groupe pour explorer la symétrie
Mlle Bawa, enseignante à l'école primaire de Tchawanda, au centre du Togo, souhaite présenter à ses élèves le concept de symétrie.
Elle répartit sa classe en groupes de quatre et distribue à chaque groupe quatre formes découpées dans du papier: rectangle, carré, triangle isocèle et triangle équilatéral. Elle demande à un élève de chaque groupe de prendre le rectangle et de le plier pour que les deux côtés correspondent exactement. Le reste du groupe peut conseiller et soutenir l’élève. Elle remarque que certains groupes trouvent un seul moyen de plier le rectangle alors que d’autres en trouvent deux. Mlle Bawa demande à chaque groupe de montrer ce qu’il a fait.
Elle demande ensuite à un autre membre de chaque groupe de prendre le carré et de faire le même exercice. Les élèves de la classe concluent qu’il y a quatre manières de plier un carré. Elle explique ceci à la classe: « Ces lignes de pliure s’appellent des lignes de symétrie. Le rectangle en comporte deux, alors que le carré en a quatre. »
Sur le tableau noir, elle dessine un tableau où elle dessine les formes et demande aux élèves d’écrire le nombre de lignes de symétrie.
Elle leur demande ensuite d’expliquer la signification de « symétrique » et de « ligne de symétrie » avec des mots que tous les élèves de la classe comprennent. Ils ajoutent alors ces termes à leur dictionnaire mathématique.
Comme devoirs, elle demande aux élèves de rassembler – soit à la maison ou pendant leur trajet en rentrant de l’école – des objets qui, à leur avis, ont des lignes de symétrie. On étudiera ces objets pendant la prochaine leçon.
Activité 1 : Observation de la symétrie dans la nature
Avant la leçon, rassemblez des objets naturels qui présentent une symétrie approximative : il peut s’agir de feuilles, de fleurs ou de légumes. Vous pouvez même utiliser des animaux locaux (que vous devez toujours bien traiter) ou bien des photos d’animaux (vous pouvez demander à vos élèves de vous aider). La Ressource 1: Exemples de symétrie dans la naturecontient des photos utiles ; vous pouvez aussi en chercher dans les magazines et les journaux, ou bien apporter des tissus locaux.
Répartissez la classe en petits groupes de cinq ou six et demandez à chaque groupe d’examiner les objets ou images et d’essayer d’identifier toutes les lignes de symétrie. Présentez les réponses à toute la classe (voir la Ressource clé : Travailler en groupes dans la classe).
Demandez à vos groupes de trouver d’autres objets de la vie de tous les jours qui contiennent des lignes de symétrie. Suggérez-leur d’essayer de trouver d’autres exemples en rentrant à la maison, et demandez-leur de les noter ou d’en apporter un échantillon.
Dans la leçon suivante, demandez à chaque groupe de créer une affiche avec six objets trouvés par les élèves du groupe qui contiennent des lignes de symétrie et d’y dessiner les lignes de symétrie. Ils peuvent dessiner ou peut-être coller certains objets.
Mettez les affiches au mur pour que toute la classe puisse les voir et discutez de leurs idées après un jour ou deux pour leur rappeler le sujet.
2. Utiliser la créativité et les arts traditionnels pour explorer la symétrie (Approche interdisciplinaire)
Outre le fait d’encourager les élèves à identifier la symétrie dans le monde qui les entoure, ce sujet permet aux élèves d’exprimer leur créativité et de créer des motifs et objets symétriques. C’est une excellente opportunité pour faire du travail pluridisciplinaire avec le dessin. Ces activités peuvent être menées avec des élèves très jeunes mais sont suffisamment ouvertes pour que les élèves les plus âgés puissent être stimulés.
Étude de cas 2: Création de papillons symétriques
Mme Adoté souhaite utiliser le dessin pour aider ses élèves à explorer la symétrie. Elle a décidé de consacrer une leçon à la réalisation d’images de papillons avec ses élèves. Elle a trouvé deux photos de papillons qu’elle montre à ses élèves. Elle explique que le papillon a quatre ailes, et fait remarquer la grande variété des tailles, formes et couleurs de ces ailes, mais indique que les ailes et leurs motifs sont toujours symétriques.
Mme Adoté plie une feuille de papier et montre à la classe qu’elle peut découper la forme de l’aile d’un papillon, ouvrir la page et obtenir une paire d’ailes de papillon. Elle leur montre aussi comment réaliser des motifs de papillons en pliant du papier couvert de peinture humide. Elle invite les élèves à créer leurs propres papillons en imaginant différentes formes pour les ailes et différents motifs. Les plus jeunes élèves utilisent des taches de couleur pour leurs papillons alors que les élèves plus âgés dessinent des motifs complexes symétriques.
Lorsque les papillons sont terminés, Mme Adoté les suspend au plafond de la classe avec de la ficelle. Ses élèves sont passionnés par cette présentation et parlent beaucoup des motifs.
Activité 2: Masques symétriques
Vous devez avoir suffisamment de papier et de crayons de couleur ou de peinture pour que chaque élève puisse créer un masque coloré, plus de la ficelle ou de l’élastique pour attacher les masques et des morceaux de carton assez grands pour créer les masques.
Vous devrez sans doute passer un certain temps à rassembler ces ressources avant de pouvoir organiser l’activité, mais vos élèves pourront peut-être vous aider à rassembler des matériaux (voir la Ressource clé : Être un enseignant inventif et créatif dans des conditions difficiles).
Expliquez aux élèves qu’ils vont réaliser un masque, mais que la forme du masque et les décorations dessinées ou peintes doivent être symétriques. Suggérez-leur de faire un brouillon avant de commencer à travailler. Vous pouvez leur montrer des masques locaux. Ils peuvent peut-être rassembler des ressources et faire un brouillon pendant une leçon, et créer le masque lui-même au cours d’une ou deux leçons suivantes.
Suggérez-leur de réaliser des masques de personnes, feuilles, animaux, ailes, créatures imaginaires ou bien des masques tribaux. Vous pouvez laisser cette décision à chaque élève ou bien la prendre pour toute la classe.
Réfléchissez aux ressources qui pourraient aider les élèves à concevoir leurs masques (comme des photos ou des objets – voir la Ressource 2 : Exemples de symétrie dans les masques africains). Quelles autres activités les élèves peuvent-ils faire pour consolider leur compréhension de la symétrie ?
3. La symétrie de rotation, des exemples d’exploration pratique
Jusqu’à présent, nous avons principalement examiné une ou deux lignes de symétrie, mais certains objets ont plusieurs lignes de symétrie - un carré en a quatre : une verticale, une horizontale et deux diagonales. Le carré a également une symétrie de rotation car si nous le faisons pivoter (tourner) nous pouvons obtenir le même motif. On peut faire pivoter un carré pour obtenir le même motif quatre fois - il a une symétrie de rotation de quatre. Ceci s’appelle parfois « avoir une symétrie de rotation de l’ordre de 4 » .
La partie suivante explore plus profondément l’idée de plusieurs lignes de symétrie en utilisant des objets de la vie de tous les jours et en recherchant des motifs dans les formes. Certains de vos élèves pourront peut-être prédire le motif si vous organisez l’activité de manière à leur permettre de travailler à leur rythme et de parler de leurs idées avec les autres.
Étude de cas 3: Étudier les lignes de symétrie multiples
M. Koffi pense que ses élèves ont compris le fonctionnement d’une ligne de symétrie et souhaite les pousser un peu plus en examinant plusieurs types de symétrie. Il dessine et découpe quatre symboles religieux différents (voir la Ressource 3 : Symétrie - lignes et rotation) aussi grands que possible sur une feuille de papier format A4.
M. Koffi montre ces formes et demande si les élèves connaissent le nom de chacune. Tout d’abord, il demande à ses élèves de rechercher les lignes de symétrie. Sur la croix et la mosquée, ils trouvent facilement la ligne. Avec un peu d’encouragement, ils arrivent à voir qu’il y a de nombreuses lignes de symétrie possibles sur l’étoile de David et la roue du Dharma ; les élèves plus âgés peuvent les compter.
M. Koffi place alors une punaise au centre de la croix et montre que s’il la fait pivoter il n’y a qu’une position dans laquelle elle a le même aspect : la position de départ. Il explique que cela signifie que la croix n’a pas de symétrie de rotation. Il montre aux élèves les autres formes ; ils essaient la même rotation avec chacune d’entre elles. Ils comptent une symétrie de rotation de six pour l’étoile de David et de huit pour la roue du Dharma. Ses élèves sont avides de trouver d’autres formes dans la vie quotidienne comportant plusieurs lignes de symétrie, ce qui fait plaisir à M. Koffi.
D’autres exemples de symétrie figurent dans la Ressource 4 : Exemples de symétrie dans l’art et les tissus.
Activité clé : Explication des rotations
Il vous faut une page de formes de polygones (voir la Ressource 5 : Polygones) pour chaque petit groupe d’élèves.
Commencez par demander aux élèves d’inscrire dans leur cahier trois titres de colonnes : « côtés de polygone », « lignes de symétrie » et « symétrie de rotation ». Demandez-leur ensuite d’examiner les formes et, pour chaque polygone, de compter et d’écrire:
- le nombre de côtés de la forme.
- le nombre de lignes de symétrie qu’ils peuvent identifier.
- le nombre d’ordres de symétrie de rotation qu’ils peuvent identifier.
Après avoir travaillé sur quelques formes, certains élèves commenceront à identifier une structure et pourront remplir leur tableau sans compter ; d’autres ne verront pas la structure. Lorsque cela se produit, demandez aux élèves qui ont identifié une structure d’expliquer aux autres son fonctionnement.
Utilisez des questions du type: « Combien de lignes de symétrie aurait un polygone de x côtés ? Et combien d’ordres de symétrie de rotation ? » (x peut être n’importe quel nombre entier.)
Demandez à chaque groupe de remplir le tableau que vous avez dessiné sur une feuille de papier journal et affichez leurs tableaux dans la classe (voir la Ressource 6 : Enregistrer la symétrie).
Ressource 1 : Exemples de symétrie dans la nature
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
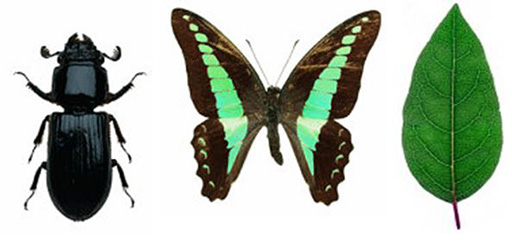
Source: Getty Images, Site web
Ressource 2 : Exemples de symétrie dans les masques africains
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
 |  |
 |  |
Source: Tribal Hunter: Unique Tribal Arts, Website; Pitt Rivers Museum, Website; Wills Henry Auctions, Website;Building Virtual Learning Communities:Spelman Bush-Hewlett Grant, Website
Ressource 3 : Symétrie - lignes et rotation
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
| Symbole religieux | Lignes de symétrie | Ordre de symétrie de rotation |
 | 12 | 6 |
 | 1 | 0 |
 | 1 | 0 |
 | 16 | 8 |
Ressource 4 : Exemples de symétrie dans l’art et les tissus
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
 |  |
 |  |
Source: Islamic Architecture, Website; Virignia Commonwealth University Blog, Website
Exemples de symétrie dans les motifs de tissus nigérians

Le drapeau nigérian est également symétrique. Vos élèves peuvent-ils identifier d’autres drapeaux symétriques ?
Le drapeau du Rwanda est-il symétrique ? Vos élèves peuvent-ils expliquer cette réponse ?

Certaines fenêtres des maisons au Rwanda ont des formes symétriques. Pouvez-vous trouver d’autres objets dans le quartier qui sont symétriques ?
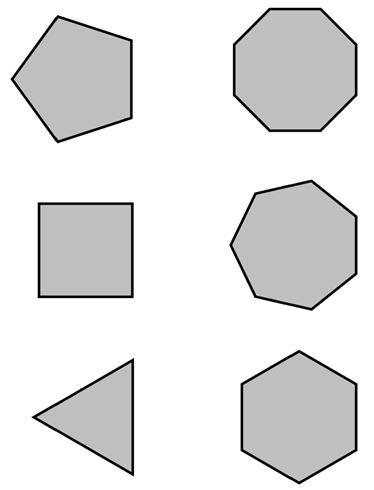
Ressource 5 : Polygones
![]() Utilisation par les élèves
Utilisation par les élèves
Vous devrez utiliser les polygones en 2D suivants:
- Pentagone
- Octogone
- Carré
- Heptagone
- Triangle
- Hexagone
Ressource 6 : Enregistrer la symétrie
![]() Utilisation par les élèves
Utilisation par les élèves
| Objet | Lignes de symétrie | Ordre de symétrie de rotation |
Section numéro 5 : Enseignement des transformations
Question clé: Comment pouvez-vous développer les aptitudes de modélisation mentale en géométrie ?
Mots clés: Congruence ; translation ; réflexion ; transformation ; multigrade ; différenciation ; pratique
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- présenté aux élèves la transformation, la congruence, la translation et la réflexion ;
- utilisé des formes découpées pour développer la transformation mentale des formes géométriques ;
- examiné les problèmes associés à la différenciation de ce travail pour les élèves plus âgés et plus jeunes et essayé différentes méthodes.
Introduction
Dans notre vie quotidienne, nous voyons de nombreux exemples de formes qui ont été modifiées (changées) ou transformées.
Cette section vous aidera à développer vos propres connaissances de la géométrie et de la transformation ainsi que vos aptitudes pour développer la compréhension de vos élèves.
L’objectif de la plupart des ressources de cette section est donc de renforcer vos connaissances en tant qu’enseignant de mathématiques.
1. Travailler collaborativement pour préparer des travaux pratiques sur les formes congruentes
En géométrie, le terme « transformation » signifie la modification d’une propriété géométrique d’une forme (rotation, déplacement de sa position sur la page) tout en conservant d’autres propriétés de la forme (nous disons que les formes sont « congruentes »).
Une excellente manière pour les élèves de modéliser les transformations est d’utiliser des objets physiques ou d’examiner des objets de la vie quotidienne et leur transformation, par exemple dans les motifs des tissus. Pendant que les élèves travaillent, encouragez-les à vous parler et à parler ensemble de ce qu’ils font. Le fait de parler de la manière dont ils essaient de manipuler les objets améliorera leur compréhension de la géométrie ainsi que celle de la langue qui y est associée.
Étude de cas 1 : Préparer une leçon de géométrie avec un(e) collègue
Mme Wolou, enseignante dans une école primaire de Tchamba, au Togo, parle de son expérience de l’enseignement de la géométrie à ses élèves avec une collègue ayant plus d’ancienneté, Mme Atayi. Elle se plaint que les élèves n’aiment pas cette discipline scolaire. Ses élèves se plaignent que la géométrie est très abstraite et exige beaucoup d’imagination. En plus, ils trouvent qu’elle a peu ou pas de rapport avec la vie de tous les jours. Mme Wolou a donc peu d’enthousiasme quand il s’agit d’enseigner cette discipline.
Mme Atayi reconnaît qu’elle a eu des expériences similaires mais encourage sa collègue à essayer d’utiliser une méthode d’enquête pratique et à inviter ses élèves à parler de ce qu’ils font.
Ensemble, les enseignantes préparent une leçon durant laquelle les élèves feront des activités détaillées en utilisant des échantillons de tissus à motifs contenant des translations et variations de formes (voir la Ressource 1 : Quelques motifs de tissus nigérians). Ceci peut permettre aux élèves de découvrir eux-mêmes les concepts à apprendre.
Mme Atayi et Mme Wolou font alors chacune cette leçon dans leur classe et se réunissent ensuite pour parler des résultats. Mme Wolou est surprise de constater le niveau de réflexion de ses élèves et leur désir de parler de ce qu’ils faisaient. Mme Atayi conclut elle aussi que le fait d’autoriser les élèves à parler de leur travail les a passionnés et leur a donné confiance en leurs aptitudes en mathématiques.
Activité 1 : Étudier les formes congruentes
Pour cette activité, il vous faudra un morceau de carton, un crayon et une règle pour chaque petit groupe d’élèves (2 ou plus), et plusieurs paires de ciseaux.
- Demandez à vos élèves de dessiner sur leur morceau de carton trois formes différentes dont les côtés sont droits, puis de découper leurs formes. Ils doivent numéroter chacune de leurs formes en carton 1, 2 ou 3.
- Ensuite, sur une feuille séparée, demandez à vos élèves de dessiner le contour de chaque forme puis de déplacer les formes comme ils veulent sans chevaucher ce qu’ils ont déjà dessiné, puis de dessiner à nouveau le contour des formes. Demandez-leur de continuer de cette manière jusqu’à ce que la page soit pleine de formes, puis d’ajouter un identifiant alphabétique à l’intérieur de chaque contour (a, b, c…). Le travail terminé doit ressembler à la Ressource 2 : Exemples de formes congruentes.)
- Demandez aux élèves d’échanger leur travail avec celui d’un autre groupe. Peuvent-ils identifier les contours tracés avec la même forme ? (Les enfants plus jeunes devront peut-être utiliser les formes en carton pour s’aider.) Demandez-leur d’écrire leurs réponses, par exemple forme 1, contours a, b, d, g.
- En utilisant la forme découpée, peuvent-ils vous montrer ce qui doit se passer lorsqu’on va d’un contour à un autre ? Peuvent-ils le décrire ?
- Ceux qui finissent les premiers peuvent colorier leur travail, en utilisant la même couleur pour les contours provenant de la même forme. Vous pouvez afficher ces feuilles sur les murs de la classe, avec le titre « Formes congruentes ».
2. Des activités différenciées pédagogiquement pour enseigner la translation
L’une des transformations les plus simples est la translation. Pour translater une forme, nous déplaçons simplement sa position sur la page, vers le haut, vers le bas, vers la gauche ou vers la droite, sans aucun autre changement (voir la Ressource 3 : Translation).
Comme la translation d’une forme est une procédure simple, les élèves les plus jeunes peuvent comprendre cette idée, surtout s’ils ont des formes physiques qu’ils peuvent manipuler. Pour les élèves plus âgés, cette activité peut devenir plus difficile en utilisant des coordonnées (x,y) et des calculs au lieu de simplement manipuler des formes physiques.
L’Étude de cas 2 et l’Activité 2 examinent la translation et la manière de différencier les tâches en fonction de l’âge et du stade.
Étude de cas 2: Développement de la compréhension de la translation
Mme Kpoffon a une classe à niveaux multiples, qui contient un groupe de quatre enfants plus âgés obtenant de bons résultats en mathématiques. Elle trouve que leur travail actuel ne les stimule pas suffisamment et saisit une occasion de leur présenter un véritable défi. (Pour avoir plus d’informations sur l’enseignement aux classes à niveaux multiples, voir la Ressource clé : Travailler avec des classes à effectifs lourds ou à niveaux multiples.)
Mme Kpoffon a déjà présenté le concept de coordonnées (x,y) à toute la classe. Un jour, pendant que la plupart de la classe travaille sur une activité de translation de triangles en utilisant des formes découpées, Mme Kpoffon donne un soutien supplémentaire à ces quatre élèves (voir la Ressource 4 : Translater et refléter les triangles)
Après avoir dessiné un triangle comportant des axes (x,y) identifiés sur du papier quadrillé, elle demande aux élèves quelles sont les coordonnées des trois angles (sommets) - ils trouvent la réponse facilement et l’écrivent. Ensuite, elle leur demande « Que se passerait-il si je déplaçais cette forme de six espaces vers la droite ? Quelles seraient les nouvelles coordonnées (x,y) ? » Lorsqu’ils répondent correctement, elle continue : « Et si je déplaçais la forme de 3 espaces vers le bas ? » Mme Kpoffon continue ainsi jusqu’à ce qu’elle estime que les élèves comprennent clairement ce qui se passe.
Elle leur dit ensuite : « Maintenant, chacun d’entre vous doit poser un problème aux autres - donnez les coordonnées d’un triangle et une translation à appliquer au triangle. Écrivez les informations, puis dessinez le triangle qu’on vous a décrit, calculez les coordonnées translatées et dessinez la nouvelle position. Si vous le faites correctement, vous pouvez ensuite essayer des formes autres que les triangles pour vous tester les uns les autres. »
Les élèves apprécient le respect de leur enseignante et la possibilité de travailler plus librement et de se poser mutuellement des défis mathématiques.
Activité 2: Étudier les translations en pratique
Vérifiez que les élèves comprennent comment donner les coordonnées (x,y) en faisant une leçon à toute la classe. Pour différencier la tâche pour les élèves plus âgés ou plus jeunes, consultez les notes sur la différenciation dans la Ressource 4 : Translater et refléter les triangles.
Demandez aux élèves de dessiner et de découper un triangle, un carré et un rectangle dans une feuille de papier quadrillé: insistez sur le fait que chaque angle (ou sommet) de leurs formes doit se trouver à l’une des « croix » de leur papier quadrillé. Dessinez un exemple au tableau.
Aucun côté ne doit faire plus de 10 carrés de long.
Sur une seconde feuille de papier quadrillé, demandez aux élèves de dessiner et d’identifier des axes (x,y) de 20 carrés de longueur au minimum (voir la Ressource 4).
En posant l’une de leurs formes découpées sur le papier pour que ses angles se trouvent sur les « croix » du papier quadrillé, ils doivent marquer les sommets (a, b, c et d selon les cas) puis dessiner la forme et écrire les coordonnées de chaque sommet.
Demandez-leur de déplacer leur forme à une nouvelle position (sans la faire pivoter) et répétez ce processus.
Demandez ceci à vos élèves. « Que deviennent les coordonnées x entre les deux positions ? La même chose se produit-elle pour chaque coordonnée ? Que deviennent les coordonnées y ? »
Quelles parties de cette activité ont posé des problèmes à vos élèves ? Comment les soutiendrez-vous la prochaine fois ?
3. Des idées pratiques pour aider les élèves à comprendre la réflexion (mathématique)
La translation est relativement simple car elle touche les coordonnées de tous les sommets de la même manière (par exemple, toutes les coordonnées x augmentent ou diminuent de la même manière).
La réflexion est plus complexe sur le plan mathématique car vous devez traiter chaque coordonnée séparément et en relation avec un autre élément - la position de la ligne de réflexion. La réflexion exige donc que les élèves gardent à l’esprit plusieurs idées différentes à la fois (voir la Ressource 4). Réfléchissez aux exemples familiers de réflexion que vous pourriez utiliser pour aider vos élèves - peut-être un travail fait sur la symétrie ou les motifs et dessins dans les œuvres d’art, en utilisant les idées traditionnelles locales. Réfléchissez à la manière dont les élèves pourraient utiliser des formes découpées pendant qu’ils développent la capacité à manipuler ces formes mentalement.
Cette partie vous suggère également de continuer à encourager vos élèves à parler de leur réflexion - il s’agit d’un aspect très important pour révéler leur compréhension des mathématiques.
Étude de cas 3: Utiliser le travail en groupe pour faciliter la compréhension des réflexions
Mme Dao Dao, une enseignante expérimentée dans une école primaire de Sanda au Togo a enseigné les bases de la réflexion à sa classe. Elle décide maintenant d’aider ses élèves à parler de leur activité et de leurs conclusions.
Sachant qu’une discussion ne consiste pas simplement à répondre à de courtes questions fermées, elle décide de créer une structure pour faciliter la discussion parmi ses élèves. Elle les répartit par groupes de deux. Elle leur demande d’examiner le travail de leur partenaire et de faire trois observations sur la réflexion, qu’ils devront ensuite présenter. Pour chaque observation, les deux élèves du groupe doivent trouver une description ou explication aussi claire que possible, dont ils sont tous deux satisfaits. Lorsque les deux élèves du groupe sont d’accord sur trois observations claires, ils doivent lever la main.
Mme Dao Dao forme alors des équipes de quatre en regroupant deux groupes deux et demande à chaque groupe de deux d’expliquer ses observations à l’autre groupe de l’équipe. Elle demande enfin aux équipes de quatre de décider quelles sont les trois observations les meilleures ou les plus intéressantes pour les présenter à la classe.
Elle s’aperçoit qu’elle pourrait utiliser cette manière de travailler pour des leçons autres que les mathématiques. Pour découvrir ce que savent vos élèves et ce qu’ils peuvent faire, consultez la Ressource clé : Évaluer l’apprentissage.
Activité clé : Comprendre les réflexions
Vos élèves peuvent réutiliser les formes découpées dans le papier quadrillé dans l’Activité 2, ou bien en créer d’autres si nécessaire.
Sur une seconde feuille de papier quadrillé, demandez aux élèves de dessiner et d’identifier des axes (x,y) de 20 carrés de longueur au minimum (voir la Ressource 4).
En posant l’une de leurs formes découpées sur le papier pour que ses angles se trouvent sur les « croix » du papier quadrillé, ils doivent marquer les sommets (a, b, c et d selon les cas) puis dessiner la forme et écrire les coordonnées de chaque sommet (angle).
Demandez aux élèves de dessiner une ligne de réflexion verticale ou horizontale sur leur quadrillage. Ils doivent alors dessiner le reflet de la forme de l’autre côté de la ligne de réflexion (rappelez aux élèves qu’ils peuvent utiliser la forme découpée s’ils trouvent cela utile) et écrire les coordonnées de la réflexion.
Pour rendre les choses plus difficiles, demandez à vos élèves de calculer les coordonnées de la réflexion sans utiliser la forme découpée. Demandez-leur d’expliquer comment ils ont réussi à faire ça. Faites des exercices en utilisant un nombre de formes différentes pour que les élèves prennent confiance en eux.
Avez-vous réussi à bien introduire et expliquer ce travail ? Comment le savez-vous ?
Ressource 1 : Quelques motifs de tissus nigérians
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
 |  |

Source: Adire African Textiles, Website
Ressource 2 : Exemples de formes congruentes
![]() Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Ressource de l’enseignant pour la préparation ou l’adaptation, à utiliser avec les élèves
Si deux formes sont congruentes, leur forme et leur taille est identique.
Question: Parmi les formes suivantes, lesquelles sont congruentes ?
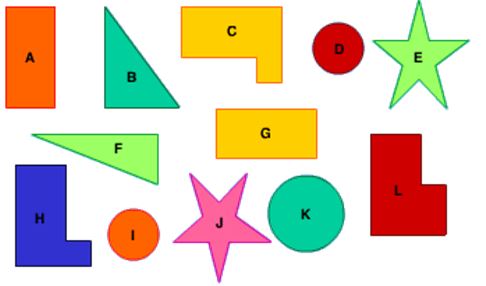
Réponses
- A et G
- D et I
- E et J
- C et H
N’oubliez pas que les formes peuvent être congruentes même si l’une d’entre elles a été pivotée (comme dans A et G) ou reflétée (comme dans C et H).
Source: BBC Schools Website
Ressource 3 : Translation
![]() Informations sur le contexte/la connaissance du sujet, pour l'enseignant
Informations sur le contexte/la connaissance du sujet, pour l'enseignant
Version texte
Quand nous translatons une forme, nous la déplaçons vers le haut ou le bas, ou vers la droite ou la gauche, mais nous ne changeons rien d’autre à son apparence.
Lorsque nous translatons une forme, chacun des sommets (angles) doit être déplacé exactement de la même manière.
Parmi les formes suivantes, lesquelles sont des translations du triangle A ?
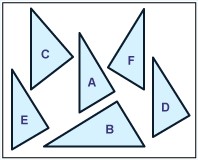
Réponses: D et E sont des translations du triangle A.
Emprunté à: BBC Schools, Website
Ressource 4 : Translater et refléter les triangles
![]() Information préliminaire ou connaissance du sujet, pour l'enseignant
Information préliminaire ou connaissance du sujet, pour l'enseignant
Translation du triangle abc au triangle a1b1c1

Les coordonnées (x,y) donnent toujours la valeur «x» (axe horizontal) avant la valeur «y» (axe vertical).
Donc, dans l’illustration, les coordonnées (x,y) des points a,b,c sont:
a = 4, 8
b = 4, 2
c = 2, 2
La translation à a1b1c1 augmente la valeur de x de 12 et celle de y de 9. Donc:
a1 = 16, 17
b1 = 16, 11
c1 = 14, 11
Différenciation
Cette activité peut être simplifiée en déplaçant une forme découpée sur le quadrillage, en en dessinant le contour et en enregistrant les nouvelles coordonnées.
Cette activité peut être rendue plus difficile en donnant les coordonnées d’une forme et en demandant aux élèves de dessiner la forme. Expliquez alors comment une translation modifie les valeurs de (x,y) et demandez-leur de calculer les nouvelles coordonnées et de redessiner la nouvelle position de la forme.
Réflexion du triangle abc au triangle a1b1c1
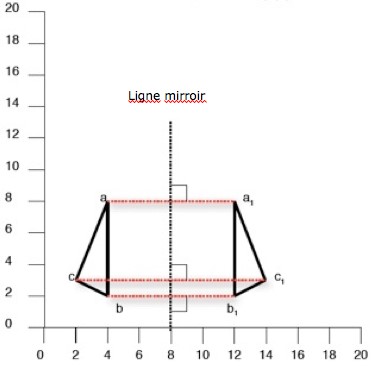
Donc, dans l’illustration, les coordonnées x-y d’abc sont :
a = 4, 8
b = 4, 2
c = 2, 3
La réflexion d’abc dans une « ligne de réflexion » verticale (x=8) donne une image (a1b1c1) avec de nouvelles coordonnées :
a1 = 12, 8
b1 = 12, 2
c1 = 14, 3
N.B.
L’objet et son image sont toujours à la même distance perpendiculaire (la distance mesurée à angle droit) de la ligne de réflexion, par exemple si « a » se trouve à 4 carrés de la ligne de réflexion, a1 doit aussi se trouver à 4 carrés de la ligne de réflexion.
Comparez les coordonnées x-y d’abc et de a1b1c1 et remarquez qu’une ligne de réflexion verticale ne modifie pas les coordonnées y.
De même, une ligne de réflexion horizontale ne modifie pas les coordonnées x.