Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated lundi 9 mars 2026, 17:41
Module 1 : Étude du nombre et de la structure
Section numéro 1 : Apprentissage par le jeu
Question clé: Comment les jeux peuvent-ils aider les élèves à apprendre les bases de la numération ?
Mots clés: jeux ; travail en groupe ; enquête ; compétences en numération
Résultats de l’apprentissage
À la fin de cette section, vous aurez:
- développé des manières d’utiliser les jeux pour éveiller l’intérêt des élèves pour les mathématiques ;
- utilisé toute une gamme de jeux pour améliorer la compréhension mathématique et les compétences en numération.
Introduction
L’utilisation de jeux en classe peut faciliter la compréhension et les aptitudes mathématiques de vos élèves. Il peut s’agir de jeux arithmétiques mentaux auxquels toute la classe participe ou bien de jeux de société plus complexes.
Cette section explore le rôle des jeux comme moyen coopératif d’éveiller l’intérêt et la réflexion sur les nombres.
En utilisant des jeux culturels locaux, vous mettez mieux les mathématiques en relation avec la vie quotidienne des élèves.
1. Utilisation de jeux pour développer le calcul mental
L’utilisation de jeux pour motiver tous les élèves, y compris ceux qui sont parfois réticents durant les leçons de mathématiques, peut avoir des effets très positifs.
Les enfants peuvent s’exercer au calcul mental et à d’autres aptitudes tout en jouant.
Vous devez toujours essayer les jeux vous-même avant de les présenter aux élèves. Ceci vous permettra de les comprendre et de pouvoir les expliquer clairement ; cette pratique vous aidera aussi à identifier la réflexion mathématique nécessaire pour chaque jeu. Vous pouvez créer les jeux vous-même ou avec votre classe ; ils peuvent être utilisés de nombreuses fois.
Étude de cas 1 vous montre comment un enseignant a utilisé des jeux pour améliorer les compétences de ses élèves en calcul mental. Activité 1 vous présente un jeu de mémoire simple.
Étude de cas 1 : Utilisation des jeux de nombres pour faciliter le calcul mental
Mlle Ama, enseignante au cours préparatoire deuxième année (seconde année de primaire) au Togo, s’aperçoit que ses élèves aiment jouer à des jeux de nombres pendant la récréation. Les garçons font rouler des ballons dans des arceaux numérotés sur une table et les filles lancent des sacs remplis de cailloux sur une cible. Dans chaque jeu, le gagnant est le premier élève à obtenir 20 points ; Mlle Ama remarque que certains de ses élèves réussissent mieux que d’autres à additionner les scores.
Elle décide d’introduire des jeux similaires dans son enseignement pour voir si tous ses élèves peuvent faire des additions. Elle utilise le même jeu chaque jour avec un groupe à la fois, pendant une semaine. Le reste de la classe fait des exercices et elle partage son temps entre le soutien apporté au groupe participant au jeu et le reste de la classe (voir la Ressource clé : Travailler en groupes dans la classe).
Elle s’aperçoit qu’un petit groupe d’élèves a plus de mal à faire des additions mentales. Elle donne donc à ces élèves des opportunités de jeu supplémentaires et organise d’autres leçons de calcul mental pour eux.
Mlle Ama s’aperçoit également que ses élèves sont plus empressés de venir à l’école et décide d’utiliser plus de jeux dans sa classe dans l’avenir.
Activité 1 : Jeu de mise en correspondance des questions et réponses
Vous devez essayer les jeux vous-même initialement pour bien connaître les règles et pouvoir les expliquer clairement à votre classe.
Ce jeu permet à vos élèves de s’entraîner à l’association simple de nombres et d’utiliser leurs aptitudes d’observation et de mémorisation. Si vous avez des élèves plus grands, vous pouvez adapter ce jeu en utilisant d’autres nombres et additions. Voir la Ressource 1 : jeux d’association de nombres pour avoir les règles du jeu et connaître des manières d’adapter le jeu.
Vous devez réaliser plusieurs copies du jeu ou bien demander aux élèves de vous aider en réalisant leur propre copie.
Répartissez vos élèves en groupes de cinq ou six et donnez un jeu à chaque groupe.
Encouragez les groupes à dialoguer à propos du jeu et des règles.
Chaque groupe choisit un chef qui vérifie que les règles du jeu sont respectées.
Pendant que les élèves jouent, faites le tour de la classe pour identifier ceux qui ont des problèmes – cela vous permet de réfléchir à des manières de les aider plus tard.
Demandez-vous : Quelles compétences de numération les élèves utilisent-ils quand ils jouent à ces jeux ?
Voici des questions que vous pourriez vous poser ou dont vous pourriez discuter avec un(e) collègue :
- Les élèves ont-ils aimé les jeux ? Comment savez-vous qu’ils les ont aimés ?
- Tous les élèves ont-ils participé ? Dans la négative, comment pourriez-vous faire en sorte que tout le monde participe ?
- Avez-vous eu l’impression de contrôler toute la classe ?
- Comment pourriez-vous améliorer cette leçon ? Des groupes plus petits seraient-ils préférables ?
- Avez-vous donné assez de temps aux élèves pour les tâches ?
2. Identifier les mathématiques pratiquées dans le jeu – Jouer en groupes
Les jeux peuvent être joués par de petits groupes ou par la classe entière. Lorsque toute la classe participe, il faut une certaine préparation et des ressources adéquates. En autorisant les jeux en dehors des horaires de classe, vous encouragerez l’assimilation et la consolidation des idées. La création d’un club de jeux dans votre école peut aussi encourager plus d’élèves à jouer.
Pensez aussi à évaluer le niveau de difficulté d’un jeu afin de choisir un jeu adapté à vos élèves. Étude de cas 2 vous montre une enseignante organisant un jeu avec sa classe et Activité 2 vous montre comment organiser plusieurs jeux à la fois.
Étude de cas 2: Jouer au loto pour faciliter l’identification des nombres
Hodalo joue au loto avec sa classe du cours préparatoire deuxième année(seconde année de primaire) car elle pense que c’est un jeu formidable pour aider les élèves à identifier les nombres à deux chiffres.
Elle organise d’abord une partie avec toute la classe. Elle donne à chaque élève une grille et des boutons. Un élève tire des cartes numérotées de 1 à 50 dans une boîte et lit le contenu à la classe. Quand un élève trouve le nombre lu sur sa grille, il met un bouton dessus. Le premier élève dont les boutons couvrent une ligne, une colonne ou une diagonale sans erreurs est le gagnant. Pendant que les élèves jouent, Hodalo se déplace dans la classe pour les aider. Le fait d’avoir une ligne, une colonne ou une diagonale complète prouve la capacité à identifier correctement les nombres à deux chiffres.
Elle divise ensuite la classe en groupes de huit élèves qui jouent à leur rythme, en prenant le rôle de tirage au sort des numéros chacun à leur tour.
Hodalo autorise aussi les élèves à jouer au loto pendant la récréation. Elle est surprise de voir qu’ils sont nombreux à y jouer, surtout par temps de pluie. Elle remarque aussi que les élèves ont beaucoup plus d’assurance dans les leçons de mathématiques. Elle élargit ensuite le jeu en plaçant plus de grilles dans le jeu contenant les nombres 51 à 99 pour ses élèves plus aptes.
Voir la Ressource 2 : Jeux pour pratiquer les compétences en numération pour avoir les règles du jeu de loto et d’autres jeux simples.
Activité 2: Identifier les mathématiques des jeux
Dans cette activité, demandez à vos élèves de jouer l’un de cinq jeux et d’identifier les mathématiques qu’ils pensent être en train d’apprendre (voir la Ressource 2). Vous devrez peut-être les aider à identifier les mathématiques.
- Répartissez vos élèves par groupes de quatre ou cinq.
- Donnez l’un des cinq jeux de nombres à chaque groupe.
- Demandez à chaque groupe de parler du jeu en vérifiant que les élèves comprennent les règles avant de jouer.
Après avoir joué à chaque jeu pendant une durée déterminée, demandez aux groupes de vous donner la liste des mathématiques qu’ils pensent avoir utilisées en utilisant le tableau de la Ressource 3 : Tableau pour enregistrer les compétences en numération.
Vous pouvez alors demander aux groupes d’essayer l’un des autres jeux. Si vous avez le temps, vous pouvez continuer jusqu’à ce que chaque groupe ait essayé les cinq jeux (cette rotation de différentes activités s’appelle parfois un « cirque » - l’utilisation d’une technique de cirque permet d’utiliser un équipement (dans ce cas un jeu spécifique) avec toute la classe.
Affichez tous les résultats pour pouvoir en discuter.
Vous devrez peut-être les laisser jouer pendant plus d’une leçon ou bien pendant les récréations.
3. Utiliser des jeux culturels traditionnels
Les jeux culturels sont une autre manière de motiver les élèves. Cela les aide à voir que les mathématiques sont une activité populaire, universelle et historique. Il existe un jeu très populaire (Ressource 4 : le jeu culturel africain) pratiqué partout en Afrique et qui porte différents noms.
Il existe de nombreuses versions de ce jeu. Il fait appel à des compétences mathématiques importantes et peut être joué par des élèves d’âges différents.
Il est important qu’un enseignant comprenne comment les jeux peuvent être adaptés aux élèves d’âges différents. Par exemple, sous sa forme la plus simple, ce jeu convient aux élèves plus jeunes car il encourage l’action de compter et la compréhension de la correspondance un à un. On peut étendre le jeu pour inclure l’addition et la soustraction. Si vous avez des classes à niveaux multiples, consultez la ressource clé : Travailler avec des classes à effectifs lourds ou à niveaux multiples
Étude de cas 3: Identifier les aptitudes de numération avec un jeu culturel
M. Zakari parle à sa classe d’un jeu (voir la Ressource 3) auquel il jouait quand il était enfant. Il explique aux élèves qu’ils y joueront pendant leur prochaine leçon de mathématiques.
Il montre le tableau à la classe et fait la démonstration du jeu en demandant à deux élèves de jouer pendant qu’il explique les règles. Pendant que les élèves regardent, il les encourage à poser des questions.
Il distribue ensuite des supports permettant aux élèves de jouer deux par deux (quatre élèves par jeu) de manière à ce qu’ils puissent parler des règles avec leur partenaire. A la fin de la partie, il leur demande d’identifier les aptitudes de numération nécessaires pour le jeu.
Enfin, il donne aux élèves l’autorisation d’emporter les jeux chez eux pour y jouer avec quelqu’un jusqu’à la fin de la semaine.
A la fin de la semaine, M. Zakari demande à ses élèves ce que leur famille pense du jeu. Beaucoup disent que leurs parents et grands-parents ont joué à ce jeu quand ils étaient enfants.
Activité clé : utiliser un jeu de nombres culturel
Avant de commencer, vérifiez que vous connaissez bien les règles du jeu (voir la Ressource 3). Rassemblez un nombre suffisant de supports et 48 cailloux pour chaque groupe.
Divisez la classe en groupes de quatre élèves et donnez à chaque groupe un support et 48 cailloux.
Demandez à chaque groupe de choisir deux volontaires qui vont jouer.
Les deux autres membres du groupe aideront les volontaires à jouer.
Pendant que le jeu progresse, déplacez-vous dans la classe pour aider les élèves qui en ont besoin. Ecoutez ce que disent les élèves et notez les termes mathématiques qu’ils emploient.
Discutez avec les élèves de ce que vous venez d’entendre. Quelles aptitudes mathématiques utilisaient-ils pendant le jeu ?
Ressource 1: Jeux d’associations de nombres
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Voici les instructions pour le jeu de mise en correspondance des questions et réponses. Vous trouverez ci-dessous des exemples de questions et réponses. Vous pouvez les recopier ou demander à vos élèves de dessiner eux-mêmes les tableaux.
Découpez chaque case séparément.
2 à 6 joueurs peuvent participer à la fois.
Posez toutes les cartes sur la table, face cachée. Les réponses et les questions doivent être dans deux piles séparées pour aider les joueurs.
Décider qui joue en premier. Chaque joueur attend son tour pour retourner deux cartes – une dans la pile des additions et une dans la pile des réponses. Si la réponse correspond à l’addition, le joueur déclare la première « correspondance ». S’il obtient une correspondance, il peut retourner deux nouvelles cartes. Dans le cas contraire, c’est le tour du joueur suivant. Continuer jusqu’à ce que toutes les additions aient trouvé une réponse. Le gagnant est le joueur qui obtient le plus de correspondances.
On peut rendre le jeu plus difficile pour des élèves plus grands en utilisant des additions plus complexes, des soustractions, des multiplications et des divisions. Il faudra adapter les « réponses » en conséquence.
Exemples de questions portant sur des additions
| 1+0= | 0+2= | 1+1= | 2+0= |
| 1+2= | 2+1= | 0+4= | 1+3= |
| 3+1= | 2+2= | 0+5= | 4+1= |
| 1+4= | 2+3= | 3+2= | 0+6= |
| 1+5= | 5+1= | 2+4= | 4+2= |
| 3+3= | 0+7= | 1+6= | 2+5= |
| 5+2= | 3+4= | 4+3= | 8+0= |
| 1+7= | 2+6= | 6+2= | 3+5= |
| 4+4= | 0+9= | 8+1= | 2+7= |
| 3+6= | 4+6= | 7+3= | 9+1= |
Exemples de réponses
| 1 | 2 | 2 | 2 |
| 3 | 3 | 4 | 4 |
| 4 | 4 | 5 | 5 |
| 5 | 5 | 5 | 6 |
| 6 | 6 | 6 | 6 |
| 6 | 7 | 7 | 7 |
| 7 | 7 | 7 | 8 |
| 8 | 8 | 8 | 8 |
| 8 | 9 | 9 | 9 |
| 9 | 10 | 10 | 10 |
Ressource 2: Jeux utilisant des aptitudes en numération
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
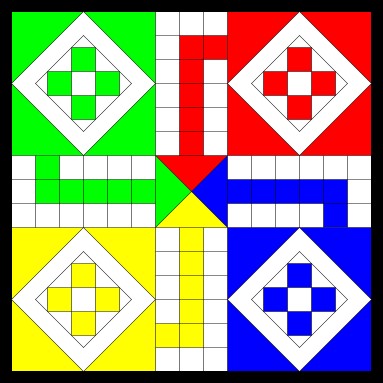
Ludo ou « Petits chevaux »
Un jeu de société simple pour enfants, destiné à deux à quatre joueurs, dans lequel les participants déplacent leurs quatre pions sur un parcours selon le nombre indiqué par les dés.

Un jeu de Ludo typique
Source: http://www.mastersgames.com/ images/ board/ ludo-colour-1.jpg
Les participants jettent les dés et font avancer leurs pions chacun à leur tour. Lorsqu’un joueur obtient 6, il peut commencer à déplacer un autre pion. Lorsque le pion d’un joueur atterrit sur une case déjà occupée par le pion d’un autre joueur, ce dernier doit retirer son pion du jeu et attendre d’avoir obtenu 6 pour lui faire reprendre le départ. Le gagnant est le premier joueur qui parvient à amener ses quatre pions au centre du jeu, sur la zone correspondant à sa couleur.
Jeu de l’oie
Les participants jettent les dés et font avancer leurs pions chacun à leur tour. Ils suivent les consignes indiquées dans la case sur laquelle leur pion atterrit: ils passent un tour, avancent ou reculent de plusieurs cases. S’il n’y a aucune consigne dans la case, le pion reste dans cette case. Le gagnant est celui qui arrive exactement à la case finale: il doit faire le nombre de cases exact pour arriver à la case finale.

Source: http://lillibulle.typepad.com/boutique/2010/11/le-jeu-de-l-oie-londji.html
Loto
Il s’agit d’un jeu de hasard dans lequel des nombres sélectionnés au hasard sont dessinés sur un tableau de loto qui contient aussi des cases vides. En voici un exemple :
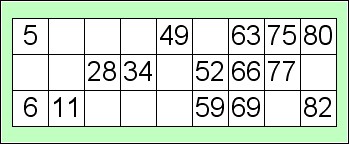
Une personne écrit les nombres de 1 à 100 généralement sur de petites boules (mais vous pouvez utiliser des cartes). Cette personne les sélectionne alors une par une au hasard, sans les regarder, et annonce le nombre. Quand un joueur retrouve ce nombre sur son tableau, il le recouvre d’un pion ou le raye. La personne qui fait le tirage au sort doit conserver séparément les nombres déjà appelés car elle en aura besoin plus tard pour la vérification. Elle continue à tirer les nombres au sort et à les annoncer jusqu’à ce qu’une personne ait recouvert tous les nombres de son tableau et s’écrie « LOTO ! ». La personne qui fait le tirage au sort doit alors vérifier que le tableau est bien correct et déclare alors cette personne gagnante.
Un jeu de cartes en boucle
Les « jeux de cartes en boucle » exigent que les élèves restent constamment attentifs car ils participent tous et ne savent pas quand leur carte va sortir.
Règles du jeu
Chaque carte porte un nombre comme 12 (ou tout autre nombre) et une question. La question peut simplement concerner l’addition ou la multiplication de nombres ou bien peut mettre en jeu les quatre règles des nombres, en fonction des aptitudes que vous souhaitez faire pratiquer aux élèves. Vous pouvez donc créer plusieurs jeux de ces cartes - certains faciles et d’autres plus difficiles – pour les utiliser à différents moments. Par exemple, certaines cartes pourraient aider les élèves qui ont des problèmes spécifiques avec les grands nombres. Les exemples dans l’illustration ci-dessous concernent la division et la multiplication par deux.
Il vous faut suffisamment de cartes pour que chaque élève en ait une. Vous pouvez aussi créer des cartes sur le thème de l’argent, des distances etc.
Pour jouer, les élèves peuvent rester assis sur leur banc ou bien vous pouvez les mettre en cercle. Donnez une carte à chaque élève. Choisissez un élève qui va commencer en lisant sa question. L’élève qui a la réponse correcte se lève et lit la réponse. S’il a bien la réponse correcte, il lit sa question. L’enfant qui a la bonne réponse à cette nouvelle question se lève et lit sa question – le jeu continue jusqu’à ce que tous les élèves soient debout (ou assis s’ils commencent le jeu debout).
Ne distribuez pas plusieurs cartes portant le même nombre car cela embrouillerait les élèves. Vous pouvez utiliser ce jeu souvent, car vos élèves auront des cartes différentes à chaque fois. C’est une bonne activité à utiliser à la fin d’une leçon lorsque tous les autres travaux sont terminés ; c’est une bonne manière d’utiliser les aptitudes de calcul mental.

Le jeu des nombres en triangle
Le jeu des nombres en triangle est le jeu mathématique le plus polyvalent pour les élèves d’âge primaire. Ce jeu se joue un peu comme les dominos : les nombres doivent être assortis pour créer un motif. Deux triangles sont mis côte à côte en fonction d’une règle définie d’avance. Dans l’exemple ci-dessous, la « règle » est que les deux nombres doivent donner 9 quand ils sont additionnés.
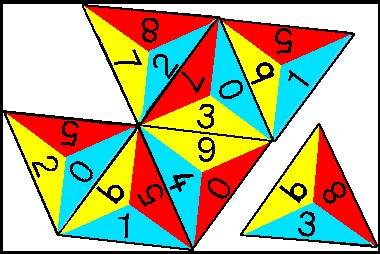
Pour les élèves plus âgés, le gagnant est celui qui termine ses cartes en premier, alors que les enfants plus jeunes jouent généralement de manière coopérative. Le nombre optimal de joueurs est de 2 à 4, mais le jeu peut aussi être utilisé par un seul joueur, comme une « patience ».
Certains de ces exemples ont été adaptés à partir de http://homepages.which.net/ ~jenny.murray/ games.htm
Si vous pouvez, consultez ce site web où vous trouverez d’autres idées et exemples.
Ressource 3: Tableau pour enregistrer les compétences en numération
![]() Ressource destinée à l’usage des élèves
Ressource destinée à l’usage des élèves
Cochez les aptitudes mathématiques utilisées dans chaque jeu, par exemple le jeu 1 fait appel à l’addition.
| jeu 1 | jeu 2 | jeu 3 | jeu 4 | jeu 5 | |
| nombres | |||||
| addition | ✓ | ||||
| soustraction | |||||
| multiplication | |||||
| division | |||||
| création d’ensembles | |||||
| |||||
|
Ressource 4: Le jeu culturel africain
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ce jeu porte de nombreux noms, par exemple :
- Kpo pour les Vai de Sierra Leone et du Liberia
- Ajua pour les Luo du Kenya
- Omweso pour les Ganda d’Ouganda
- Bao pour les Swahili d’Afrique orientale
- Gambatta en Ethiopie
- Ayo pour les Yoruba du Nigeria
- Oware pour les Ibo du Nigeria
- Warri pour les Asante du Ghana

Autrefois, ces jeux étaient en bois superbement sculpté, en bronze (à la cour royale du Bénin, au Nigeria) ou en or (pour les rois Asante du Ghana). Aujourd’hui, il existe des versions plus simples ; vous pouvez créer vos propres jeux avec un morceau de carton, en dessinant le nombre de cercles nécessaire.
REGLES DU JEU OWARE
L’objectif du jeu est de capturer plus de pions que votre adversaire.
Le support est composé de deux rangées de six cases, trous ou coupes. Une rangée appartient à chaque joueur. Il y a deux cases supplémentaires à l’extérieur du jeu lui-même, qui reçoivent les pions capturés (ou faits prisonniers) par chaque joueur.
Les pions sont tous identiques. On les appelle parfois pierres ou graines. Il y en a 48 en tout.
Au début du jeu, les 48 pions sont répartis également entre les 12 cases – quatre par case.
Pour jouer, un participant prend tous les pions se trouvant dans l’une des cases de sa rangée et, à partir de sa propre rangée jusqu’à celle de l’adversaire et en revenant à la sienne, en se déplaçant dans le sens contraire des aiguilles d’une montre, dépose les pions un par un, dans chaque case sur laquelle il passe, sans en sauter, jusqu’à ce qu’il n’ait plus de pions à déposer. Si le nombre de pions est suffisamment important, il peut revenir en un seul tour à la case où il a pris les pions initialement. Dans ce cas, il saute cette case, aucun pion n’y étant déposé, et le dépôt des pions se poursuit dans la case suivante.
Les participants jouent chacun à leur tour et doivent déplacer des pions à chaque tour.
Une capture se produit lorsque le dernier pion d’un tour est déposé dans une case du côté de l’adversaire et que le nombre de pions, après le dépôt, est de deux ou trois. Si la case avant la dernière est également passée à deux ou trois pions, ces pions sont également capturés et ainsi de suite pour chaque case précédente du moment que la rangée est celle de l’adversaire et qu’aucune case ne contient plus ou moins de deux ou trois pions.
Le jeu se termine lorsqu’un joueur, quand il prend son tour, s’aperçoit qu’il n’a pas de pions à déplacer, c'est-à-dire que toutes ses cases sont vides. Pour calculer les points, les pions restant sur le jeu sont ajoutés aux prisonniers du gagnant. Le joueur ayant le plus de prisonniers gagne.
Une règle exceptionnelle existe pour les cas où une rangée ne contient plus de pions. Si le joueur, lorsqu’il prend son tour, voit que son adversaire n’a plus de pions et qu’il peut déplacer des pions de manière à en laisser dans une ou plusieurs cases dans la rangée de l’adversaire, les règles du jeu l’obligent à déplacer des pions de cette manière. Si aucun déplacement de ce type n’est possible, le jeu est terminé, ou se termine lorsque l’adversaire prend son tour, comme l’indique le paragraphe précédent.
Lorsqu’il reste peu de pions en circulation, il est possible qu’aucune nouvelle capture ne puisse se produire : les pions se poursuivraient interminablement autour du jeu. Dans ce cas, les joueurs acceptent de mettre fin au jeu et le score est calculé d’après le nombre de prisonniers déjà constitués, plus les pions se trouvant dans les cases de chaque joueur.
Voilà les règles du jeu. Amusez-vous bien.
http://www.svn.net/rkovach/oware/how1.htm
Section numéro 2 : Structures des tableaux numériques
Question clé: Comment pouvez-vous utiliser des tableaux de nombres pour aider les élèves à identifier des structures dans les nombres ?
Mots clés: tableau de nombres ; structure de nombres ; multiplication ; étude ; travail de groupe ; opérations de base
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- aidé les élèves à identifier des structures au moyen de tableaux de nombres ;
- créé et géré des enquêtes en utilisant des tableaux de nombres ;
- amélioré vos aptitudes pour le travail en groupes.
Introduction
Un tableau des nombres jusqu’à 100 est une manière simple d’aider les élèves à identifier les structures des nombres et peut soutenir une large gamme d’activités d’apprentissage. Les tableaux de nombres peuvent être utilisés pour aider les jeunes élèves à compter, mais aussi pour réaliser des enquêtes ouvertes avec les élèves plus âgés ou plus aptes.
Dans cette section, vous aiderez vos élèves à comprendre les concepts mathématiques grâce à des enquêtes et des travaux en groupe.
1. Utilisation des tableaux de nombres
Il est important d’aider les élèves à acquérir de bonnes bases dans le fonctionnement des nombres pour faciliter leur éducation mathématique future. Dans cette partie, vous apprendrez à utiliser des questions-guides pour inciter les élèves à étudier un tableau de nombres et améliorer leurs aptitudes pour les opérations de base de la numération. En leur demandant de travailler en groupes, vous les aiderez à apprendre à coopérer. Ils devront aussi exprimer leur réflexion de manière explicite pour expliquer leurs idées aux autres.
Voir la ressource clé : Travailler en groupes dans la classe pour avoir des idées.
Étude de cas 1 : Utilisation des questions guide pour encourager l’analyse d’un tableau de nombres
M. Moussa au Togo souhaite aider ses élèves à étudier le fonctionnement des nombres en utilisant des tableaux de nombres à 100 cases (voir la Ressource 1 : tableau de nombres à 100 cases).
Il apporte des copies de tableaux à 100 cases dans la classe et répartit les élèves en groupes de quatre. Il distribue un tableau à chaque groupe. Il demande aux groupes d’étudier leur tableau, en notant les structures identifiées. Il pose des questions guides (voir la Ressource clé : Utiliser le questionnement pour développer la pensée), par exemple:
- Si vous suivez les rangées, que pouvez-vous dire à propos des nombres ?
- Quelle est la différence entre un nombre et celui qui se trouve à sa droite ?
- Quelle est la différence entre un nombre et celui qui se trouve en dessous ?
- Pouvez-vous identifier les multiples de 2 et les multiples de 5 dans le tableau ?
Pendant que ses élèves travaillent, M. Moussa se déplace dans la classe en vérifiant que tout le monde participe. Quand il remarque que certains élèves ont des difficultés, il les aide en leur suggérant des stratégies ou en leur posant des questions pour guider leur réflexion. 20 minutes plus tard, il remet la classe en un seul groupe. Il demande aux élèves d’expliquer les structures observées et d’essayer de formuler les règles de ces structures. Il les résume sur le tableau (voir la Ressource 1) pour aider tous les élèves à voir ce qu’ils ont fait.
Activité 1 : Quatre de suite
Préparez un tableau de nombres à 100 cases sur le tableau noir ou distribuez-en des copies à des groupes de quatre élèves dans la classe.
- Couvrez ou marquez quatre nombres consécutifs dans une rangée ou une colonne.
- Demandez aux groupes de créer des opérations. Les réponses doivent correspondre aux nombres cachés ou marqués.
Par exemple, si vous couvrez 10, 11, 12 et 13, les opérations pourraient être :
5+5=
13-2=
3x4=
9+4=
- Le premier groupe qui termine l’exercice pose les opérations et choisit un élève pour y répondre. Si toutes les opérations donnent la bonne réponse, le groupe obtient un point.
- Demandez à tous les autres groupes de partager leurs questions avec le groupe voisin. Si les questions sont correctes, le groupe obtient aussi un point.
- Continuer le jeu pendant 10 à 15 minutes pour que les élèves s’entraînent à créer des opérations.
La Ressource 2 : Réfléchir à votre leçon donne des exemples des types de questions qui vous aideront à évaluer cette activité. Utilisez ces questions ainsi que d’autres que vous pourriez imaginer pour réfléchir à l’activité – il peut être particulièrement utile d’effectuer cette réflexion avec un collègue.
2. Encourager les élèves à créer les questions pour leurs camarades
Les enquêtes qui permettent aux élèves de découvrir des informations par eux-mêmes ou en petits groupes sont des moyens efficaces de travailler sur les mathématiques.
La Ressource-clé : utilisation des enquêtes en classevous aidera à utiliser plusieurs techniques d’enquête. En demandant aux élèves de créer leurs propres questions simples, vous pouvez améliorer leurs capacités d’investigation. Cette partie explore les tableaux de nombres de manière différente, dans le but de développer la réflexion des élèves à propos des nombres et des structures.
Étude de cas 2: Se déplacer dans le tableau de nombres
Mme Agbogan souhaite donner plus d’assurance à ses élèves pour la réflexion mathématique. Elle prépare de nombreuses copies d’un tableau de nombres à 100 cases, elle répartit sa classe en groupes de deux élèves et distribue un tableau à chaque groupe. Elle pose ensuite les questions suivantes aux groupes, qui doivent y répondre en utilisant leur tableau :
- Comment pouvez-vous passer de 10 à 15 ? Par exemple, « en se déplaçant de 5 cases vers la droite ».
- Comment pouvez-vous passer de 10 à 35 ? Par exemple, « en se déplaçant de 5 cases vers la droite et de 2 cases vers le bas » ou bien « de 2 cases vers le bas et e 5 cases vers la droite ».
Elle parle avec la classe des différentes possibilités pour passer de 10 à 35 sur le tableau et aide les élèves à comprendre qu’il y a parfois plusieurs manières de répondre à la même question en mathématiques.
Mme Agbogan demande ensuite aux élèves de créer chacun dix questions similaires et d’y répondre chacun à leur tour avec leur partenaire, en s’aidant du tableau de nombres. Elle demande à ses élèves plus aptes d’essayer de créer des opérations.
Activité 2: Additions et soustractions à partir des tableaux de nombres
Avant la leçon, préparez des tableaux de nombres (voir la Ressource 1). Faites également les activités vous-même et identifiez le nombre de réponses différentes à chaque question.
- Demandez aux élèves de se mettre par deux, et distribuez un tableau à chaque groupe. Demandez-leur maintenant d’examiner des questions telles que :
- Combien y a-t-il de manières de passer de 21 à 34 sur le tableau ?
- Faites le tour de la classe en écoutant les raisonnements des élèves et en prenant des notes. Différents groupes de deux pourront donner des réponses différentes, par exemple : « Je descends de 1 case et j’avance de 3 cases » ou bien « j’avance de 3 cases et je descends de 1 case ».
- Demandez ensuite à vos élèves de créer chacun cinq questions similaires, pour passer d’une case à n’importe quelle autre, et de demander à leur partenaire de donner au moins deux réponses possibles à chaque question.
- Enfin, vous pouvez développer ce travail en demandant aux élèves de réfléchir avec leur partenaire pour répondre à la question : « Que se passe-t-il pour les dizaines et les unités dans chaque déplacement ? » Par exemple, quand on passe de 19 à 47 on descend de 3 rangées (on ajoute 30) et on se déplace de 2 colonnes vers la gauche (on soustrait 2). Cela revient au même que d’ajouter 28.
3. Travail simple d’investigation liant les tableaux numériques et multiplications
Dès que les élèves ont pris l’habitude de se déplacer dans le tableau de nombres, ils peuvent commencer à développer leurs aptitudes à « voir » ou visualiser des structures mathématiques. Un point de départ simple est de colorier (ou de masquer par des pions) toutes les cases qui répondent à un certain critère, par exemple les multiples d’un nombre spécifique. C’est ce qu’a fait l’enseignant dans l’Etude de cas 3.
Dans l’Activité clé vous supprimerez la plupart des cases (voir la Ressource 3 : tableaux de nombres partielspour avoir des exemples) et vous verrez si les élèves peuvent déduire quels nombres doivent se trouver dans des cases spécifiques.
Étude de cas 3: Étude de la multiplication avec les tableaux de nombres
Mme Dossou, enseignante d’une classe de 41 élèves du cours élémentaire deuxième année (4e année de primaire), distribue à des groupes de 4 élèves un tableau de nombres et 15 petites graines. Elle écrit au tableau
4, 6, 9, 11
et demande aux groupes de prendre un nombre à la fois et de placer une graine sur tous les multiples de ce nombre (par exemple, pour le nombre 4, les multiples sont 4, 8, 12, 16). Certains de ses élèves colorient ou hachurent les multiples au lieu d’y mettre des graines. Les élèves doivent alors noter par écrit les structures qu’ils peuvent identifier, comme elle le leur a montré avec le 4, avant de passer au nombre suivant. Elle leur demande de rechercher les structures dans les réponses :
4
8
12
16
20
24
28
32
36
40
Elle demande à un groupe différent à chaque fois de montrer ses réponses ; ce groupe parle alors des structures se trouvant dans le tableau et dans les réponses.
Pour voir un exemple du travail fait par la classe de Mme Dossou, voir la Ressource 4 : Les tableaux de multiplication de Mme Dossou.
Activité clé : Utilisation d’un tableau de faits de multiplication
Pour renforcer le travail précédent, demandez à vos élèves de mener une enquête en utilisant des tableaux de faits de multiplication. Avant la leçon, préparez un grand tableau de faits sur les nombres pour 5, 6, 7, 8 et 9, en laissant certaines cases vides. Vous allez demander à vos élèves de trouver les numéros manquants en se servant des connaissances qu’ils possèdent déjà.
- Répartissez vos élèves en groupes de quatre ou cinq et demandez à chaque groupe de recopier votre tableau.
- Demandez aux élèves de déterminer ensemble les numéros manquants et, quand ils sont d’accord, de remplir leur exemplaire et d’afficher leurs résultats. Pendant qu’ils travaillent, déplacez-vous dans la classe en écoutant et en aidant – uniquement lorsque c’est absolument nécessaire – en posant des questions au lieu de donner des réponses.
- Quelles informations connaissez-vous ?
- Quels numéros manquent ?
- Pouvez-vous voir une structure dans la rangée ? Dans la colonne ?
- Demandez à un membre de chaque groupe d’expliquer comment le groupe a trouvé les réponses et organisez un débat avec toute la classe pour décider quelle est la solution correcte.
- Demandez à chaque groupe de réaliser une copie propre d’un tableau de multiplication et d’indiquer clairement les multiples. Affichez chaque tableau dans la classe, dans l’ordre, de la table de multiplication par 2 à la table de multiplication par 10 pour que les élèves puissent voir facilement les structures.
Enfin, consultez les questions de la Ressource 2 pour vous aider à réfléchir à la réussite de la leçon.
Ressource 1 : Tableau de nombres à 100 cases
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Un tableau de nombres à 100 cases est simplement une grille de 10 cases de côté, les cases étant numérotées par lignes en commençant par « 1 » en haut à gauche.
Il se peut que vous puissiez acheter un grand tableau de nombres sur lequel vous pourrez écrire à la craie. Vous pouvez aussi en imprimer un à partir de cette ressource ou en créer un vous-même.
Voici des exemples de règles que les élèves peuvent facilement découvrir tout en travaillant avec le tableau de nombres à 100 cases :
- Pour monter d’une ligne, soustraire 10
- Pour descendre d’une ligne, ajouter 10
- Pour se déplacer d’une case vers la gauche, soustraire 1
- Pour se déplacer d’une case vers la droite, ajouter 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Ressource 2 : Réflexion sur votre leçon
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
A la fin de toute session d’enseignement, il est toujours recommandé de faire une pause et de réfléchir au déroulement de la leçon. En vous posant quelques questions et en y répondant honnêtement, vous approfondirez votre réflexion à propos de vos rôles et responsabilités en tant qu’enseignant.
Voici quelques questions pour vous aider à réfléchir à ce qui s’est bien passé et aux domaines que vous pourriez améliorer ou développer.
- Les premiers travaux avec le tableau de nombres ont-ils donné de bonnes bases pour les leçons suivantes ? Comment cela s’est-il produit ?
- Les élèves ont-ils aimé cette enquête ? Comment savez-vous qu’ils l’ont aimée ?
- Tous les élèves ont-ils participé ? Dans la négative, comment pourriez-vous faire en sorte que tout le monde participe la prochaine fois ?
- Avez-vous eu l’impression de contrôler la classe ?
- Comment pourriez-vous améliorer cette leçon ?
- Des groupes plus petits seraient-ils préférables ? Pourquoi ?
- Avez-vous donné assez de temps aux élèves pour faire les tâches ?
- Avez-vous donné à tous les élèves la possibilité de parler de ce qu’ils avaient fait ?
- Qu’est-ce que les élèves ont appris ?
Ressource 3 : Tableaux partiels de nombres
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
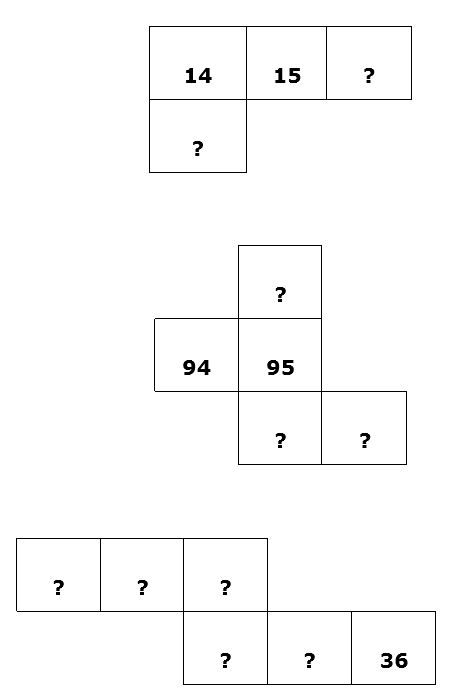
- Les élèves peuvent-ils remplir les nombres manquants ?
- Demandez-leur d’expliquer comment ils ont réussi à le faire.
Voyez si les élèves peuvent créer et résoudre leurs propres puzzles de « nombres manquants ».
Ressource 4 : Les tableaux de multiplication de Mme Dossou
![]() Exemple de travaux d’élèves
Exemple de travaux d’élèves
Voici un tableau de multiplication rempli par un élève dans la classe de Mme Dossou. Il indique les multiples de 4.
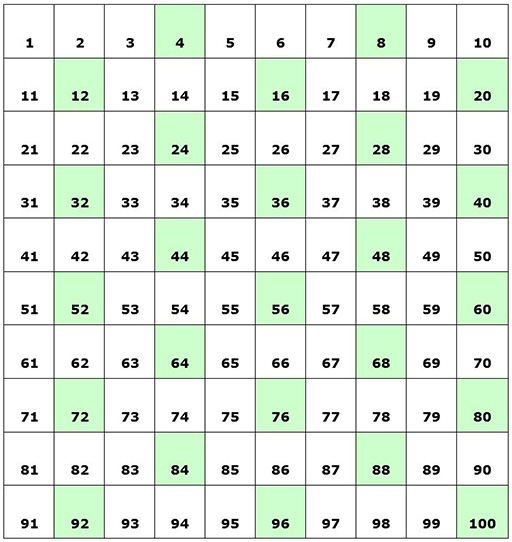
Section numéro 3 : Comment résoudre les problèmes numériques
Question clé: Comment pouvez-vous développer les aptitudes de résolution de problèmes des élèves en utilisant des problèmes numériques ?
Mots clés: métacognition ; différenciation ; tâches ; créativité ; « réfléchir à la réflexion » ; résolution de problèmes ; nombre
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- utilisé des stratégies pour explorer les moyens employés par les élèves pour résoudre des problèmes mathématiques ;
- fait la distinction entre les caractéristiques profondes et superficielles des problèmes mathématiques ;
- utilisé des techniques pour développer la « réflexion sur la réflexion » chez vos élèves.
Introduction
La résolution de problèmes est une manière intéressante de développer la réflexion mathématique de vos élèves. Les élèves doivent réfléchir aux calculs devant être faits avant de pouvoir trouver la réponse. Ils doivent donc trier les informations fournies pour définir les éléments dont ils ont besoin pour trouver la réponse et pour trouver la méthode à utiliser.
Ceci les aidera à exprimer leur réflexion mathématique et à comprendre et reconnaître les caractéristiques profondes d’un problème mathématique. Il vous sera peut-être utile de réfléchir aux raisons pour lesquelles la résolution des problèmes est importante. Certaines raisons sont fournies dans la Ressource 1 : Pourquoi la résolution des problèmes est importante.
1. Il existe plusieurs solutions à un même problème : aider les élèves à réfléchir et à verbaliser leurs réponses
« Réfléchir sur la réflexion » ou métacognition est un moyen puissant pour aider les élèves à comprendre et reconnaître les caractéristiques « profondes » de types de problèmes particuliers et à identifier la manière de résoudre de tels problèmes.
La première étape de cette réflexion est de donner aux élèves l’opportunité de parler des problèmes qu’ils tentent de résoudre et des méthodes qu’ils emploient pour tenter de les résoudre. Lorsque les élèves expliquent leur réflexion, il faut les écouter et ne pas rejeter leurs idées.
Il existe de nombreuses manières différentes de résoudre les problèmes mathématiques (voir la Ressource 1). Vous serez peut-être surpris du nombre de moyens identifiés par les élèves auxquels vous n’attendiez pas.
Étude de cas 1 : Ecouter la voix des élèves en mathématiques
Nèmè au Togo rappelle à ses élèves que lorsqu’ils rentrent chez eux après l’école, il n’existe pas qu’un seul chemin : il y a de nombreux chemins possibles. Certains sont plus courts, d’autres plus longs, certains plus sûrs, d’autres plus intéressants. Elle leur dit que c’est la même chose pour les problèmes mathématiques – il y a souvent plus d’une manière d’arriver à la bonne réponse et il est peut-être intéressant d’examiner les différentes manières.
Nèmè écrit les questions suivantes au tableau :
- Djif a 24 pierres. Il donne 9 pierres à un ami. Combien lui reste-t-il de pierres ?
- Rafiatou mange 7 bonbons chaque jour. Elle a 42 bonbons. Combien de jours vont durer ses bonbons ?
- L’institutrice achète 25 paquets de crayons. Il y a 12 crayons dans chaque paquet. Combien de crayons a-t-elle ?
Elle demande ensuite aux élèves de répondre aux questions en utilisant la méthode de leur choix. Elle donne aux élèves dix minutes pour répondre aux questions. Elle vérifie leurs réponses puis demande à un ou deux d’entre eux d’expliquer comment ils sont arrivés à chaque réponse.
Nèmè répertorie ces méthodes pour trouver les réponses et note les méthodes les plus utilisées. Elle rappelle à ses élèves les différents chemins pour rentrer de l’école.
Activité 1 : Aider les élèves à réfléchir
Essayez cette activité vous-même d’abord, de préférence avec deux collègues ou plus. Essayez-la ensuite avec vos élèves.
- Demandez à vos élèves d’essayer de répondre aux trois questions de Nèmè en travaillant individuellement.
- Répartissez la classe en groupes de quatre ou cinq élèves et demandez-leur d’expliquer soigneusement chacun à leur tour entre eux comment ils ont obtenu leurs réponses.
- Demandez ensuite aux groupes de dresser une liste des stratégies utilisées puis posez ces questions :
- Aviez-vous tous la même réponse ?
- Y êtes-vous arrivés de la même manière ?
- Combien de manières différentes votre groupe peut-il trouver pour arriver à la réponse correcte à chaque question ?
- Ecrivez-les au tableau.
Expliquez à vos élèves qu’il est important d’essayer différentes manières de résoudre des problèmes afin d’aider leur réflexion mathématique.
2. Identifier les caractéristiques profondes et les caractéristiques superficielles de problèmes de mathématiques
Toute tâche ou problème mathématique que vous posez à vos élèves contient des caractéristiques « profondes » - celles qui définissent la nature de la tâche, et des stratégies qui peuvent faciliter sa résolution.
Pratiquement tous les problèmes mathématiques possèdent ces caractéristiques profondes, recouvertes d’un ensemble spécifique de caractéristiques superficielles. En tant qu’enseignant, vous devez aider vos élèves à comprendre que lorsqu’ils ont reconnu les caractéristiques superficielles, leur changement n’a aucune influence sur la manière de résoudre le problème. Les stratégies de résolution d’un problème restent les mêmes. (Voir la Ressource 2 : manières d’aider les élèves à résoudre des problèmes.)
Étude de cas 2: L’essence du problème
Eméfa Adjavon écrit ce problème au tableau :
Dans une famille, il y a deux enfants : Mendièb a 8 ans et Kékéli a 4 ans. Quel est l’âge moyen des enfants ?
Certains élèves veulent immédiatement répondre à la question mais Eméfa leur dit qu’avant de chercher la réponse elle veut qu’ils examinent soigneusement la question – le type de question. Y a-t-il quelque chose qu’elle pourrait changer sans que cela change le résultat ?
Certains élèves s’aperçoivent qu’on peut changer le nom des enfants sans changer le résultat. Eméfa les félicite.
Elle écrit une opération simple au tableau (1+1=2) puis dit « Si je change les nombres » (elle écrit alors 2+5=7) « ce n’est pas la même opération mais c’est toujours le même type d’opération. Dans notre question sur la moyenne, qu’est-ce que nous pourrions changer sans modifier le type d’opération ? »
Certains élèves suggèrent qu’ils peuvent changer l’âge des enfants et les noms.
Eméfa leur demande alors : « Est-ce que ce serait un type d’opération différent si nous parlions de vaches au lieu d’enfants ? »
Ils continuent à dialoguer ainsi jusqu’à ce qu’ils s’aperçoivent qu’ils peuvent changer la chose considérée, le nombre et la propriété des choses comptées, tout cela sans changer le type d’opération réalisé.
Les élèves commencent alors à créer et à répondre à autant d’exemples différents de ce type d’opération qu’ils peuvent imaginer.
Activité 2: Qu’est-ce qui peut changer ? Qu’est-ce qui doit rester identique ?
Essayez d’abord cette activité vous-même.
Ecrivez la question suivante au tableau noir :
M. Aziati construit un mur en blocs de ciment d’un côté de son terrain pour empêcher les chèvres d’y rentrer. Son mur fait 10 blocs de haut et 20 blocs de long. Combien de blocs lui faudra-t-il au total ?
- Demandez à votre classe de résoudre le problème.
- Vérifiez la réponse.
- Demandez ensuite à vos élèves, en groupes de quatre ou cinq, de discuter ensemble de la réponse et de chercher ce que l’on pourrait changer dans le problème tout en le gardant essentiellement similaire, pour pouvoir le résoudre de la même manière.
- Demandez au groupe de créer un autre exemple, essentiellement le même, pour ne pas changer la tâche de base.
- Echangez le problème d’un groupe avec celui d’un autre et demandez au nouveau groupe de trouver la solution.
- Doivent-ils résoudre ce nouveau problème de la même manière ?
3. Réfléchir à ce qui rend les problèmes faciles ou difficiles
La résolution des problèmes peut être adaptée pour que chaque élève participe. Par exemple, tous les élèves peuvent parler des aspects qui rendent un problème facile ou difficile à résoudre. Ce sont parfois les variations des caractéristiques superficielles – par exemple l’utilisation de grands nombres, de décimales ou de fractions au lieu de petits nombres entiers – qui rendent un problème plus difficile à résoudre.
Parfois, la mise d’une question dans un « contexte » facilite la résolution, mais dans d’autres cas cela peut distraire les élèves des caractéristiques profondes du problème et les empêcher de voir aussi facilement la manière de le résoudre.
Lorsque les élèves commencent à identifier les caractéristiques profondes d’un problème, ils commencent aussi à « voir au-delà » des caractéristiques superficielles et reconnaissent la tâche sous-jacente. Les élèves peuvent alors s’attaquer avec assurance à toute tâche comportant les mêmes caractéristiques profondes. Voir la Ressource 2 pour les facteurs importants que vous devez prendre en compte lorsque vous donnez et solutionnez des problèmes avec votre classe.
Étude de cas 3: Augmenter la facilité, augmenter la difficulté
Ablavi travaille avec ses élèves sur le thème de la division.
Elle écrit trois problèmes de division au tableau :
- Aboè a 12 oranges et 3 enfants. S’il partage les oranges de manière égale, combien d’oranges recevra chaque enfant ?
- Divisez 117 par 3.
- Kafui a 312 francs pour aller au travail. Elle dépense 52 francs par jour pour le taxi. Un jour, il ne lui reste pas assez d’argent pour le taxi. Combien de jours est-elle allée travailler ? Le jour où elle n’a pas assez d’argent, combien d’argent de plus lui faut-il pour le taxi ce jour là ?
Elle demande à ses élèves, en groupes de quatre, d’essayer de résoudre ces problèmes ensemble.
Dix minutes plus tard, Ablavi demande à ses élèves quels étaient les problèmes plus faciles ou plus difficiles à résoudre. Ensemble, ils font deux listes au tableau – « les choses qui rendent les problèmes difficiles » et « les choses qui rendent les problèmes faciles ».
Ablavi demande aux groupes de trouver combien de manières différentes ils peuvent utiliser pour résoudre les problèmes. Elle annonce qu’elle récompensera le groupe qui trouvera le plus de manières différentes en affichant un certificat « champions en maths » avec leur nom sur le mur de la classe.
Activité clé : Les élèves créent leurs propres tâches
- Avec votre classe, faites une liste au tableau des « choses qui rendent les problèmes difficiles » et des « choses qui rendent les problèmes faciles ».
- Demandez à vos élèves, en groupes, de créer trois questions. Ils doivent créer une question facile, une question plus difficile et une question très difficile.
- Dix minutes plus tard, demandez aux groupes d’échanger les problèmes qu’ils viennent de créer avec un autre groupe et de résoudre les questions que l’autre groupe leur a données.
- Demandez aux groupes de vous présenter leurs conclusions. Les questions « très difficiles » étaient-elles vraiment bien plus difficiles que les questions « faciles » ? Qu’est-ce qui rend les questions difficiles ou faciles ? Revenez sur les listes écrites au tableau – y a-t-il des choses que les élèves veulent changer ou ajouter maintenant à propos de ce qui rend les problèmes difficiles ou faciles ?
- Demandez-leur, comme devoirs à la maison, de créer des problèmes liés à leur communauté locale, par exemple le nombre d’arbres, le prix d’un taxi.
- Le lendemain, partagez-les en classe et demandez aux élèves de les résoudre.
Ressource 1 : Pourquoi la résolution des problèmes est importante
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
La résolution des problèmes :
- rend les leçons de mathématiques plus agréables et intéressantes ;
- aide les élèves à prendre confiance en leurs propres aptitudes mathématiques ;
- aide les élèves à voir qu’il existe une interaction entre les mathématiques et la vie quotidienne ;
- aide les élèves à apprécier l’apprentissage des mathématiques ;
- améliore les aptitudes de communication en mathématiques ;
- développe le processus de création et d’essai d’hypothèses ;
- développe la réflexion abstraite.
Stratégies pour résoudre les problèmes
- Dessiner une image ou un diagramme.
- Faire un tableau.
- Faire une liste.
- Rechercher une structure.
- Deviner et vérifier.
- Enoncer le problème d’une autre manière.
- Examiner toutes les possibilités de manière systématique.
- Travailler à l’envers.
- Résoudre un problème plus simple avec moins de variables.
- Explorer le rôle de chaque variable une par une en fixant les autres.
- Explorer les problèmes similaires précédents.
- Rechercher les caractéristiques « profondes ».
Ressource 2 : Manières d’aider les élèves à résoudre des problèmes
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
Vous pouvez aider vos élèves à prendre confiance en eux pour résoudre des problèmes en les aidant à comprendre l’importance des éléments suivants :
- lire le problème soigneusement pour identifier les parties importantes ;
- identifier les caractéristiques « profondes » d’un problème ;
- décider quels sont les éléments exacts qui entrent en jeu ;
- discuter et partager différentes méthodes pour résoudre le problème ;
- essayer différentes idées ;
- travailler seul et avec d’autres ;
- être prêt à recommencer en cas d’erreur ;
- vérifier son travail ;
- demander de l’aide à d’autres élèves ou à l’enseignant quand c’est nécessaire.
Vous pouvez aussi aider vos élèves à prendre confiance en eux pour résoudre des problèmes en :
- utilisant des contextes qui intéressent les élèves lorsque vous créez des problèmes ;
- créant un environnement de classe favorable, pour leur permettre de partager des idées sans craindre qu’on se moque d’eux.
Section numéro 4 : Visualisation de la multiplication
Question clé: Comment pouvez-vous aider les élèves à identifier des structures dans les nombres ?
Mots clés: visualisation ; multiplication ; forme ; imagination ; séquence ; planification ; travail en groupe
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- exploré la multiplication avec vos élèves par des moyens visuels ;
- utilisé des formes rectangulaires pour aider les élèves à comprendre les facteurs ;
- utilisé des enquêtes pour explorer les structures des séries de nombres.
Introduction
La capacité à « voir » ou visualiser les structures mathématiques est une aptitude de base permettant de développer la compréhension. Il peut également s’agir d’un processus excitant de découverte alors que les élèves apprennent à voir les nombres et les formes de nouvelles manières.
Cette section vous montre des manières d’aider vos élèves à « voir » des formes et structures dans les nombres.
1. Travailler en binômes sur les nombres carrés
Le concept des « nombres carrés » peut sembler très abstrait. Le fait de dessiner des carrés, ou de créer des carrés avec des pions, peut aider les élèves à commencer à les comprendre visuellement. Quel nombre de pions faut-il pour créer des formes carrées (c'est-à-dire celles qui ont des nombres égaux de pions sur chaque ligne, et autant de lignes que de colonnes) ?
Vous devez préparer vos leçons pour que tous les élèves participent. Dans l’Activité 1, vous demanderez à vos élèves de travailler par deux.
Étude de cas 1: Dessiner des nombres carrés
Mme Essodina du Togo souhaite que ses élèves mènent des enquêtes par deux, en leur donnant seulement quelques conseils. Elle désire voir si les élèves peuvent étudier eux-mêmes les nombres carrés.
Elle commence la leçon en demandant aux élèves de travailler par deux. Elle dessine un carré au tableau ; elle dessine ensuite un carré plus grand fait de quatre plus petits carrés (voir la Ressource 1 : les nombres carrés). Elle demande aux élèves de dessiner le plus possible d’autres carrés comme ceux-ci en cinq minutes. Elle explique à la classe que ces nombres s’appellent des « nombres carrés ».
Mme Essodina demande aux élèves s’ils peuvent trouver plus de nombres carrés et leur demande de noter le nombre de petits carrés nécessaires pour créer chaque grand carré.
En permettant aux élèves de travailler avec un maximum d’autonomie, Mme Essodina pense qu’ils prendront de l’assurance et qu’ils trouveront la leçon agréable. Elle s’aperçoit que la plupart des groupes travaillent bien ensemble.
Activité 1 : Créer des nombres carrés avec des objets
Examinez la tâche de la Ressource 1. Lisez-la soigneusement et essayez la tâche vous-même avant de la réaliser avec votre classe.
Encouragez chaque élève à participer en demandant aux groupes de deux de choisir d’abord celui qui sera le scribe (celui qui dessinera) et celui qui enregistrera les informations, puis d’échanger ces tâches. De cette manière, vous serez sûr que tous les élèves participeront.
Vous pouvez aussi distribuer des objets à vos élèves (des graines ou de petits cailloux) comme pions. Demandez à des paires d’élèves de trouver des « nombres carrés » (ceux qui ont des nombres égaux de pions sur chaque ligne et autant de lignes que de colonnes).
2. Utilisation de jeux pour explorer les nombres rectangulaires
Des nombres carrés nous passons aux nombres rectangulaires. La seule exigence pour ces nombres est d’avoir au moins 2 lignes et 2 colonnes. Chaque ligne doit avoir le même nombre de croix, par exemple :
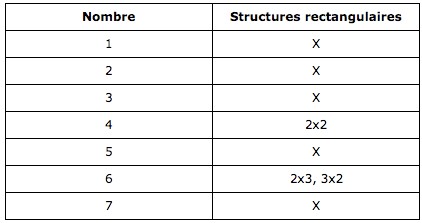
Ceci permet d’illustrer les nombres « rectangulaires ». Pensez-vous qu’il y a plus ou moins de nombres « rectangulaires » que de nombres « carrés », et pouvez-vous expliquer pourquoi ?
L’examen des nombres qui créent des formes rectangulaires est une manière pour les élèves d’explorer la multiplication (ou la division) en voyant et en faisant, ainsi qu’en réalisant des opérations mentales et écrites.
Essayez les enquêtes vous-mêmes pour voir quelles difficultés les élèves risquent de rencontrer et réfléchissez aux manières d’aider ceux qui ont des problèmes – vous serez ainsi plus efficace pour soutenir leur apprentissage.
Étude de cas 2: Faire un jeu pour trouver les facteurs
Mme Ali prévoit de demander à ses élèves de trouver différents nombres rectangulaires en utilisant les faits de la multiplication.
Elle décide d’organiser un concours dans la classe. Elle divise la classe en deux équipes et demande à chaque équipe de choisir un marqueur. Le jeu est le suivant : elle écrit un nombre au tableau et le premier élève lui donnant deux facteurs corrects pour ce nombre marque un point pour son équipe. Mme Ali explique qu’il y a plus d’une réponse correcte – quelquefois il y en aura beaucoup. Elle donne alors un exemple en écrivant 6 et en expliquant qu'elle aurait donné un point à tout élève lui disant "2 fois 3" ou "3 fois 2" ou "1 fois 6" ou "6 fois 1". Les élèves aiment le jeu et participent avec excitation. Mme Ali est très heureuse car elle a prévu à l’avance que ce jeu aidera ses élèves à faire l’activité suivante.
Par la suite, elle joue souvent à ce jeu avec ses élèves lorsqu’elle a cinq minutes à la fin de la journée.
Activité 2: La multiplication avec des pions
Il vous faut 20 pions, ou 20 capsules de bouteille, ou 20 cailloux pour chaque groupe de quatre ou cinq élèves.
- Commencez par répartir la classe en groupes et distribuez les pions.
- Copiez ou dessinez le tableau de la Ressource 2 : Table de multiplications au tableau pour que chaque élève copie ou enregistre ses résultats.
- Demandez aux groupes de prendre 6 pions et de les placer en lignes de nombres égaux, en explorant toutes les possibilités.
- Cinq minutes plus tard, demandez aux groupes de partager toutes les possibilités identifiées pour le nombre 6. Vérifiez qu’au moins un groupe a inclus une seule ligne. Demandez aux groupes de remplir leur tableau pour le nombre 6, comme illustré dans la Ressource 2.
- Ensuite, laissez-les essayer le nombre 12 mais, mais avant de commencer à aligner leurs pions ils doivent prédire le nombre de possibilités puis vérifier si leurs prédictions sont justes.
- Répétez la même procédure avec tous les nombres du tableau.
3. Observer et inventer des modèles numériques liés à la multiplication
Dans cette partie, nous examinons une autre manière d'identifier les structures de la multiplication, qui n’est pas basée sur les formes et les pions mais qui recherche malgré tout les structures dans les lignes et colonnes. Le fait d’aider les élèves à explorer les structures par des activités pratiques développe leur réflexion approfondie.
Imaginez deux colonnes, une pour les « dizaines » et l’autre pour les « unités ». Si nous pensons par exemple à la table de 8, les quatre premiers chiffres sont 8, 16, 24, 32.
Que deviennent les dizaines et les unités dans les deux colonnes ? Vous devez remarquer que les dizaines augmentent de 1 à chaque fois alors que les unités diminuent de 2. En utilisant cette observation, pouvez-vous dire quels seraient les trois nombres suivants ? Voir la Ressource 3 : Dizaines et unités pour avoir un exemple de cet exercice.
Des observations et questions comme celles-ci peuvent être utilisées pour aider les élèves à apprendre les multiplications et à reconnaître les structures.
Étude de cas 3 : Reconnaître les structures des séquences
M. Abalo souhaite organiser une activité d’exploration des nombres. Il écrit les séquences de nombres suivantes au tableau puis demande aux élèves de l'aider à trouver le nombre manquant. Les élèves doivent lever la main et dire quel est le nombre manquant et pourquoi.
- 4, 6, 8, , 12, 14
- 3, 6, , 12, 15
- 16, 25, , 49, 64
- 1, 11, 111, , 11111
- 1, 1, 2, 3, , 8, 13
Lorsque les élèves ont terminé, il leur demande de créer leurs propres structures et d’omettre un nombre. Ils échangent alors leur structure avec leur partenaire et essaient de trouver les nombres manquants.
Les élèves sont enthousiastes et aiment cette activité. M. Abalo leur demande s’ils voient une structure ? Peuvent-ils prédire le dernier nombre et chaque réponse ? Il est content de voir que certains le peuvent.
M. Abalo utilise souvent le travail par deux car il permet à tous les élèves de participer et favorise leur réflexion.
Activité clé : Exploration des multiples de 9
Vous aurez besoin de la Ressource 4 : Table de multiplication
- Tenez-vous devant le tableau et demandez aux élèves de se taire. Demandez-leur de regarder attentivement.
- Ecrivez les cinq premiers multiples de 9 au tableau.
- Faites une pause. Demandez-leur de regarder ce qui arrive aux nombres.
- Demandez à un élève de terminer la série jusqu’à 10 x 9 sous le titre « dizaines » et « unités ».
- Demandez aux élèves de partager tout ce qu’ils remarquent, en notant et acceptant toutes les suggestions sans faire de commentaires.
- Continuez, mais arrêtez-vous après 13 x 9, sautez quelques niveaux puis écrivez 17 x 9 = ? Observez les élèves soigneusement pendant qu’ils essaient de comprendre ce qui se passe. Vous devrez peut-être les aider en leur disant d’observer la structure des dizaines et des unités.
Enfin, demandez à des groupes de deux élèves d’examiner d’autres multiples (il est préférable de commencer avec les chiffres de 1 à 9). Peuvent-ils trouver ensemble la structure des dizaines et des unités ?
Ressource 1 : Les nombres carrés
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
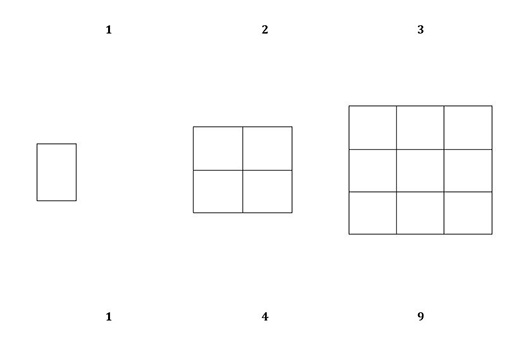
- Dessinez d’abord un carré au tableau en indiquant « 2 cm » pour les côtés et divisez-le comme illustré en carrés de 1 cm.
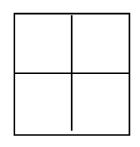
- Le premier élève chargé de l’enregistrement doit compter les carrés de 1 cm et écrire le résultat.
- Le premier scribe doit dessiner un carré de 3 cm et le diviser de la même manière en carrés de 1 cm ; l’enregistreur doit alors compter et enregistrer ces petits carrés.
- Cette activité continue avec un carré de 4 cm, un carré de 5 cm et un carré de 6 cm.
- Exemples
Exemples

Demandez aux groupes de deux de dessiner d’autres nombres carrés jusqu'à cent. Les groupes de deux dessinent, comptent et enregistrent les nombres chacun à leur tour.
Ressource 2 : Tableau de multiplications
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
| Le nombre | Les possibilités | Nombre de possibilités |
| 3 | ||
| 4 | ||
| 6 | (1 x 6) (2 x 3) (3 x 2) (6 x 1) | 4 |
| 8 | ||
| 9 | ||
| 10 | ||
| 12 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 18 | ||
| 20 |
Ressource 3 : Les dizaines et les unités
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Demandez à vos élèves de remplir les trois lignes suivantes de nombres dans ce tableau.
| Dizaines | Unités |
| 0 | 8 |
| 1 | 6 |
| 2 | 4 |
| 3 | 2 |
| ? | ? |
| ? | ? |
| ? | ? |
Ressource 4 : Table de multiplication
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
(Exemple : table de 9)
1 x 9 = 9
2 x 9 = 18
3 x 9 = 27
4 x 9 = 36
5 x 9 = 45
6 x 9 = 54
7 x 9 = 63
8 x 9 = 72
9 x 9 = 81
10 x 9 = 90
11 x 9 = 99
12 x 9 = 108
13 x 9 = 117
14 x 9 = 126
#
#
17 x 9 = ?
Les unités diminuent de un à chaque ligne, alors que les dizaines augmentent de un, sauf entre 10 x et 11 x
Quand on ajoute les chiffres du résultat de la multiplication, le total est 9.
Section numéro 5 : Travail pratique avec les fractions
Question clé: Comment pouvez-vous aider les élèves à comprendre les fractions ?
Mots clés: bandes de fractions ; disques de fractions ; opérations simples ; travail en groupe ; résolution de problèmes ; définition ; numérateur
Résultats de l’apprentissage
À la fin de cette section, vous aurez :
- permis aux élèves de mieux comprendre les fractions en utilisant des ressources simples ;
- utilisé le travail en groupe et la résolution de problèmes pour donner de l'assurance aux élèves en ce qui concerne les fractions.
Introduction
Le fait d’autoriser les élèves à diviser des choses en « parties d’un tout » en utilisant des objets réels les aide à passer plus facilement à des idées abstraites comme les fractions, la division, les quotients et les proportions. Cette section vous aide à utiliser des objets physiques simples et des activités pratiques pour développer la compréhension de ces concepts chez vos élèves.
1. Explorer les fractions simples en groupes, avec des ressources simples
Dans cette section, vous allez introduire le concept des fractions. Essayez les tâches avec des groupes de taille différente - vous identifierez ainsi l’organisation la mieux adaptée à votre situation et à chaque tâche pratique. Pour avoir un complément d’information, consultez la Ressource clé : Travailler en groupe dans la classe.
Étude de cas 1 et Activité 1 utilisent des ressources simples – un fruit, du papier et des bandes de fractions pour aider les élèves à comprendre plus facilement le concept des fractions. Le travail en groupe et le fait de demander aux élèves de discuter leurs conclusions permettent de les exposer à différentes fractions. La compréhension des fractions fournit des bases pour réfléchir à la division (« partager en » parts égales est la première étape dans la compréhension de la division), aux quotients, aux proportions et aux chiffres décimaux.
Vous souhaiterez peut-être revoir vos propres connaissances des fractions en étudiant la Ressource 1 : Fractions.
Étude de cas 1 : Utiliser le travail en groupe pour explorer des fractions simples
M. Kolani au Togo commence sa leçon dans sa classe de cours moyen première année (5e année de primaire) en découpant une orange en deux parts égales puis en quatre parts égales, en demandant aux élèves de nommer les parts: moitiés puis quarts.
Il introduit des fractions simples, en illustrant chacune en pliant des rectangles de papier. Il souligne que deux moitiés forment un tout etc.
Il parle alors avec les élèves de la manière dont les choses sont partagées dans la vie réelle. Comme sa classe est chargée, il la divise en petits groupes de trois. Il dessine un cercle, un rectangle et un carré au tableau et demande à chaque élève de choisir une forme et de la dessiner six fois. Il demande aux élèves de hachurer leurs dessins pour indiquer
- une moitié
- deux moitiés
- un quart
- deux quarts
- trois quarts
- quatre quarts
Chaque élève du groupe montre alors aux autres ce qu’il a fait. M. Kolani leur demande s’ils voient des structures dans leurs dessins et certains élèves déclarent que deux quarts est la même chose qu'une moitié etc. Ils partagent ces informations avec les autres membres de leur groupe et avec la classe.
La classe de M. Kolani était chargée mais il s’est aperçu que sa technique de travail en groupes permettait à tous les élèves de comprendre les bases des fractions équivalentes à partir de leurs dessins et de l’interaction avec les autres élèves. Il a également conclu que les élèves étaient bien préparés pour la leçon suivante.
Activité 1 : Utilisation des bandes de fractions
Répartissez les élèves en groupes de quatre. Distribuez aux groupes quatre bandes de papier de même longueur (voir la Ressource 2 : Bandes de fractions). Dans chaque groupe, demandez à un élève de plier une bande en deux parties égales ; un autre élève doit plier une bande en 4 et un autre en 8. Un élève du groupe ne doit pas plier sa bande.
En utilisant les bandes, les élèves doivent répondre à ces questions:
- Combien de moitiés (1/2) font un tout ?
- Combien de quarts (1/4) font une moitié (1/2) ?
- Combien de huitièmes (1/8) font un quart (1/4) ?
Vous pouvez alors leur demander d’essayer des fractions équivalentes plus difficiles, par exemple :
- Combien de huitièmes (1/8) y a-t-il dans une moitié (1/2) ?
- Combien de huitièmes (1/8) y a-t-il dans trois quarts (3/4) ?
Pendant que les élèves travaillent, circulez pour les aider. Partagez certaines des réponses avec la classe pour montrer comment fonctionnent les fractions.
2. Utiliser des bandes et des cercles de fractions pour faire des additions et soustractions de fractions
Dans cette partie, nous poursuivons le travail déjà fait avec les bandes de fractions, pour additionner et soustraire des fractions simples.
Pendant que vous travaillez, posez-vous ces questions :
- Devez-vous aider beaucoup vos élèves ? Si c’est le cas, pourquoi ?
- Est-ce que vous et les élèves aimez faire ces activités pratiques ?
- Pensez-vous que les élèves apprennent plus de cette manière que si vous leur faisiez une leçon classique ? Comment est-ce que vous le savez ?
Étude de cas 2: Autres activités avec les bandes de fractions
M. Kolani apporte dans sa classe une grande bande de fractions de dixièmes qu’il a réalisée ; il demande à chaque élève d’en faire une similaire avec les ressources qu’il fournit. 15 minutes plus tard, il aide les élèves à utiliser leurs bandes de fractions pour trouver des réponses à ces questions :
- 8/10 est plus grand que 5/10, mais de combien ?
- Quelle est la différence entre 8/10 et 5/10 ?
- Quel est le résultat de 8/10 – 5/10 ?
Il écrit au tableau l’opération 8/10 – 5/10 = 3/10 et demande aux élèves de la recopier dans leurs cahiers d’exercices.
Il demande alors à ses élèves de travailler par deux pour faire des additions avec des dixièmes en utilisant leurs bandes de fractions. Il crée des opérations pour eux et demande à ceux qui travaillent bien de créer des opérations les uns pour les autres.
M. Kolani était très surpris des capacités des élèves mais s’est aussi aperçu qu’il devait donner à ses élèves plus d’occasions de s’entraîner et du temps pour parler de leurs idées pendant leur travail.
Activité 2: Addition et soustraction de fractions simples
Avant la leçon, préparez trois disques – un disque complet, un quart de disque et une moitié de disque; tous les quarts doivent être indiqués sur chaque disque (voir la Ressource 3 : Disques de fractions).
- Montrez le quart de disque et la moitié de disque et demandez à vos élèves quel serait le total si vous additionniez ces deux disques. Donnez-leur du temps pour répondre, puis quand vous obtenez la bonne réponse écrivez-la au tableau : 1/4 + 2/4 = 3/4
- Ensuite, montrez les trois disques et demandez ce que serait le total s’ils étaient tous ajoutés. Une fois de plus, attendez d’avoir la bonne réponse puis écrivez l’addition au tableau : 1 + 1/4 + 2/4 = 1 3/4
- Mettez maintenant vos élèves par deux et demandez-leur de dessiner des disques similaires en indiquant les tiers (1/3). Demandez-leur de créer des additions qu’ils doivent donner à leur partenaire ; ils doivent écrire l’addition complète et le résultat dans chaque cas.
- Pendant qu’ils travaillent, circulez dans la classe et aidez-les si nécessaire. Laissez-les essayer d’autres fractions si vous le souhaitez, pour voir s’ils comprennent vraiment l’idée.
- Affichez certaines des fractions différentes. Vous pouvez répartir cette activité sur deux leçons pour consolider l'apprentissage des élèves.
3. Utiliser le travail de groupes pour expliquer les fractions équivalentes
Comment les élèves peuvent-ils comparer des fractions ayant des dénominateurs différents (par exemple 3/5 + 1/4) ?
Ils peuvent faire des bandes de fractions pour comparer les fractions différentes, mais cette activité, bien qu’elle facilite la comparaison, ne les aide pas à additionner ou soustraire de telles fractions. Pour y parvenir, ils doivent comprendre les dénominateurs communs. La Ressource 4 :Comparaison des fractions explique leur fonctionnement.
Étude de cas 3: Utilisation du modèle partie-totalité
Mme Abdoul décide d’utiliser le modèle partie-totalité pour présenter les fractions équivalentes à sa classe et pour développer ses propres aptitudes d’utilisation du travail de groupe et du travail pratique.
Elle sait que l’utilisation d’objets de tous les jours aide les élèves à comprendre les concepts et apporte des biscuits en classe pour l’aider à expliquer les fractions équivalentes. Elle répartit d’abord la classe en groupes de huit et annonce qu’elle va expliquer comment on peut partager 20 biscuits de manière égale entre un certain nombre d’enfants.
Ensuite, elle donne à chaque groupe un nombre de biscuits différent. Elle donne 2 biscuits à un groupe et demande aux élèves de partager ces biscuits entre 4 élèves. Ils voient que 2 divisé par 4 donne ½ biscuit à chaque élève. Elle écrit au tableau 2 divisé par 4 = 2/4 = 1/2
Elle répète ce problème avec d’autres groupes et 3 biscuits partagés entre 6 élèves.
Elle donne ensuite 4 biscuits à 8 élèves - chacun obtient un demi-biscuit.
À chaque fois, elle écrit les fractions au tableau : 2/4, 3/6, 4/8, chacune étant égale à 1/2. Elle explique aux élèves que ce sont des fractions équivalentes. Mme Abdoul était heureuse de constater la réaction de la classe après sa leçon de mathématiques en utilisant des biscuits pour expliquer les fractions équivalentes.
Activité clé : Fractions équivalentes
En utilisant des moitiés, des tiers et des quarts, écrivez cinq additions, par exemple
- (1/2 + 1/4)
- (1/3 + 1/2)
- (3/4 + 2/3)
- (2/4 + 1/3)
- (2/3 + 1/4)
Montrez comment trouver le dénominateur commun de la première addition. Demandez à des groupes de deux élèves de calculer les autres dénominateurs communs.
Montrez aux élèves comment convertir le numérateur des deux premières additions ; demandez aux élèves de faire les trois additions suivantes.
Montrez comment trouver la réponse des deux premières additions ; demandez aux élèves de faire les trois dernières additions.
Demandez à chaque groupe de deux élèves de créer et résoudre autant de problèmes que possible en dix minutes.
Après la leçon, consultez la Ressource 5 : Questions d’auto-évaluation et posez-vous des questions sur votre utilisation des activités et ressources pratiques.
Ressource 1 : Fractions
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Qu’est-ce qu’une fraction ?
Une fraction est une partie d'un tout. Il y a deux nombres dans toute fraction :
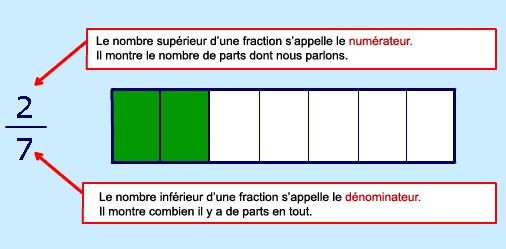
Fractions équivalentes
Les fractions équivalentes sont des fractions différentes mais qui représentent exactement la même quantité :

Vous pouvez créer des fractions équivalentes en multipliant ou divisant le numérateur et le dénominateur par le même nombre:

Ressource 2 : Bandes de fractions
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Certaines bandes de fractions sont illustrées ci-dessous. Elles peuvent être réalisées avec n’importe quel papier par pliage et ou mesure.
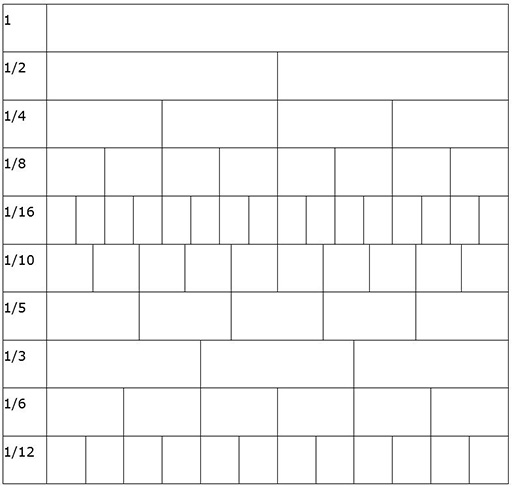
Ressource 3 : Disques de fractions
![]() Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
Ressource que les enseignants doivent planifier et adapter au niveau ou aux besoins des élèves
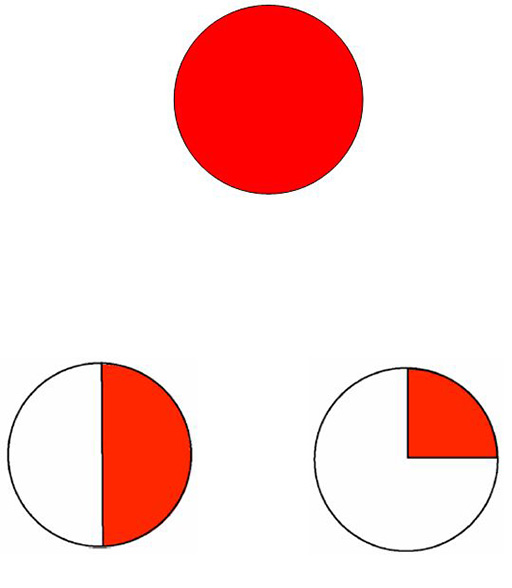
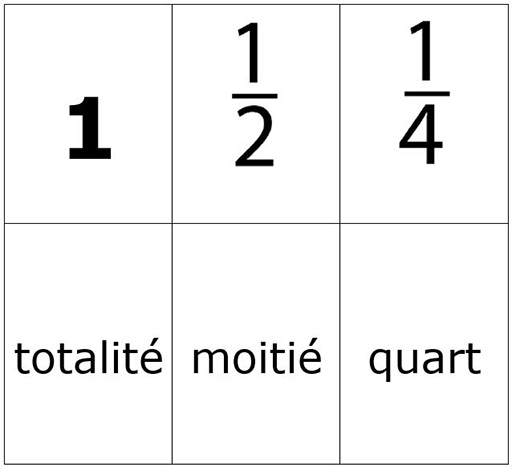
Ces disques sont réalisés en dessinant un cercle et en le divisant en moitiés, en quarts etc. en le pliant.
Ressource 4 : Comparaison des fractions
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
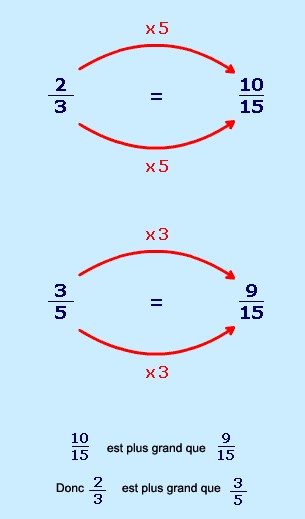
Pour comparer des fractions, vous devez d’abord les changer pour qu’elles aient le même dénominateur…
Pour comparer ![]() et
et ![]() :
:
Examinez d’abord les dénominateurs (les nombres du bas).
Trouvez un multiple commun. Un multiple commun est 15.
Changez les deux nombres en 15èmes.
Ressource 5 : Questions d’auto-évaluation
![]() Information préliminaire ou connaissance du sujet
Information préliminaire ou connaissance du sujet
Lorsque vous répondez à ces questions, vous devez absolument être réaliste. Cela vous permettra de devenir un meilleur enseignant.
- Est-ce que j’organise plus facilement des travaux en groupe ?
- Est-ce que l’utilisation de tailles et types de groupes différents a amélioré mes leçons et permis à mes élèves de mieux comprendre ?
- Est-ce que je pense que les travaux pratiques aident les élèves à comprendre, et est-ce que je les utilise facilement ?
- Mes élèves ont-ils apprécié ces activités mathématiques pratiques ?
- Est-ce que j’ai donné à mes élèves suffisamment de temps pour s'entraîner aux travaux pratiques ?
- Comment puis-je améliorer mon enseignement de ce sujet ?
- Qu’est-ce que je changerai pour la prochaine fois ?
Questions sur l’utilisation des activités pratiques et des ressources simples
- Les activités m’ont-elles aidé à atteindre mes objectifs d’apprentissage ?
- Les activités étaient-elles adaptées à ma classe ?
- Les activités ont-elles stimulé l’intérêt des élèves ?
- Les ressources m’ont-elles aidé(e) à atteindre mes objectifs d’apprentissage ?
- Les ressources étaient-elles adaptées à ma classe ?
- Les ressources ont-elles stimulé l’intérêt des élèves ?
- Les leçons étaient-elles agréables ?