Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated الثلاثاء، 10 مارس 2026، 6:33 AM
الوحدة رقم ١ :التقصّي في العدد و النمط
القسم ١ : التعلم من خلال الألعاب.
السؤال الرئيسي: كيف يمكنك استخدام الألعاب لتساعد التلاميذ على الإستمتاع بتعلم مهارات الأعداد الأساسية؟
الكلمات المفتاحية: مخطط عددي؛ الألعاب؛ التقصِّي؛ عمل المجموعة
مخرجات التعلم:
الأخ المعلم/الأخت المعلمة، بنهاية هذا القسم تكون قد:
- طورت فهمك لطرق لإستخدام الألعاب لزيادة الإهتمام و الإرتباط بالرياضيات;
- إستخدمت مجموعة من الألعاب لتساعد على تحسين الفهم الرياضي و المهارات لتلاميذك;
التمهيد
هذا القسم يستكشف طرق لإستخدام ألعاب الأرقام لتحفيز التلاميذ و مساعدتهم ليعملوا معاً. الفهم الرياضي يمكن تطويره من خلال ممارسات التعلم التعاونية.
باستخدام ألعاب بسيطة، يمكنك أن تعطي تلاميذك تطبيقات إضافية يستمتعون بها، في المجالات التي يجدون فيها صعوبة – مثلاً في المهارات الحسابية. باستخدام ألعاب ثقافية محلية ستساعدهم على التعرف على الرياضيات في الحياة اليومية.
الألعاب في هذا القسم مستخدمة بطرق مختلفة لتحفيز الإهتمام و التفكير في الأعداد
دراسة الحلقة ١:
يمكنك استخدام الألعاب لتحفيز كل التلاميذ، و ليس فقط أولئك الذين يترددون الإنشغال بالرياضيات.
يمارس الأطفال الحسابات الذهنية و مهارات أخرى أثناء استمتاعهم باللعب. باستخدام مواد بسيطة (مثلاً بطاقات، أغطية زجاج، الأحجار، إلخ) تساعد التلميذ على أن ينتبه إلى أن الرياضيات في كل مكان.
من المفروض أن تمارس دائماً كل لعبة بنفسك، قبل أن تقدمها للتلاميذ. ذلك سيؤكد أنك تفهمها و يمكنك أن تشرحها بوضوح، و بالتالي تعرف الأفكار الرياضية التي تحسنها
دراسة الحالة رقم ١:اللعب بألعاب الأعداد لتساعد الحساب الذهني
جون ، معلم الصف الثاني بمدرسة ابتدائية . وجدأن تلاميذه يستمتعون بألعاب الأرقام أثناء الفسحة. يدحرج الأولاد كرات خلال أقواس مرقمة على طاولة و البنات يرمين أكياس فاصوليا على هدف. في كل لعبة الفائز هو أول من يحصل على 20 نقطة، و لاحظ جون كيف أن بعض تلاميذه كانوا أفضل من غيرهم في جمع النقاط مع بعضها.
قرر أن يدخل ألعاباً مشابهة في تدريسه ليرى إن كان كل تلاميذه يستطيعون الجمع. قام باستخدام نفس اللعبة كل يوم مع مجموعة واحدة كل مرة لمدة أسبوع. بقية الفصل يقومون بممارسة تمارين و هو قسم وقته بين دعم أولئك الذين يلعبون و بقية الفصل. وجد أن هناك مجموعة صغيرة من التلاميذ كانوا أقل تأكداً من جمع الأعداد ذهنياً. فأعطى هؤلاء التلاميذ فرصاً إضافية ليلعبوا و خطط لهم فترات حساب ذهني أخرى.
وجد جون أيضا أن تلاميذه صاروا أكثر حرصاً على الحضور للفصل. فقرر أن تستخدم ألعابا أكثر في المستقبل.
نشاط رقم ١:إختيار ألعاب أعداد مناسبة
يجب أن تلعب هذه الألعاب بنفسك أولاً، حتى تتعرف على القوانين.
ستحتاج إلى عمل نسخ عديدة من الألعاب التي تختارها أو يمكن أن تجعل التلاميذ يساعدوك.
نظم تلاميذك في مجموعات من خمسة أو ستة تلاميذ، و أعط لعبة لكل مجموعة.
شجع المجموعات لتتحدث مع بعضها عن اللعبة و قوانينها.
كل مجموعة تختار قائداً ليؤكد أن اللعبة قد لعبت بإنصاف.
بينما التلاميذ يلعبون، تحرك حول الفصل ملاحظاً لأي فرد يواجه صعوبات حتى تخطط لطرق المساعدة فيما بعد.
في النهاية، إسأل تلاميذك:"ما الذي تعرفونه الآن لم تكونوا تعرفونه قبل بداية الدرس؟"
تساؤلات قد تحب أن تبحثها أو تناقشها مع زملائك:
هل استمتع التلاميذ بالألعاب؟ كيف تعرف أنهم استمتعوا؟
هل شارك الجميع؟ وأن لم يكن ذلك، كيف تضمن أن يكون كل فرد قد أخذ تعيينه في المشاركة ؟
هل أحسست أنك كنت على سيطرة تامة على كل الفصل؟
كيف يمكنك تحسين هذا الدرس؟ هل مجموعات أصغر تكون أفضل؟
هل أعطيت التلاميذ وقتاً كافياً لإنهاء مهماتهم؟
دراسة الحلقة ٢:
من المهم أن تلعب كل لعبة بنفسك قبل استخدامها في الفصل حتى تتأكد من أنها تستهدف إحتياجات الموضوع الذي تقوم بتدريسه.
إعتماداً على حجم فصلك و الوصول إلى الموارد، عليك أن تحدد عدد الألعاب التي تحتاج إليها. فهم مستوى الصعوبة في اللعبة مهم حتى تختار اللعبة الصحيحة للغرض الصحيح. عنصر هام آخر هو أن تترك اللعبات تُلعب في أوقات أخرى غير وقت الفصل، حيث أن ذلك سيشجع لعباً أكثر. إنشاء نادي رياضيات في مدرستك أيضاً سيشجع تلاميذاً ليلعبوا أكثرو يطوروا مهاراتهم الرياضية
دراسة حالة رقم ٢:
لعبت نوال بنقو مع تلاميذ الفصل الثاني لأنها ظنت أنها لعبة ممتازة لتساعد تلاميذها على تمييز الأعداد ذات الرقمين.
لعبت اللعبة أولاً مع كل الفصل. أعطت كل تلميذ بطاقة و بعض الأزرار. سحب تلميذ بطاقات، مرقمة من 1 إلى 50، من صندوق و قرأها على الفصل. إذا وجد تلميذ أن العدد الذي قرئ موجود ضمن كروته، وضع زراً عليه. التلاميذ الأوائل الذين تغطي أزرارهم صفاً، أو عموداً، أو قطراً صحيحاً، يفوزون باللعبة. بينما كان التلاميذ يقومون باللعب، دارت نوال حول الفصل للمساعدة. الإكمال الناجح للصف أو العمود أو القطر هو دليل على تمييزهم الأعداد من رقمين بطريقة صحيحة.
بعد ذلك قسمت الفصل إلى مجموعات من ثمانية تلاميذ و لعبوا اللعبة بسرعتهم الخاصة، متبادلين دور المنادي.
سمحت نوال للتلاميذ أن يلعبوا بنقو أثناء الفسحة، و دهشت لأعداد التلاميذ الذين انخرطوا في اللعب، خاصة في الأيام الحارة. و لاحظت أيضاً مدى زيادة ثقتهم في حصص الرياضيات.
نشاط رقم ٢:لعب بنقو للمساعدة على تمييز الأعدادالتعرف على الرياضيات في الألعاب
في هذا النشاط، أطلب من تلاميذك أن يلعبوا خمسة لعبات و يفكروا في أي رياضيات أو مهارات حسابية يظنون أنهم يتعلمونها (أنظر مورد ١: ألعاب لممارسة مهارات الحساب). قد تحتاج أن تساعدهم لتمييز الرياضيات.
أولاً، أنت تحتاج أن تلعب كل لعبة بنفسك ثم أنت أو تلاميذك . حدّد العدد المناسب من النسخ لكل مجموعة.
نظم تلاميذك في مجموعات من أربعة أو خمسة.
أعط كل مجموعة طقما من ألعاب الرياضيات الخمسة.
أطلب من كل مجموعة أن تناقش كل لعبة، وتأكد أن كل مجموعة تعرف القوانين قبل بدأ اللعب.
بعد أداء كل لعبة، أطلب من التلاميذ أن يسردوا كم من الرياضيات يعتقدون أنهم مارسوها مستخدماً الجدول في مورد ٢.
ثبت كل النتائج على الحائط حيث يمكن مناقشتها.
و أخيراً، أرسم مع تلاميذك جدولاً على السبورة لخص الرياضيات التي يعتقدون أنهم مارسوها و تعلموها.
دراسة الحلقة ٣:
ان ممارسة الألعاب المأخوذة من الثقافة المحلية هي طريقة فعالة و جيدة لتشجيع التلاميذ على الرؤية بأن الرياضيات هي نشاط شعبي، عالمي و تاريخي. هناك لعبة محبوبة جداً (مورد ٣: الألعاب الثقافية في أفريقيا) تُلعب في كل أفريقيا، لها أسماء متعددة.
هناك نسخ عديدة من هذه اللعبة. هي لعبة حسابية، تحتوي على مهارات رياضية هامة – التركيز و القدرة على التوقع – و يمكن أن يلعبها التلاميذ من مختلف الأعمار. فهْم كيفية تطويع اللعبة لإستخدام التلاميذ من الأعمار المختلفة هام للمعلم. مثلاً، في أبسط هيئاتها، هي مناسبة للتلاميذ الصغار، حيث أنها تشجع على العد و فهم مفهوم التقابل واحد لواحد. بينما عندما تتوسع اللعبة، يتعلم التلاميذ الجمع، الطرح و جمع الوحدات
دراسة حالة رقم ٣:التعرف على مهارات الأعداد مع لعبة ثقافية
الأستاذ آدم أخبر فصله عن لعبة لعبها في طفولته. أخبرهم أنهم سيلعبونها في درس الرياضيات القادم. ( أنظر مورد ٣: اللعبة الثقافية لأفريقيا )
أتى للفصل باللوحة المستخدمة و عرض اللعبة. إختار إثنين من التلاميذ أن يؤدياها و كان يشرح التحركات. أما بقية تلاميذ الفصل كانوا يسمعون و يراقبون. بعد ذلك شجعهم على طرح أسئلة.
بعد ذلك، أعطى التلاميذ موارد ليلعبوا اللعبة في أزواج (أربعة تلاميذ لكل لعبة) حيث يمكن للتلميذ مشاورة رفيقه عن التحركات. حين انتهوا، طلب منهم أن يحددوا المهارات العددية التي احتاجوا إليها لأداء هذه اللعبة.
أخيراُ، سمح للتلاميذ أن يأخذوا اللعبة إلى منازلهم و يلعبوها مع أي شخص هناك كل ليلة حتى نهاية الأسبوع.
في نهاية الأسبوع، سأل الأستاذ آدم تلاميذه عن رأي من كان بالمنزل عن اللعبة. كثيرون قالوا أن آباءهم و أجدادهم لعبوا اللعبة كما فعلوا في طفولتهم.
النشاط الأساسي: لعب لعبة أرقام ثقافية
قبل أن تبدأ، تأكد من أنك تعرف قوانين اللعبة (أنظر مورد ٣: الألعاب الثقافية في أفريقيا). إجمع عدداً كافياً من اللوحات و بذور الفاصوليا لكل مجموعة.
أقسم الفصل إلى مجموعات من أربعة و أعط كل مجموعة لوحة و عدد 48 بذرة/فاصوليا.
أطلب من كل مجموعة أن تحدد التلميذين الذَين سيلعبان اللعبة.
أترك اثنين آخرَين يلعبان.
بينما تتواصل اللعبة، تحرك حول الفصل، مساعداً عند الحاجة. إستمع إلى ما يقوله التلاميذ و سجل أي كلمات رياضية يستخدمونها.
ناقش مع التلاميذ ما سمعته، و ما رأيهم عن اللعبة.
المصدر ١: ألعاب لممارسة مهارات الحساب
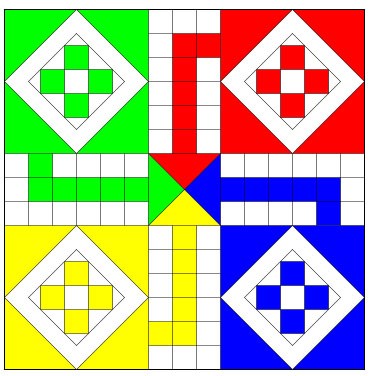
لودولوحة أطفال بسيطة لأربعة لاعبين ، حيث يسابق اللاعبون أزرارهم الأربعة من البداية حتى النهاية حسب عدد النقاط التى تظهر على ظاهر الزهر .
يتبادل اللاعبون الدور في رمي الزهر و يحركون أزرارهم حول اللوحة. حين يكون عدد النقاط على ظاهر الزهر6 يكون له الخيار أن يبدأ تحريك زر جديد حول اللوحة. إذا وصل زر إلى مكان فيه زر للاعب آخر، فعلى ذلك اللاعب أن يبعد زره و ينتظر حتى يظهر 6 ليبدأ مرة أخرى. الفائز هو اللاعب الأول الذي يوصل أزراره الأربعة إلى مركز اللوحة على المساحة الملونة بلون زره
السلم و الثعبان
يتبادل اللاعبون الدور لرمي الزهر و يحركون أزرارهم حول اللوحة. إذا هبطوا على سلم يصعدون إلى المربع الذي فيه أعلى السلم. إذا هبطوا على رأس ثعبان فيهبطون إلى المربع حيث ذيل الثعبان

بنقو
هي لعبة صدفة، حيث أن أعداداً تم اختيارها عشوائياً رسمت على بطاقة بنقو و هي تحتوي على مربعات بعضها فارغ (المثال أدناه). شخص واحد "المنادي" يكتب الأعداد من1
–100
على كرات صغيرة ثم يختارها بدون النظر ثم ينادي بالعدد. إذا استطاع اللاعبون أن يشابهوا ذلك العدد عندهم فيغطونه في بطاقتهم بفيشة، أو يشطبوه. الشئ المهم للمنادين هو أن يتذكروا أن يبعدوا الأعداد التي نادوها بعيداً، حيث سيحتاجون إليها لاحقاً للمراجعة. المنادي يختار ثم ينادي حتى يغطي أحد اللاعبين كل بطاقته ثم ينادي "بنقو!". يحتاج المنادي أن يراجع أن بطاقاتهم صحيحة ثم يعلن الفائز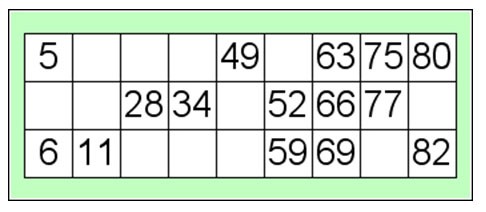
لعبة بطاقة الحلقة
"لعبات بطاقة" الحلقة" توقف التلاميذ على "أطراف أصابع أرجلهم" و تجعلهم حضوراً، حيث أنهم جميعاً مشتركون و لا يعلمون متى ستظهر بطاقتهم.

لعبة عدد المثلث
لعبة عدد المثلث هي أكثرألعاب الرياضيات تعدداً للإستعمالات لأطفال مرحلة الأساس. تلعب اللعبة بطريقة أكثر ما تشبه لعب الدومينو. جنبان من المثلث توضعان معاً حسب القانون الذي تم اختياره. بالنسبة للتلاميذ الكبار الفائز هو الذي يكمل بطاقاته أولاً، و لكن الأطفال الأصغر عادة يلعبون متعاونين. البطاقات ترتب حسب معيار سبق ترتيبه. أفضل ما
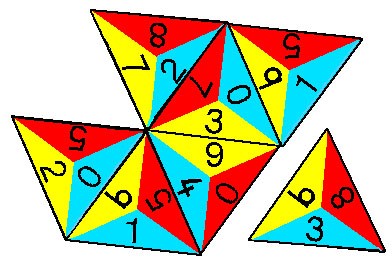
2
-4لاعبين
بعض هذه الأمثلة تم تكييفها من موقع
إذا استطعت أن تزور الموقع لتأخذ أفكاراً أخرى و أمثلة.
المصدر ٢: جدول لتسجيل مهارات الحساب
ضع علامة على كل لعبة تمت ممارستها، مثلاً اللعبة1
تساعد على الجمع.| ٥ لعبة | ٤ لعبة | ٣ لعبة | ٢ لعبة | ١ لعبة | |
| الجمع | |||||
| روابط الأعداد | |||||
| الضرب | |||||
| التركيز | |||||
| القسمة | |||||
| تشكيل مجموعة | |||||
| الدقة | |||||
| العمل الذهني | |||||
| حساب وحدات | |||||
| الطرح |
المصدر ٣: اللعبة الثقافية لأفريقيا
هذه اللعبة لها أسماء كثيرة، مثلاً:
- كوبو عند شعب فيا في سيراليون و ليبيريا
- قيوثي عند اللوو في كيني
- أُمويسو عند الغاندا في يوغندا
- بو بالسواحيلي في شرق أفريقيا
- قامباتا في أثيوبيا.
- آيو باليوربا في نيجيريا .
- أزيقو/أٌوكوي بالإقبو في نيجيريا
- واري بالأسانتي في غانا

الألواح للعب هذه اللعبة مصنوعة من، إما خشب منحوت جميل، أو برونز (في البلاط الملكي في بنين و نيجيريا)، أو ذهب (عند ملوك الأسانتي في غانا).
قوانين القيوثي
- أكثر المتغيرات تحدياً تلعب في لوحة بها عشرة حفر على كل جانب من الصفين.
- في البداية هناك ثمانية بذور ("أمبوثي") في كل حفرة.
- كل دور يبدأ بحفرة فيها على الأقل بذرتين.
- البذور إما أن توزع في أو عكس اتجاه عقارب الساعة في الحفر التالية في الدورة الأولى من الحركة.
- إذا سقطت آخر بذرة في حفرة ليست فارغة، فإن محتوياتها (بما فيها البذرة الأخيرة) توزع في دورة أخرى في الإتجاه المعاكس.
- إذا سقطت آخر بذرة في حفرة فارغة على جانبك، يتحرك اللاعب مرة أخرى، ما لم يكن قد وضع بذرة في حفرة فارغة أثناء هذه الدورة.
- إذا سقطت آخر بذرة في واحدة من حفرك الفارغة و أنت لعبت في حدود الخصم (أنظر إلى المثل على الصفحة الأخرى)، إذن تستولي على البذور في حفرة العدو المقابلة بما فيها البذرة التي وزعت أخيراً).
- إذا كانت هذه الحفرة تليها سلسلة غير مقطوعة من الحفر الفارغة على جانبك، إذن البذور التي في الحفر المقابلة أيضاً يستولى عليها.
- عندما تسقط آخر بذرة في حفرة فارغة في جانب الخصم، يكون الدور قد انتهى.
- اللاعب يجب أن يتحرك إذا استطاع. يجب أن يُعبر، إذا لم يستطع، و لكن يجب أن يتحرك مرة أخرى، إذا كان عنده ما يلعب به.
- ينتهي اللعب حين لا تكون هناك أي تحركات يمكن القيام بها.
- كل لاعب يكسب عدداً من النقاط مثل عدد البذور التي كسبها و التي في حفره بعد نهاية اللعبة.
- اللاعب الذي معه بذوراً أكثر هو الفائز.
مثل القيوثي
"لا يمكنك أن تسرق بقر رجل آخر بدون أن تدخل أرضه!"
القسم ٢: الانماط في الرسم البياني للرقم.
السؤال الرئيسي: كيف يمكنك استخدام التحقيق لتطوير فهم الأنماط العددية؟
الكلمات المفتاحية: مخطط عددي، النمط العددي، الضرب، التحقيق، عمل المجموعة، العمليات الأساسية
مخرجات التعلم:
الأخ المعلم/الأخت المعلمة، بنهاية هذا القسم تكون قد:
- استكشفت استراتيجيات لاستخدام المخططات العددية لتساعد التلاميذ ليفكروا بطريقة رياضية.;
- استخدمت طرقاً لتأسيس و إدارة تحقيقات باستخدام مخطط عددي;
- حسنت مهاراتك في العمل مع المجموعات.
التمهيد
هذا القسم سيساعدك على أن تستخدم المخطط العددي لتساعد التلاميذ ليحققوا في الأنماط العددية. و هو أيضاً سيساعدك على تحسين فهمك لكيف يدرك التلاميذ المفاهيم الرياضية، من خلال العمل التحقيقي أثناء العمل في مجموعات. ستكتسب خبرة في إدارة العمل التحقيقي و تنظيم المجموعات، حيث يمكن لتلاميذك أن يصوغوا تفكيرهم الخاص، يشرحوا أفكارهم لزملائهم، ينخرطوا في الحوار و يعطوا خلاصة. ستكون واثقاً من استخدام الأنماط العددية لدعم تحقيقات تلاميذك فيها.
دراسة الحلقة ١:
من المهم أن تساعد التلاميذ على أن يكتسبوا التمكن من التعامل مع الأعداد، من أجل أن يضعوا أسسا متينةً لمستقبلهم في الرياضيات. في هذا الجزء، ستتعلم كيف تستخدم أسئلة توجيهية لتقودهم ليحققوا في مخطط عددي و يبنوا خبرتهم في العمليات الأساسية للرياضيات. ومن خلال عملهم في مجموعات، سيتعلمون التعاون مع بعضهم، بينما تكتسب أنت خبرة في قيادة الفصل بهذه الطريقةدراسة الحالة رقم ١:استخدام الأسئلة التوجيهية للتشجيع على التحقيق في مخطط عددي
السيد موسى خطط ليساعد تلاميذه على تحقيق عمل أرقام مستخدماً مخطط عددي يحتوي على 100 مربع (أنظر مورد 1: مخطط عددي 100-مربع)
فأحضر نسخاً من مخطط عددي 100-مربع إلى الفصل. قام بتقسيم التلاميذ إلى مجموعات مكونة من أربعة تلاميذ، معطياً كل مجموعة نسخة من المخطط. و طلب منهم التحقيق في مخططهم، مدونين أي نمط يجدونه. وسألهم أسئلة توجيهية، تتضمن:
بالمرور خلال الصفوف، ماذا يمكن أن تقولوا عن الأعداد؟
ما الفرق بين أي عدد و الذي على يمينه؟
ما الفرق بين أي عدد و الذي تحته؟
هل يمكنكم تعريف مضاعفات 2 و مضاعفات 5 في المخطط؟
بينما كان تلاميذه يعملون، دار أستاذ موسى حول الفصل، ليتأكد من أن كل التلاميذ يشاركون و ملاحظاً أولئك الذين يجدون صعوبات في المشاركة. بعد 10 دقائق، جمع الفصل و طلب منهم أن يصوغوا القوانين للعلاقات و الأنماط التي وجدوها. ثم قام بتلخيصها على السبورة
نشاط رقم ١:استخدام مخطط عددي
قم بإعداد عدد من مخططات عددية من 100-مربع و قم بتقسيم الفصل إلى مجموعات من أربع تلاميذ.
اطلب من تلاميذك التحقيق في مخططاتهم و استنباط قوانين لما يلي:
أي عدد و الذي فوقه في نفس العمود.
أي عدد و الذي تحته في نفس العمود.
أي عدد و الذي على يمينه في نفس الصف.
أي عدد و الذي على يساره في نفس الصف.
بينما التلاميذ يعملون، قم بالتجول، ملاحظاً و مساعداً عند الحاجة. بعد 15 دقيقة، أطلب من عضو واحد من كل مجموعة أن يصف القوانين التي وجدوها، و ما إذا كان بقية الفصل يتفقون معهم و اكتبها على السبورة (أنظر إلى المورد 1: مخطط عددي 100-مربع).
أطلب من بعض التلاميذ أن يخبروك عما عرفوه الآن ولم يكن يعرفونه في بداية الدرس. سيكون هناك اختلاف بين التلاميذ و سيكون بعضهم مدهشاً.
إن الوسيلة 2: نماذج أسئلة: تعطي بعض الأمثلة من أنواع الأسئلة التي تساعدك على تقويم هذا النشاط. استخدم هذه الأسئلة. أسئلة أخرى يمكنك أن تفكر فيها بحيث تنعكس على خبرتك بعد النشاط – قد يكون من الأفضل أن تفعل ذلك مع زميل لك.
دراسة الحلقة ٢:
إن التحقيقات التي يجد فيها التلاميذ فرصاً ليبحثوا و يكتشفوا الحقائق بأنفسهم أو في مجموعات صغيرة، هي طرق فعالة لتعلم الرياضيات. فإذا طلبت من التلاميذ أن يقوموا بعمل أسئلتهم الخاصة البسيطة، ستتمكن من تحسين قدراتهم التحقيقية.دراسة حالة رقم ٢:ملأ خلايا فارغة على مخطط عددي
الأستاذة أكاسيا أرادت أن تنمي ثقة تلاميذها في تفكيرهم الرياضي. فقررت أن تستخدم ال 100-مربع مرة أخرى لتساعد تلاميذها ليحققوا طرقاً لحل معادلات بسيطة. قامت بإعداد نسخًا عديدة من مخطط عددي ال100-مربع، قسمت فصلها إلى أزواج و أعطت مخططاً لكل زوج. ذكرتهم بالقوانين التي استنبطوها للتحرك حول المخطط.
ثم وجهت الأسئلة التالية للمجموعات، ليقوموا بحلها مستخدمين مخططاتهم:
- كيف يمكنك التحرك من 10 إلى15؟ أملأ الصندوق 10 + = 15
- كيف يمكنك التحرك من 10 إلى 35؟ أملأ الصندوق 10 + = 35
ناقشت مع الفصل طرقاً ممكنة للتحرك من 10 إلى 35 على المخطط و ساعدت التلاميذ على أن يدركوا أن هناك أحياناً طرقاً عديدة للإجابة على السؤال في الرياضيات.
للحث على التفكير الاستقصائي ، وجهت سلوى تلاميذها ليقوم كل منهم بعمل عشرة أسئلة مشابهة و يتبادل كلٌّ مع زميله ليجيب عليها بمساعدة مربع العدد
نشاط رقم ٢:الجمع من المخططات العددية
قبل الدرس، قم بإعداد عدد من المخططات العددية (أنظر مورد 1: مخطط عددي ل100-مربع). قم أيضاً بعمل الأنشطة بنفسك و اكتشف كم عدد الطرق المختلفة التي يمكن بها حل كل سؤال.
- اطلب من التلاميذ أن يكوّنوا أزواجاً و أعط مخططاً لكل زوج. الآن اسألهم أن يحققوا في أسئلة مثل:
- كيف يمكنني التحرك من "21” إلى 34” في المخطط؟
- در حول الفصل، مستمعاً إلى أفكارهم و مسجلاً لملاحظاتك.
- الأزواج المختلفين قد يقوموا بإعطاء إجابات مختلفة، مثلاً: "سأتجه إلى الأسفل 1 و على طول 3” أو "سأذهب على طول 3 و لأسفل 1”. اسأل بعض الأزواج الذين لهم أجوبة مختلفة أن يشاركوا بها الفصل، حتى يروا أنه كثيراً ما يكون هناك أكثر من طريقة واحدة لحل سؤال.
بعد ذلك اسأل تلاميذك ليقوم كل منهم بعمل سؤال مشابه و يسأل زميله ليحله بطريقتين على الأقل
دراسة الحلقة ٣:
كمعلم في فصل دراسي تحقيقي، سيكون دورك هو ذلك المساعد و الميسِّر حتى يمكن لكل التلاميذ أن يكونوا متعلمين نشطين. من المهم أيضاً أن تكون قادرا على مساعدتهم لكي يجربوا إثارة عمل الاكتشافات من خلال تحقيقاتهم الخاصة.
في النشاط الرئيسي، سترى كيف يمكنك مساعدة تلاميذك ليحققوا بعض الأنماط باستخدام جدول حقائق الضرب. بالملاحظة الدقيقة للمجموعات أثناء عملها، يمكنك أن تقوّم أيّ تلميذ له القدرة على عمل مثل هذه الاكتشافات و أيّ تلميذ يحتاج إلى مساعدة أكبر منك
دراسة حالة رقم ٣: تحقيق الضرب بمخططات الأرقام
الأستاذة هدى تقوم بتدريس الصف الخامس. وقد ظلت تقود فصلها ليحققوا أنماط أرقام بسيطة من مخططات الأرقام، و يجروا عمليتي الجمع و الطرح باستخدام المخططات. وهي تعتقد أن تلاميذها سيستمتعون باكتشافات مشابهة عن الضرب. قامت بعمل مخطط كبير لحقائق الضرب ل 11، 12، 13 و 14 و15 وعرضته على الفصل. (أنظر مورد 3: مخططات أستاذه هدى للضرب)
سألت التلاميذ أن يعملوا في أزواج و يقوموا بعمل مخطط مشابه لحقائق الضرب ل 2، 3، 4، 5 و 6.
طلبت من التلاميذ أن يحققوا في الأعداد في الأعمدة، في الصفوف، على الطول و الأقطار و ما إذا رأوا أي خطوط للتناظر.بعد ذلك، سألت كل زوج أن يقارن إجاباته مع الزوج المجاور لهم، و تلك المجموعة من الأربعة مع أربعة آخرين. و قاموا معاُ بتسجيل النتائج التي اتفقوا عليها ثم قاموا بعرضها على جدار فصلهم.( انظر المصدر ٣)
النشاط الأساسي: استخدام مخطط حقائق الضرب
بناء على العمل السابق، أعط تلاميذك تحقيقاً، مستخدمين مخططات حقائق الضرب. قبل الحصة، قم بتجهيز مخطط كبير لحقائق الأعداد ل5، 6، 7، 8 و 9، تاركاً بعض المربعات فارغة. ستقوم بسؤال تلاميذك أن يجدوا الأعداد الناقصة مستخدمين معلوماتهم السابقة.
ابدأ درسك بمراجعة العمل السابق عن مخططات حقائق الأرقام.
قم بتقسيم الفصل إلى مجموعات من أربعة أو خمسة و أطلب من كل مجموعة أن تقوم بنسخ مخططك.
أطلب من تلاميذك أن يناقشوا معاًً ما هي الأعداد المفقودة ، ويكتبوها في المربعات الفارغة، ثم يثبتوا نتائجهم على الحائط. بينما هم يعملون، تجول حول الفصل مستمعاً و مساعداً – فقط حين يكون الأمر ضرورياً جداً – بإعطاء أسئلة و ليس بإعطاء أجوبة.
ما هي الحقائق التي تعرفها؟
ما هي الأعداد المفقودة؟
هل يمكنك رؤية نمط في الصف، في العمود؟
اسأل عضواً من كل مجموعة كيف توصلوا إلى إجاباتهم و قم بعمل نقاش للفصل لتقرر الإجابة الصيحة.
أخيراً، أنظر إلى الأسئلة في المصدر ٢ لتساعدك على التفكير في كيف سار الدرس
المصدر ١: مخطط عددي
المخطط العددي ل100-مربع، هو ببساطة شبكة، تحوي على 100 مربعاً ، حيث المربعات مرقمة أفقياً تبدأ من ’1’ في الركن الأعلى على الأيمن.
قد يمكنك أن تشتري سبورة طباشير كبيرة واحدة، أو تطبع نسخة من هذا المورد أو تصنع واحدة بنفسك.
هنا بعض أمثلة القوانين التي يمكن للتلاميذ، بسهولة أن يكتشفوها حين يعملون بمخطط عددي 100-مربع:
- للذهاب للأعلى درجة واحدة، اطرح 10
- للذهاب للأسفل درجة واحدة، اجمع 10
- للذهاب للأيسر درجة واحدة، اطرح 1
- للذهاب للأيمن درجة واحدة، اجمع 1
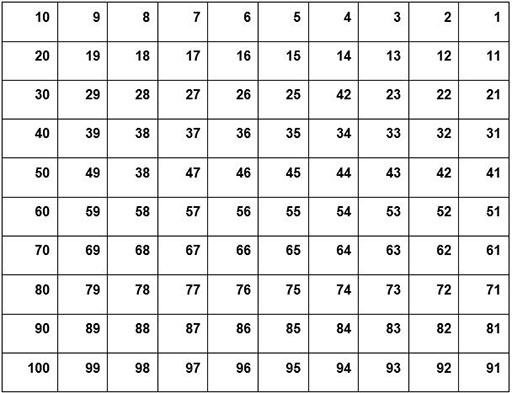
المصدر ٢: تفكير بشأن درسك:
بنهاية أي حصة، من المفيد دائماً التفكير في كيف سار الدرس. بطرح بعض الأسئلة على نفسك و الإجابة عليها بأمانة، ستفكر بعمق أكثر في دورك و مسئولياتك كمعلم.
هنا بعض الأسئلة التي تساعدك على التفكير فيما فعلته بطريقة جيدة و ما هي المجالات التي يمكنك تحسينها أكثر.
- هل قام المخطط بإرساء قاعدة جيدة للدروس المقبلة؟ كيف حدث ذلك؟
- هل استمتع التلاميذ بهذا التحقيق؟ كيف عرفت أنهم استمتعوا؟
- هل شارك كل التلاميذ؟ إذا كانت الإجابة بلا، كيف يمكنك تحقيق ذلك في المرة القادمة؟
- هل تشعر أنك كنت مسيطراً على الفصل بصورة كاملة؟
- كيف يمكنك تحسين هذا الدرس و مساعدة تلاميذك لفهم أفضل؟
- هل مجموعات أصغر ستكون أفضل؟ لماذا؟
- هل أعطيت التلاميذ وقتاً كافياً لمهماتهم؟ كيف تعرف؟ هل ستعطيهم وقتاً أطول في المرة القادمة؟
- هل أعطيت كل التلاميذ فرصة لمناقشة ماذا فعلوا؟ هل أدى ذلك إلى جعلهم يمارسون التفكير و الفهم؟
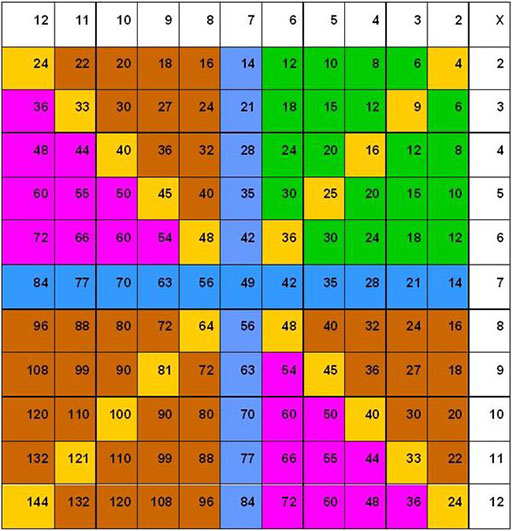
المصدر ٣: مخططات الأستاذة هدى للضرب
في مخططاتك للأعداد، ظلل مضاعفات 11، 12، 13، 14 و 15 – فكر: هل يمكنك استخدام ألوان مختلفة لتظليل مجموعات مضاعفات مختلفة، أو تستخدم مخططات مختلفة؟
قوانين مخططات الضرب
- الأعداد متماثلة حول القطر.
- الصفوف و الأعمدة تتشابه، أي أن الصف الأول مثل العمود الأول، و الصف الثاني مثل العمود الثاني، و هكذا.
- القطر الرئيسي هو خط التماثل.

مثال اخر لجداول الضرب
القسم ٣: وسائل حل المسائل الرياضية.
السؤال الرئيسي: كيف يمكنك تنمية مهارات التلاميذ في حل المسائل؟
الكلمات المفتاحية: ما بعد الإدراك؛ التمييز؛ المهام؛ الإبداع؛ ’التفكير في التفكير’
مخرجات التعلم:
الأخ المعلم/الأخت المعلمة، بنهاية هذا القسم تكون قد:
- استكشفت استراتيجيات التلاميذ في حل مسائل الرياضيات؛;
- صرت قادراً على التمييز بين الصفات العميقة و السطحية للمسائل الرياضية؛;
- صرت ماهراً في التقنيات التربوية لتنمية فهم ما بعدالإدراك عند التلاميذ..
التمهيد
هذا القسم سيساعدك على تطوير استراتيجيات تشجع التلاميذ على أن يكون لهم تفكير رياضي واضح، يستطيعون حل المسائل الرياضية و يفهمون و يميزون الميزات العميقة للمسائل الرياضية. قبل أن تبدأ هذا القسم، من المفيد أن تفكر في اهمية حل المسائل. بعض الأسباب موجودة في المصدر1: لماذا يعتبر حل المسائل مهمادراسة الحلقة ١:
"التفكير في التفكير"، أوما بعدالإدراك ، هو وسيلة قوية لمساعدة التلاميذ على فهم و تمييز الميزات "العميقة" لأنواع معينة من المسائل’ و كيف تحل هذه المسائل.
فالخطوة الأولى نحو هذا التفكير هي أن تنشئ فرصاً للتلاميذ ليتحدثوا عن المسائل التي يحاولون حلها. من المهم الأ تصدر أحكاماً عندما يكون التلاميذ شارعين في شرح أفكارهم علناً.
هناك طرق مختلفة عديدة لحل المسائل الرياضية (أنظرإلى المورد 1). قد تندهش لعدد الطرق الأخرى التي يجدها التلاميذ، غير الطريقة التي توقعتهم أن يستعملوها.
دراسة الحالة رقم ١:الإستماع لأصوات التلاميذ في الرياضيات
ذكّرت هنادي تلاميذها أنهم، حين يعودون إلى بيوتهم من المدرسة، ليس هناك فقط طريق واحد للوصول للبيت: هناك طرق عديدة ممكنة. بعضها أقصر، بعضها أطول، بعضها أكثر أماناً، بعضها أكثر تشويقاً. أخبرتهم أن مسائل الرياضيات مثل ذلك - هناك عادة أكثر من طريقة واحدة لإيجاد الإجابة الصحيحة، و النظر إلى الطرق المختلفة قد يكون مشوقاً.
كتبت هنادي الأسئلة التالية على السبورة:
-طارق عنده 24 جنيه و هو ينفق 9 جنيه على الشيكولاته. كم يتبقي له؟
تأكل ندى 7 قطع من الحلوى كل يوم. وعندها 42 قطعة حتى كم يوماً ستكون عندها حلوى؟
اشترت المعلمة نجاة 25 صندوقاً من الألون و بكل صندوق 12 لوناً. كم لوناً يكون عندها؟
بعد ذلك، سألت التلاميذ ليجيبوا على الأسئلة مستخدمين الطريقة التي يفضلونها. أعطت تلاميذها عشرة دقائق للإجابة على الأسئلة. ثم طلبت منهم أن يتناقشوا فيما بينهم في كيفية إجاباتهم على كل سؤال.
أخيراً، مرت على كل سؤال مع الفصل، طالبة من ثلاث تلاميذ أن يحضروا إلى المقدمة و يشرحوا للفصل كيف توصلوا للإجابة على كل الأسئلة.
قامت بعمل قائمة بالطرق التي استخدموها لإيجاد الإجابات و كتبت قائمة بالطرق التي استخدمها معظم التلاميذ
نشاط رقم ١:إعطاء مكانة للطريقة التي يفكر بها الأطفال
من الأفضل أن تحاول هذا النشاط مع اثنين أو أكثر من الزملاء أولاً، ثم حاوله مع التلاميذ بعد ذلك:
- اسأل تلاميذك أن يحاولوا هذه الأسئلة الثلاثة بالعمل منفردين.
- طارق عنده 24 جنيه و هو ينفق 9 جنيه على الشيكولاته. كم يتبقى له؟
- تأكل ندى 7 قطع .من الحلوى كل يوم. وعندها 42 قطعة حتى كم يوم ستكون عندها حلوى؟
- إشترت المعلمة نجاة 25 صندوقاً من الألوان. في كل صندوق 12 قلما ملونا. كم قلما ملونا. عندها؟
- اقسم الفصل إلى مجموعات من أربع أو خمس تلاميذ. أطلب منهم أن يأخذ كلٌّ منهم دوره ليوضح لبقية زملائه بدقة كيف توصلوا لإجاباتهم.
- بعد ذلك، أطلب من المجموعات أن توضح كيف حلت المسائل، ثم وجه هذه الأسئلة:
- هل حصلتم جميعاً على نفس الإجابة؟
- هل حللتموها جميعاً بنفس الطريقة
- كم عدد الطرق التي يمكن لمجموعتكم أن تجدها لتصل إلى الحل الصحيح لكل سؤال؟
- اكتبها في قائمة على السبورة
وضح كيف أنه من المهم لتلاميذك أن يحلوا المسائل و ينموا تفكيرهم الرياضي
دراسة الحلقة ٢:
أي مهمة أو مسألة رياضية تطرحها على تلاميذك، تتطلب ، سمات "عميقة" – تعرف السمات التي تحدد طبيعة المهمة، و كذلك الإستراتيجيات التي يمكن أن تساعد في حلها.
أكثر المسائل الرياضية لها سمات عميقة، مغطاة بمجموعة معينة من السمات الظاهرية. كمعلم، عليك أن تساعد تلاميذك أن يفهموا أنهم بمجرد أن عرفوا السمات الظاهرية، تغييرها ليس له أي أثر على كيفية حل المسألة. فإن إستراتيجيات الحل تظل كما هي. (أنظر المورد ٢: طرق لمساعدة التلاميذ في حل المسائل)
دراسة حالة رقم ٢:جوهر المسألة
كتب ادوارد الأمير هذه المسألة في السبورة.
"في عائلة واحدة، هناك طفلان: نزارعمره 8 سنوات و مازن 4 سنوات.
ما هو متوسط أعمار الطفلين؟"
أراد بعض التلاميذ الإجابة فوراً على السؤال، و لكن ادوارد أخبرهم أنه يريدهم قبل أن يأتوا بالإجابة ، أن ينظروا بتمعن في السؤال – أي نوع من الأسئلة هي. هل هناك أي شيء يمكنه تغييره دون أن يغير ذلك المجموع؟
وجد بعض التلاميذ أنه يمكنهم أن يغيروا أسماء الأطفال دون أن يغير ذلك المجموع. فهنأهم الأستاذ.
كتبت في السبورة جمعاً بسيطاً (1+1=2) ثم قال،’إذا غيرت الأعداد هنا (كتب: 2+5=7) ثم قال،"إنه ليس نفس المجموع و لكنه نفس النوع من الجمع”.
اقترح بعض التلاميذ أنهم يمكن أن يغيروا أعمار التلاميذ بالإضافة إلى الأسماء.
ثم سأل ادوارد:"هل سيكون هناك نوع مختلف من الجمع إذا تحدثنا عن بقر بدلاً من أطفال؟"
واصلوا الدرس بهذه الطريقة، حتى أدركوا أنهم يمكن أن يغيروا الشيء المعتبر، العدد و ملكية تلك الأشياء المحسوبة، كل ذلك بدون تغيير نوع الجمع المنفذ.
بعد ذلك، بدأ التلاميذ الكتابة والإجابة على عدد كبير من الأمثلة من هذا النوع من الجمع، أكثر مما كانوا ا يتخيلونه.
نشاط رقم ٢:ما الذي يمكن أن يتغير؟ ما الذي يجب أن يبقى كما هو؟
حاول النشاط بنفسك أولاً
- أكتب السؤال التالي في السبورة: 10 أشخاص توافدوا إلى حفلة و كل شخص يصافح بيده كل شخص آخر مرة واحدة. كم عدد المصافحات التي تمت في تلك الحفلة؟
- اطلب من تلاميذك في مجموعات من أربعة أو خمسة، أن يناقشوا معاً ما الذي يمكن تغييره في السؤال، بينما يتركونه جوهرياً بدون تغيير بحيث يمكن حله بنفس الطريقة.
أطلب من المجموعات أن تجد معاً مثالاً آخر، له نفس الجانب جوهرياً ، حيث أن المهمة الأساسية لا تتغير. حل المسائل، ثم وضح لكل الفصل، الإستراتيجية أو الإستراتيجيات التي اتبعت
دراسة الحلقة ٣:
الحاجات إلى حل الأسئلة يجب أن تكيف لكل تلميذ، بحيث يمكنه المشاركة. مثلاً، كل التلاميذ يمكنهم المشاركة في ما الذي يجعل المسألة سهلة أو صعبة الحل. قد تكون الاختلافات في السمات الظاهرية – مثلاً، استخدام أعداد أكبر، علامات عشرية أو كسور، بدلاً من أعداد صحيحة صغيرة – التي عادة ما تجعل المهمة صعبة للحل.
أحياناً، وضع سؤال في سياق معين قد يجعله أسهل. ولكن ذلك يمكن أن يلفت نظر التلاميذ عن السمات العميقة للمسألة، حيث أنهم قد لا يستطيعون النظر بسهولة إلى الطريقة المراد استعمالها
حين يفهم التلاميذ السمات العميقة للمسألة، سيمكنهم ذلك استكشاف أي سمات ظاهرية، يفهمونها و ينظرون من "خلالها"، حيث يميزون المهمة الجوهرية . كل التلاميذ حينذاك، يمكنهم أن يعالجوا أي مهمة مثلها بثقة و بسهولة. (أنظر إلى المصدر٢) عوامل هامة لك لوضع وحل مسائل مع تلاميذك.
دراسة حالة رقم ٣:اجعله سهلاً، اجعله صعباً
كانت ماري تعمل مع تلاميذها في موضوع القسمة.
كتبت ثلاثة مسائل على السبورة:
جون عنده 12 برتقالة، و3 أطفال. إذا قسم البرتقال بالتساوي بينهم، كم برتقالة يأخذها كل طفل؟
أقسم 117 على 3
شومي عندها 94 جنيه للذهاب إلى مكان عملها. هي تصرف 15 جنيه كل يوم للتاكسي. في أحد الأيام، لم يكن عندها ما يكفي للتاكسي. لمدة كم يوم ذهبت للعمل؟ في اليوم الذي لم تتمكن من الذهاب للعمل فيه كم جنيهاً إضافيا تحتاجه للتاكسي لتتمكن من الذهاب للعمل؟
سألت التلاميذ في مجموعات من أربعة تلاميذ، أن يحاولوا حل هذه المسائل معاً.
بعد عشرة دقائق، سألت ماري تلاميذها أي المسائل كان حلها أسهل أو أصعب من غيرها. و معاً قاموا بعمل قائمتين على السبورة -"الأشياء التي تجعل المسائل صعبة" ، و "الأشياء التي تجعل المسائل سهلة”.
سألت مارى المجموعات أن يبحثوا عن كم هي الطرق المختلفة التي يمكنهم بها حل المسائل التي أعطيت لهم. و قالت أنها ستكافئ المجموعة التي ستجد العدد الأكبر من الطرق، و ذلك بعرض شهادة "أبطال الرياضيات" مع أسمائهم عليها على جدار الفصل
النشاط الأساسي: تلاميذ يكتبون مهامهم بأنفسهم
- مستخدمين القائمتين على السبورة -"الأشياء التي تجعل المسائل صعبة" و "الأشياء التي تجعل المسائل أسهل"، أطلب من تلاميذك في مجموعاتهم أن يكتبوا ثلاثة أسئلة. بحيث يكون سؤالا واحدا سهلاً، و سؤالا صعباً و واحد معقداً.
- بعد عشرة دقائق، أطلب من المجموعات أن تتبادل أسئلتها التي كتبتها مع مجموعة أخرى، و كل مجموعة تحل الأسئلة التي استلمتها من المجموعة الأخرى.
- أطلب من المجموعات أن تتجمع لتعطي تقرير عن الطرق. ناقش هذه الطرق المختلفة التي سلكها التلاميذ ليصلوا إلى الإجابة. أطلب منهم أن يحاولوا طرقاً أخرى للحل.
كيف ساعد هذا النشاط تلاميذك أن يكونوا أكثر ثقة في حل المسائل الرياضية؟
المصدر ١: لماذا حل المسائل شيء مهم
حل المسائل:
- يزيد الاستمتاع و التشويق لدروس الرياضيات؛
- يساعد التلاميذ أن يكتسبوا ثقة في قدراتهم الرياضية؛
- يساعد التلاميذ أن يروا التفاعل بين الرياضيات و حياتهم اليومية؛
- يساعد التلاميذ أن يثمنوا تعلم الرياضيات؛
- ينمي مهارات الاتصال في الرياضيات؛
- يطور فرضيات عملية التشكيل و الاختبار؛
- ينمي التفكير المجرد و المنطقي.
استراتيجيات لحل المسائل
- ارسم صورة أو شكل.
- اعمل جدول.
- اعمل قائمة.
- ابحث عن نمط.
- اختر ترقيماً.
- خمن و راجع.
- اعد صياغة المسألة.
- انظر إلى كل الاحتمالات بشكل منظم.
- اشتغل عكسياً.
- حل مسألة بسيطة بها متغيرات أقل.
- حلل المسألة ثم اشتغل فيها مرحلة بمرحلة.
- استكشف دور كل متغير بالتبادل مع تثبيت المتغيرات الأخرى.
- استكشف أي مسائل سابقة بتشكيل معطيات و نتائج مشابهة.
- دقق في الفرضيات المخفية.
القسم ٤ : رؤية عملية الضرب.
السؤال الرئيسي: كيف يمكن للتحقيقات العملية التي تتعلق بالأشكال و الأنماط البصرية أن تساعد التلميذ على فهم الضرب؟
الكلمات المفتاحية: التصور؛ الضرب؛ الشكل؛ الخيال؛ التتابع؛ التخطيط؛ عمل المجموعة
مخرجات التعلم:
الأخ المعلم/الأخت المعلمة، بنهاية هذا القسم تكون قد:
- خططت، أعددت و قمت بعمل درس يشجع التلاميذ على استكشاف الضرب من خلال الوسائل البصرية ووصلت للسبل التي تمكنك من عمل الشئ الجديد المبتكر.;
التمهيد
هذا القسم يستكشف كيف يمكنك تخطيط التحقيقات و إجراء لعملي، بحيث يمكن استخدام الأعداد و الأنماط الهندسية كوسائل لمساعدة التلاميذ على تنمية فهمهم للضرب (مدخل مشابه يمكن محاولته مع القسمة). كذلك ستكستكشف الضرب من خلال تمييز النمط.دراسة الحلقة ١:
هدفك في هذا القسم، هو أن تطور فهم التلاميذ للأعداد المربعة من خلال عمليات التساؤل و النشاط اليدوي، باستخدام بطاقات لعمل أشكال مربعة. كم عدد البطاقات التي يمكن استخدامها لعمل أشكال مربعة (تلك التي يتساوى فيها عدد البطاقات في الصفوف وفي الأعمدة؟)
تحتاج أن تخطط الدروس للتأكد من أن كل التلاميذ مشاركون في النشاط. في النشاط ١، ستطلب من تلاميذك أن يعملوا في أزواج.
دراسة الحالة رقم ١:ترك التلاميذ أن يعملوا مع الحد الأدنى من التوجيه
أرادت نور من تلاميذها أن يعملوا بعض التحقيقات في أزواج، بتوجيه منها فقط. كانت حريصة على أن ترى إن كان التلاميذ يمكنهم التحقيق في الأعداد المربعة بأنفسهم.
بدأت الدرس بالطلب من التلاميذ أن يعملوا في أزواج. رسمت 4 علامات ضرب (×)على السبورة في شكل مربع ثم طلبت من التلاميذ أن يستخدموا 9 علامات ضرب بنفس الطريقة لعمل مربع آخر. ثم طلبت من الأزواج أن يرسموا أكبر عدد ممكن من المربعات الأخرى بنفس الطريقة في خمس دقائق. بعد الخمس دقائق، طلبت من بعض التلاميذ أن يخرجوا و يرسموا بعض مربعاتهم في السبورة و يكتبوا كم علامة ضرب في كل واحد. أخبرت التلاميذ أن تلك الأعداد تسمى "الأعداد المربعة”.
سألت نور التلاميذ إن كان يمكنهم عمل أعداد مربعة أكثر، و أن يكتبوا عدد علامات الضرب المطلوبة لعمل كل مربع – (العدد المربع) في الخمسة دقائق التالية، رسم الأزواج بعض الأعداد المربعة مستخدمين علامات الضرب. مرة أخرى، قام بعض التلاميذ برسمها على السبورة و عد علامات الضرب.
بترك التلاميذ يعملون بغير توجيه بشكل رئيسي، أحست نور بأنهم يكتسبون ثقة في قدرتهم على العمل في مادة الرياضيات و كذلك يجدون متعة في الدرس. وجدت أيضا أن معظم الأزواج عملوا جيداً مع بعضهم
نشاط رقم ١:رسم الأعداد المستطيلة المربعة
أنظر إلى المهمة في المورد ١: الأعداد المربعة. ستشجع كل تلميذ في مجموعته الزوجية، أن يشارك وذلك بتفويض مسؤولاعلى الرسم و الآخر على تسجيل العدد. ر ، ومن ثم يتبادلا هذه المهام. بهذه الطريقة ستتأكد من أن كل التلاميذ سيشاركون.
مستخدماً أجساماً (بذور أو أحجار صغيرة) كبطاقات، أو بكتابة علامات ضرب على ورق أو لوحة، خطط و أجر حلقة تعلم حيث يحاول كل الأزواج من التلاميذ أن يجدوا "أعداداً مربعة" (تلك التي بها عدد متساوي من البطاقات في كل صف، وفي كل عمود).
ما الخصوصية في "الأعداد المربعة"؟
دراسة الحلقة ٢:
في هذا الجزء، سنتخلى عن الحاجة " للمربعات"، حيث هناك عدد متساوي من الصفوف و الأعمدة. المتطلب الوحيد الآن هو أن كل صف في الشكل يجب أن يتم عمله من نفس العدد من علامات الضرب أو البطاقات: عدد الصفوف و الأعمدة يمكن أن يختلف. ذلك يدل على أعداد "المستطيل”. هل تتوقع أن يكون هناك أعداد "مستطيل" أكثر أو أقل من "أعداد مربع"، و هل يمكنك أن تفسر لماذا؟ مستخدماً أسئلة مفتوحة النهايات تجعل التلاميذ يفكرون بشكل أوسع في المهمة.
إن النظر إلى الأعداد التي تكون أشكال المستطيل هي طريقة واحدة للتلاميذ ليستكشفوا الضرب (أو القسمة) من خلال النظر و العمل، بالإضافة إلى الحساب العقلي و المكتوب. حاول التحقيقات بنفسك، لترى أين يمكن للتلاميذ أن يجدوا صعوبات ثم خطط كيف يمكنك مساعدة هؤلاء.
دراسة حالة رقم ٢:ممارسة ألعاب لإيجاد عوامل
خططت الأستاذة أتشان لتطلب من تلاميذها أن يجدوا أعداد مستطيل مختلفة باستخدام حقائق الضرب. قررت أن تعمل منافسة في الفصل بتقسيم الفصل إلى فريقين. كل فريق يجب أن يختار مراقب نتيجة. تتمثل اللعبة في كتابة عدداً على السبورة، و أول تلميذ يستطيع أن يعطيها عاملين صحيحين لذلك العدد، سيكسب نقطة لفريقه. الأستاذة أتشان، أوضحت أن هناك أكثر من إجابة صحيحة واحدة – أحياناً تكون إجابات كثيرة. بعد ذلك عرضت للفصل مثالاً بكتابة العدد 6 و أخبرتهم بأنها ستعطي نقطة لكل تلميذ قال ”2 في 3” أو ”3 في 2” أو ”1 في 6” أو ”6 في 1”. استمتع التلاميذ باللعبة و صاروا في غاية الحماس. كانت الأستاذة أتشان في غاية الفرح، و خططت مسبقاً أن هذه اللعبة ستساعد تلاميذها في نشاطهم التالي.
في مهماتها التالية، كثيراً ما قامت بهذه اللعبة عندما تكون هناك خمسة دقائق بقيت في نهاية الحصة.
نشاط رقم ٢: الضرب باستخدام البطاقات
ستحتاج إلى 20 بطاقة، أغطية قارورات زجاج، حبوب فاصوليا أو أحجار، لكل مجموعة من أربع أو خمس تلاميذ.
ابدأ بتقسيم الفصل إلى مجموعات و إعطاء البطاقات.
انسخ أو ارسم الجدول الموجود في المورد ٢: جدول الضرب، على السبورة. أطلب من كل تلميذ أن ينسخه، ليسجلوا فيه ما يجدونه.
أطلب من المجموعات أن تأخذ 6 بطاقات و يرتبونها في صفوف من أعداد متساوية باستكشاف كل الترتيبات الممكنة التي يستطيعون عملها.
بعد خمسة دقائق، أترك المجموعات تتشارك الترتيبات الممكنة التي وجدوها للعدد 6. راجع أن هناك على الأقل مجموعة واحدة قد ضمّنت ترتيباً بصف واحد فقط. أطلب منهم أن يملئوا جدولهم ل 6 كما هو في المورد ١.
بعد ذلك، أجعلهم يحاولون العدد 12 و لكن، قبل أن ينفذوا الترتيبات، يجب أن يتوقعوا عدد الترتيبات الممكنة، ثم يتأكدون إن كانت توقعاتهم صحيحة.
كرر ذلك مع كل الأعداد التي هي في الجدول
دراسة الحلقة ٣:
الآن، المطلوب منك أن تفكر في طريقة أخرى للنظر إلى النمط في الضرب، بحيث لا ترتكز على الأشكال و البطاقات، و لكن أيضا باستخدام الأنماط في الصفوف والأعمدة. إن مساعدة التلاميذ على استكشاف أنماط خلال أنشطة عملية، سيزيد اهتمامهم بالرياضيات أكثر و يطور تفكيرهم الأعمق. تخيل عمودين، واحد "للعشرات" و آخر "للآحاد”. إذا فكرنا، مثلاً في جدول 8، الأربعة أعداد الأولى هي:
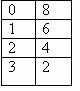
يمكنك استخدام مثل هذه الملاحظات و الأسئلة لتساعد التلاميذ أن يتعلموا كلاً من الضرب و تمييز الأنماط
دراسة حالة رقم ٣: تمييز الأنماط في الضرب
أراد الأستاذ كوكو أن يقوم بنشاط يستكشف فيه الضرب في 9. و قرر أنه، بالرغم من أن تلاميذه معتادون على أعداد المربع و المستطيل، فقد احتاجوا أولاً إلى ممارسة تمييز أنماط بسيطة أخرى. كانوا قد قاموا بعمل مشابه في سنة سابقة، ولذا كان بعض تمييز هذه الأنماط معاداً.
طلب منهم في أزواج أن يملئوا الأعداد المفقودة التالية:
1) 4، 6، 8،.....، 12، 14
2) 3، 6، ....، 12، 15
3) 16، 25،.......، 49، 64
4) 1، 11، 111، ...، 11111
5) 1، 1، 2، 3، .....، 8، 13
عندما انتهى التلاميذ و تمت مناقشة الإجابات، طلب من الفصل أن يعملوا أنماطهم الخاصة و يتركوا فيها عدداً مفقوداً. بعد ذلك تبادلوا أنماطهم مع رفقائهم و ملئوا الأعداد الناقصة.
بعد ذلك، طلب منهم عمل نمطا مستخدمين العدد 9.
بدأ التمرين ثم طلب منهم المتابعة 0، 9، 18، 27، 36، ، ، .....
كانوا في غاية الحماس و الاستمتاع بالنشاط الذي طلبه منهم الأستاذ كوكو. ثم سألهم إن استطاعوا رؤية أي نمط؟ و هل يمكنهم توقع العدد الأخير و كل إجابة؟ كان مبتهجاً لأن بعضهم استطاع القيام بذلك.
عادة ما يستخدم الأستاذ كوكو العمل في أزواج، وهكذا جعل كل واحد يشارك و يتكلم مما ساعد في تطوير تفكيرهم
النشاط الأساسي: استكشاف مضاعفات
ستحتاج إلى المورد ٣: جدول مضاعفات 9
قف بجانب السبورة و اطلب من التلاميذ أن يصمتوا تماماً. اطلب منهم أن يراقبوا بعناية.
اكتب الخمسة ضربات الأولى في 9 على السبورة.
تمهل قليلاً. أطلب منهم أن ينظروا إلى ما يحدث للأعداد.
اطلب من أحد التلاميذ أن يكمل النمط حتى 10×9.
اطلب من الفصل أن يشاركوا بأي شيء يلاحظونه، و قم بتسجيل كل شيء بدون تعليق.
واصل، و لكن قف بعد 13×9، أترك مسافة ثم أكتب 17× 9 = ؟ الآن، راقب بعناية بينما هم يحاولون فهم ما يجري. حتى الآن لا تتدخل، و لكن اجعلهم يتعجبون من طلاقتك في الضرب في 9.
أسأل إن كان التلاميذ يلاحظون أي شيء آخر مثير في النمط.
أخيراً، اسأل: “ما هي الإجابة علىْ 17×9؟
كيف كان تفاعل تلاميذك مع هذه الطريقة في العمل؟ ما الذي تعلموه
المصدر ١: إعداد المربع
يجب أولاً أن ترسم مربعاً على السبورة معرفاً الجوانب ب 2 سم و أقسمه كما هو موضح إلى مربعات 1 سم.

المسجل الأول، عليه أن يحسب مربعات ال 1 سم ثم يكتب الكاتب العدد.
الآن، الكاتب، عليه أن يرسم مربع 3 سم و يقسمه بنفس الطريقة إلى مربعات 1 سم و المسجل يحسب و يسجل هذه المربعات الصغيرة.
يستمر النشاط مع مربعات 4 سم، 5 سم و 6 سم.
أمثلة
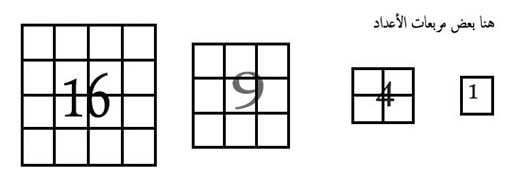
بعد ذلك يطلب منهم أن يرسموا مستطيلين: 3 سم × 2سم و 4 سم × 5سم. يتبادلون الأزواج الدور ليرسموا/يسجلوا الأعداد. بعد وقت قصير، اطلب منهم أن يتوقفوا و يعرضوا أيها أعداد مربع، أي أن بها نفس العدد أفقياً و إلى تحت. أطلب منهم أن يدرجوا أعداد المربع حتى إلى مائة.
المصدر ٢: جدول الضرب
| عدد الترتيبات | الترتيبات الممكنة | العدد |
| 3 | ||
| 4 | ||
| 4 | (1×6) (2×3) (3×2) (6×1) | 6 |
| 8 | ||
| 9 | ||
| 10 | ||
| 12 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 18 | ||
| 20 |
المصدر ٣: جدول مضاعفات (مثلاً جدول مضاعفات 9)
1×9 = 9
2×9 = 18
3×9 = 27
4×9 = 36
5×9 = 45
6×9 = 54
7×9 = 63
8×9 = 72
9×9 = 81
10×9 = 90
11×9 = 99
12×9 = 108
13×9 = 117
14×9 = 126
.17×9 = ؟
إننا نلاحظ بالآحاد تنقص بواحد كل مرة تنزل إلى تحت بينما العشرات تزداد بواحد، ما عدا بين 10× و 11×
هناك ملاحظة أخرى وهي أن عندما تجمع الأرقام في المجموع، يصير مجموعها 9.
القسم ٥ : عمل عملي باستخدام أشرطة و أقراص الكسور.
السؤال الرئيسي: كيف يمكنك استعمال أشرطة وأقراص الكسور لتنمي فهم التلاميذ للعمل بالكسور؟
الكلمات المفتاحية: أشرط الكسور؛ أقراص الكسور؛ العمليات البسيطة؛ عمل المجموعة
مخرجات التعلم:
الأخ المعلم/الأخت المعلمة، بنهاية هذا القسم تكون قد:
- طورت فهمك و مهاراتك في استخدام نشاطات العملية و الموارد البسيطة.;
- صرت قادراً على مساعدة فهم التلاميذ للكسور مستخدماً موارد بسيطة.;
- صرت واثقاً من استخدام عمل المجموعات و حل المسائل لتنمية ثقة التلاميذ بالتعامل مع الكسور..
التمهيد
استخدام مفهوم أجزاء-من-الكل لإستكشاف الكسور يقدم لك سياقاً مناسباً لتطوير فهمك لأهمية الأنشطة العملية و استعمال الموارد.
إن إعطاء الفرصة للتلاميذ لتقسيم الاشياء إلى أجزاء-من-الكل، مستخدمين أجساماً حقيقية، سيساعدهم على استيعاب الأفكار المجردة. ستستعمل موارد مختلفة و أنشطة عملية، و تنظم تلاميذك بطرق مختلفة لترى أي طرق التجميع تعمل بطريقة افضل بالنسبة لوضعك. أنت أيضاً مشجََّع، لإستخدام عمل المجموعات مستعملاً منها مختلف الأحجام و الأنواع. مرة أخرى، أنت ستقرر ما إذا كان نوع واحد أفضل من آخر لمهمة محددة.
دراسة الحلقة ١:
في هذا القسم، ستحقِّق في ميزات استخدام عمل المجموعات و مهام عملية لتقدم مفهوم الكسور. بمحاولة إستعمال مهام و أنشطة مع مجموعات من أحجام مختلفة، ستكون قادراً على اعتبار ما هو أكثر مناسبة لحالتك و لكل نشاطعملي.
مستعملاً أمثلة من واقع الحياة، يقدم لك هذا القسم فكرة توجيه لتلاميذك في نقاشهم و استخدام وسائل بسيطة – ثمرة، ورقة و أشرطة كسور (أنظر إلى المصدر ١: أشرطة كسور). ستجد أنه باستعمال هذه الوسائل، يفهِم التلاميذ مفهوم الكسور بسهولة. كذلك من خلال عمل المجموعات ومناقشة التلاميذ لنتائجهم، يكونوا قد تعرضوا لمختلف أنواع الكسور
دراسة الحالة رقم ١:استخدام عمل المجموعات لإستكشاف الكسور البسيطة
بدأ الأستاذ أوهاج درسه عن الكسور بقطع برتقالة لجزئين متساويين ثم إلى أربعة أجزاء متساوية، سائلاً التلاميذ أن يسموا الأجزاء. قدم مزيداً من الكسور البسيطة، عارضاً كلاً منها بتطبيق قطعاً مستطيلة من الورق. أكّد على أن نصفين يكونان الكل، إلخ
بعد ذلك، ناقش مع تلاميذه كيف أن الأشياء مشتركة في واقع الحياة. بما أن فصله كان كبيراً، قرر أن يقسم الفصل إلى مجموعات صغيرة متكونة من ثلاثة تلاميذ. رسم دائرة، ومستطيل و مربع على السبورة و طلب من كل تلميذ أن يختار شكلاً واحداً و يرسمه ستة مرات. طلب منهم أن يظلّلوا رسوماتهم ليوضحوا
نصف
نصفين
ربع
ربعين
ثلاثة أرباع
أربعة أرباع
كل تلميذ في المجموعة عرض للآخرين ما فعله. سألهم إن استطاعوا أن يروا أي أنماط في رسوماتهم. فأشار بعض التلاميذ إلى أن ربعين هي مثل نصف واحد، إلخ. تشاركوا هذا الإكتشاف مع الأعضاء الآخرين في نفس المجموعة و مع الفصل.
بالرغم من أن هذا الفصل كان كبيراً، وجد الأستاذ أوهاج أن هذا النهج بالعمل في مجموعات يعني أن كل التلاميذ قد إكتشفوا فهماً مبدئياً للكسور المتساوية من رسوماتهم و تفاعلاتهم مع بعضهم البعض. شعر أيضاً أنهم مستعدون بشكل جيد للدرس التالي الذي خططه.
نشاط رقم ١:إستخدام أشرطة الكسور
أعمل بعض أشرطة الكسور (أنظرإلى المورد ١: أشرطة كسور) و أعرضهم على تلاميذك، طالباً منهم أن يصنعوا بعضها في البيت للدرس القادم. حاول الأنشطة بنفسك، آخذ في الإعتبار الصعوبات التي يمكن أن يجدها تلاميذك و كيف يمكنك مساعدتهم.
إبدأ باستعمال أشرطتك، بعرضها على الفصل كأمثلة.
الآن أقسم فصلك إلى مجموعات من ستة تلاميذ، طالباً منهم أن يستعملوا أشرطة كسورهم ليعرض كل منهم بعض الكسور و يقارنها.
بينما التلاميذ يعملون، إسأل نفسك بعض الأسئلة:
هل العدد في كل مجموعة كان مناسب حيث سمح لكل التلاميذ بالمشاركة
هل استخدام أشرطة الكسور مفيداًً لفهم المفهوم؟
كيف يمكن تطوير هذا الدرس؟
هل إستمتع التلاميذ بالدرس؟
دراسة الحلقة ٢:
هذا الجزء مبني على خبرة استخدام أشرطة الكسور للعمل عملياً، لجمع و طرح كسور بسيطة. باستخدام التوضيح لكل الفصل، و العمل في أزواج، ستكتشف ما هي الطرق الأفضل التي تساعدك و تلائمك أكثر.
بينما تعمل، أسأل نفسك هذه الأسئلة:
هل يجب أن تساعد الكثيرين؟ إذا كانت الإجابة بنعم، لماذا هذا في إعتقادك؟
هل أنت و التلاميذ مستمتعون بالأنشطة العملية؟
هل تعتقد أن الفصل يتعلم بهذه الطريقة أفضل مما لو أخبرتهم فقط؟ كيف عرفت ذلك؟
دراسة حالة رقم ٢:عمل أكثر مع أشرطة الكسور
أحضر الأستاذ محجوب لدرسه شريط كسور كبير للأعشار، كان قد عمله. طلب من كل تلميذ أن يعمل مثله، مستخدماُ الموارد التي جهزها. بعد 15 دقيقة، ساعد التلاميذ في استخدام أشرطة كسورهم ليجدوا إجابات لهذه الأسئلة:
بكم يزيد 10/8 على 10/5؟
ما الفرق بين 10/8 و 10/5؟
كم 10/8 – 10/5؟
كتب على السبورة حاصل 10/8 – 10/5 = 10/3 و طلب من التلاميذ أن ينسخوا ذلك في دفاتر تدريباتهم.
بعد ذلك طلب من تلاميذه أن يعملوا في أزواج و يعملوا بعض الجمع لأعشار مستخدمين أشرطة كسورهم. قام بعمل بعض عمليات الجمع المثيرة مستخدماً سياقات مألوفة.
كان الأستاذ محجوب مندهشاً مما استطاع التلاميذ أن يعملوه، و لكنه أيضاً تنبه إلى أنه احتاج أن يعطي بعض التلاميذ تدريبات أكثر و وقتاً ليتحدثوا عن أفكارهم أثناء عملهم.
نشاط رقم ٢:جمع وطرح كسور بسيطة
قبل الدرس، جهز ثلاثة أقراص – قرص كامل، ربع قرص و نصف قرص، كل منها مع كل الأرباع معروضة في ( المصدر٢: أقراص كسور).
أرفع ربع القرص و نصف القرص إلى أعلى و أسأل تلاميذك ماذا يكون المجموع إذا جمعت هذين القرصين. أعط وقتاً كافياً للإجابة، و عندما تجد الإجابة الصحيحة، أكتب الحاصل على السبورة: ¼ + 4/2 = 4/3
بعد ذلك، أرفع الأقراص الثلاثة إلى أعلى و أسأل نفس السؤال.
مرة أخرى، إنتظر الإجابة الصحيحة ثم أكتب الحاصل على السبورة: 1 + ¼ + 4/2 = 4/31
الآن قسم تلاميذك إلى أزواج، و اطلب منهم أن يرسموا أقراصاً مشابهة مع أثلاث. أطلب منهم أن يعملوا عمليات جمع ليعطوها لرفقائهم و ليكتبوا العملية الكاملة و الإجابات في كل حالة.
بينما هم يعملون، طف حول الفصل و ساعد حين الحاجة. إذا كان ضرورياً أتركهم يحاولون كسوراً أخرى لترى إذا هم حقيقة يفهمون الفكرة.
أعرض بعض الكسور المختلفة على الجدار
دراسة الحلقة ٣:
يبنى هذا الجزء على مفهوم طرق الكسور و يوسع ذخيرتك الفنية من الأنشطة العملية باستخدام نموذج ( الجزء-الكل ) لإستكشاف طرق لإعطاء توضيحات واضحة عن الكسور المتكافئة. بقيامك بالنشاط العملي بنفسك قبل الدرس، ستكون قادراً على أن تتوقع أي نوع من الصعوبات قد تطرأ و كيف ستجيب عليها. ستستعمل مواد من الواقع لأن كما تعلم، ذلك سيساعد التلاميذ على ربط ما يتعلموه بالتطبيق العملي و يقدرون فائدة الرياضيات واستعمالها.دراسة حالة رقم ٣:استخدام نموذج الجزء-الكل
قررت الأستاذة أرويمة أن تستعمل نموذج الجزء-الكل لتقدم كسوراً متساوية لفصلها و لتنّمي مهاراتها في استخدام عمل المجموعات و العمل العملي.
عرفت أن استعمال مواد من الحياة اليومية ستساعد التلاميذ على الفهم أحسن. فأخذت لفصلها بعض البسكويت لتساعدها على توضيح الكسور المتساوية. أولاً، قسمت الفصل إلى مجموعات كل مجموعة من ثمانية تلاميذ و طلبت منهم أن يوضحوا كيف أن 20 قطعة بسكويت يمكن أن تشارك بالتساوي بين عدد من التلاميذ.
بعد ذلك، جعلت في كل مجموعة عدداً مختلفاً من التلاميذ. أعطت مجموعة قطعتين من البسكويت و طلبت منهم أن يتشاركوا هذه البسكويتات بين أربعة تلاميذ. رأوا أن 2 مقسومة على 4 فأعطت كل تلميذ ½ بسكويتة. كتبت على السبورة 2 مقسومة على 4 = 4/2 = 2/1.
كررت هذه المسألة مع مجموعات أخرى فأعطت 3 قطع بسكويت لتقسيمها على 6 تلاميذ.
ثم أعطت 4 قطع بسكويت إلى 8 تلاميذ، فأخذ كل منهم نصف بسكويتة.
كل مرة كتبت الكسور على السبورة 4/2، 6/3، 8/4 مع كل منها يساوي 2/1.
أخبرت التلاميذ أن هذه تسمى الكسور المتكافئة.
كانت الأستاذة أرويمة مسرورة من استجابة الفصل لدرسها في الرياضيات مستخدمة البسكويت لتوضح الكسور المتكافئة.سألت التلاميذ في مجموعات من أربعة تلاميذ، أن يحاولوا حل هذه المسائل معاً
النشاط الأساسي: كسور متساوية باستخدام حل المسائل
طلب من تلاميذك أن يعملوا في أزواج لحل هذه المسألة: أنت أُعطيت 5/2 من كيكة. أرسم الكيكة و وضح قطعتك.
الآن أطلب منهم أن يرسموا عشرة علامات ضرب في رسمهم لقطعة ال5/2 من الكيكة و يوجدون إلى كم سيحتاجون ليملأوا كل الكيكة.
بعد دقائق من مناقشتهم مع رفقائهم، أطلب من بعض التلاميذ أن يوضحوا كيف توصلوا إلى حلولهم. ناقش الإجابات و الطرق التي استخدموها. أوضح أن الكسر 10\25 مثل 5/2 و هذه تسمى الكسور المتكافئة.
أعرض لهم أن هناك أكثر من طريقة لعمل المجاميع، حتى يشعر التلاميذ بالإرتياح أياً كانت الطريقة التي استخدموها.
للتقويم الذاتي، استخدم بعد الدرس، أسئلة مثل تلك الواردة في المصدر٣ و اسأل نفسك أسئلة عن استخدامك لنشاطات العملية و الموارد.
المصدر ١: أشرطة الكسور
بعض أشرطة الكسور موضحة أدناه. يمكنك تصميمها بأي ورقة بواسطة الطي و/أو القياس.

المصدر ٢: أقراص الكسور
هذه تعمل برسم دائرة و تقسيمها إلى أنصاف، أرباع، إلخ، بواسطة الطي.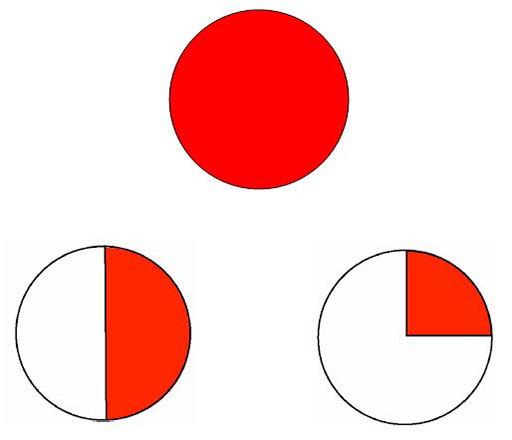
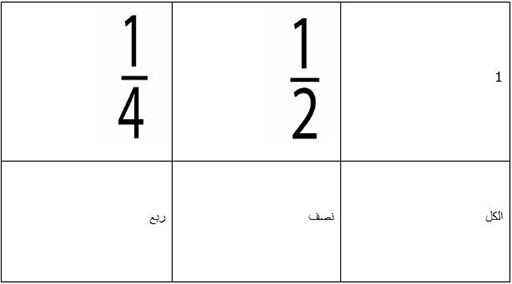
المصدر ٣: أسئلة للتقويم الذاتي
حين تجيب على هذه الأسئلة، من المهم جداً أن تكون في غاية الأمانة و تتعرف على نقط ضعفك، حتى تحسن مهاراتك المهنية و تصبح معلماً أفضل.
هل أنا أشعر بالثقة أكثر في استخدام عمل المجموعات و هل ساعد ذلك فهم التلاميذ؟
هل استخدام مجموعات بأعداد و أنواع مختلفة قد حسّن من دروسي و جعلها أسهل فهماً على تلاميذي؟
هل أشعر بأن العمل العملي يساعد على الفهم، و هل أنا واثق من استخدامه؟
هل أنا شغلت تلاميذي في أنشطة الرياضيات بدرجة كافية؟
هل أعطيت تلاميذي وقتاً كافياً ليؤدوا مهامهم العملية؟
كيف يمكنني تحسين تدريسي لهذا الموضوع؟
ما الذي سأغيّره في المرّة القادمة؟
أسئلة عن استعمال الأنشطةالعملية و الموارد البسيطة
هل ساعدتني هذه الأنشطة على تحقيق أهدافي التعلّمية؟
هل كانت الأنشطة مناسبة لتلاميذي؟
هل أثارت فضول و اهتمام التلاميذ؟
كيف كانت مناسبتها بشكل جيد لقدرات فصلي؟
هل الموارد المستعملة ساعدتني على تحقيق أهدافي التعلّمية؟
هل كانت الموارد مناسبة لفصلي؟
هل اثارت هذه الموارد فضول واهتمام التلاميذ؟
كيف كانت مناسبتها بشكل جيد لقدرات فصلي؟
إلى أى مدى كانت الدروس ممتعة؟