Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Thursday, 25 April 2024, 5:16 PM
Immunization Module: Vaccine Supply and Stock Management
Study Session 5 Vaccine Supply and Stock Management
Introduction
This study session deals with how to determine vaccine needs and how to keep your stock of vaccines in a reliable way, so that your immunization programme will not be interrupted as a result of shortage of supply. We also explain how to avoid wastage of vaccines by reducing the risk that the stock will pass its expiry date. The study session involves a lot of calculations using basic mathematics (addition, subtraction, multiplication and division) and using letters to represent values that you will need to measure or estimate. You are advised to apply your own data after each of the examples given here, to help you understand how the calculations apply in your setting.
Learning Outcomes for Study Session 5
When you have studied this session, you should be able to:
- 5.1 Define and use correctly all of the key words printed in bold. (SAQs 5.1, 5.3 and 5.4)
- 5.2 Calculate the size of the target population in your community and forecast their vaccine needs, using three different methods. (SAQs 5.1 and 5.2)
- 5.3 Calculate vaccine wastage rates and wastage factors and apply them to orders of vaccine stocks to minimise wastage. (SAQs 5.1 and 5.3)
- 5.4 Calculate the minimum and maximum quantities of vaccines required for a stated supply period and manage the critical stock level effectively. (SAQ 5.4)
5.1 Estimating vaccine needs
Vaccine management involves estimating the number of vaccine doses, diluents and injection equipment (e.g. syringes, needles) needed for a particular population over a stated supply period. In order to run an efficient and effective immunization session you need to have an adequate supply of vaccines of acceptable quality. This is essentially dependent on reliable planning and monitoring. You might have heard from mothers in the community that the health facility ran out of vaccines and their child could not be immunized. On the other hand, health facilities may have an excess stock of vaccine that has passed its expiry date and has to be thrown away. You should try to ensure that these situations do not arise in your Health Post (Figure 5.1).

Before we move on, remind yourself of the meaning of some key terms from previous study sessions.
What is the expiry date?
The expiry date is the (international calendar) date after which a vaccine, diluent or other consumable item should not be used for the purpose of immunization, because of possible loss of potency (vaccines; diluents) or durability (syringes, needles and other items).
Potency refers to the ‘strength’ or ‘effectiveness’ of a vaccine; durability refers to the time period that equipment such as syringes or needles remain in good condition (how long they last).
What is a diluent?
A diluent is a liquid used to reconstitute a freeze-dried vaccine. Each vaccine has its own diluent which should not be used to reconstitute any other vaccine.
Determining your vaccine needs accurately is important because it allows you to manage your immunization programme efficiently. Good vaccine management:
- enables you to use vaccines efficiently, and reduce wastage
- avoids shortages or excess accumulation of vaccines.
If the vaccine needs for your Health Post are not estimated correctly, and the wrong amounts are supplied by the health centre, this may result in shortage of vaccines or excess stock.
What is the problem if you order excess stock?
There is the risk that the vaccines will pass their expiry date before you need to use them, so they will be wasted.
We now consider how you can determine the vaccine needs for your Health Post. There are three methods based on:
- size of the target population for immunization
- previous vaccine consumption data
- size of the scheduled immunization sessions.
You will learn about each of these methods in the sections that follow. But you should note that vaccine requirements are likely to vary a lot from one kebele to another; the stocks required for your immunization programme may be very different from the examples used in this study session.
5.2 Estimating vaccine needs based on the size of the target population
5.2.1 What is the target population?
The target population is the number of people who are eligible for vaccination with a particular vaccine. We use the letters ‘pt’ to represent the target population in calculations.
- [You learnt about tetanus toxoid (TT) vaccine and all the other the vaccines available in the EPI in Ethiopia in Study Sessions 2 and 3]
- For BCG vaccine, the target population is all live births (i.e. complete expulsion from the mother, regardless of duration of pregnancy, showing any evidence of life).
- For all other vaccines in the Expanded Programme on Immunization (EPI) in Ethiopia, the target population is all surviving infants (i.e. survive to their first birthday).
To calculate vaccine needs based on the target population, you need to know the size of the target population, the number of doses required according to the EPI schedule, and the percentage immunization coverage rate you have been given as the target in your annual activity plan (Figure 5.2).
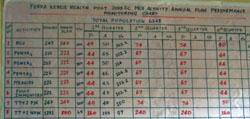
In Figure 5.2, the column headed ‘eligible’ gives the number in the target population for each vaccine. You can see that the health workers in this Health Post planned to immunize 100% of the eligible children and 100% of the pregnant women (TT+2 PW, pregnant women receiving more than 2 doses of TT vaccine). Columns headed P refer to ‘planned’ numbers for immunization, and A are the ‘actual’ numbers immunized — in the first quarter of the year, they exceeded their targets for all categories except TT+2 NPW (non-pregnant women of childbearing age receiving more than 2 doses of TT).
Next, we will show you how to use data from an area similar to that of your kebele to calculate the target population for vaccination, so you can construct an annual activity plan for immunization like the one shown in Figure 5.2.
5.2.2 Calculating numbers in the target population
Table 5.1 (on the next page) shows an estimate of the target population for immunization in a kebele with a total population of 5,000. A figure of 4% of the Ethiopian population is usually taken to estimate the coverage required for all live births and surviving infants. You can assume that (on average) about 23% of the Ethiopian population will be women of childbearing age, of whom about 4% will be pregnant in a typical year.
| Category | % of total population | Estimated number in target population |
|---|---|---|
| Live births | 3.6 | 180 |
| Surviving infants | 3.4 | 170 |
| Women of childbearing age (pregnant and non-pregnant) | 23 | 1,150 |
You estimate the target population by multiplying the total population by the percentage in a particular category; for example in Table 5.1:
Expressing a percentage as a decimal number is easy, e.g. 90% is the same as 0.9; 23% is the same as 0.23, and 4% is the same as 0.04.
- The estimated number of women eligible for TT vaccination (Figure 5.3) is 5,000 x 23% (or 0.23) = 1,150
- The estimated number of children eligible for all other EPI vaccines is 5,000 x 4% (or 0.04) = 200, if you take the simple average of 4%. If you use the Ministry of Health indicators of live births (3.6%) and surviving infants (3.4%), the numbers will be 170 and 180 respectively.

Look back at Figure 5.2. What was the estimated target population eligible for TT immunization in Fura kebele in the year shown?
The estimated eligible population for TT vaccination was 1,478 women of childbearing age (247 pregnant and 1,231 non-pregnant) in Fura that year; this is 23% of the total population of 6,348 in the kebele.
5.2.3 Calculating required doses based on the immunization schedule
In addition to calculating the number of people in the target population, you also need to know the number of doses required in the EPI schedule in order to immunize everyone (total coverage). You learned about the EPI schedule in Study Sessions 2 and 3, but we repeat the key points in Table 5.2. We use the letters ‘dn’ to represent the number of doses in calculations.
| Vaccines | Schedule by age | Number of doses in schedule (dn) |
|---|---|---|
| BCG | At birth | 1 |
| Pentavalent | At 6, 10 and 14 weeks | 3 |
| Polio (OPV) | At birth, 6, 10 and 14 weeks | 4 |
| PCV10 | At 6, 10 and 14 weeks | 3 |
| Measles | At 9 months | 1 |
| Tetanus toxoid | On reaching childbearing age Ideally all women of childbearing age should receive five doses of tetanus toxoid. | At least 2 |
If you have an estimated 200 surviving infants in your kebele, how many doses of pentavalent vaccine would be needed to complete the EPI schedule for all these children? Use the data on % of total population in Table 5.1.
The target population is 170 surviving infants, so you would need 510 doses to complete the EPI schedule for all of them, because each surviving infant should have three doses of pentavalent vaccine.
5.2.4 Immunization coverage targets
You now know how to calculate the annual vaccine needs for immunization of everyone in the target population. The EPI policy is to immunize 100% of the target population, but you may not be able to reach everyone in the target population in one year (for example, if your kebele includes very remote areas). Your annual action plan will include a percentage target from the woreda health office for the immunization coverage rate — the percentage of the eligible population that has been agreed as your objective for immunization with each of the EPI vaccines this year. The performance of your Health Post will be measured against this target.
If the annual target is less than 100% for a particular vaccine, you can estimate the number of vaccine doses you will actually need as follows. Start with the number of doses required to immunize everyone in the target population (i.e. total coverage), and multiply that number by the agreed (lower) percentage target for immunization coverage in your setting. We use the letters ‘ic’ to represent the percentage target for immunization coverage in calculations. Now look at the example in Table 5.3. (Your targets will be different.)
| Vaccine | Number of doses for 100% coverage | % coverage target (ic) | Actual number of doses needed |
|---|---|---|---|
| BCG (1 dose) | 200 | 90 | 180 |
| Polio (4 doses) | 800 | 90 | 720 |
| Pentavalent (3 doses) | 600 | 100 | 600 |
| PCV10 (3 doses) | 600 | 90 | 540 |
| Measles (1 dose) | 200 | 80 | 160 |
| Tetanus toxoid (2 doses) | 2,300 | 65 | 1,495 |
How many doses of TT vaccine would you need to immunize the eligible women in Table 5.3 with three doses per woman, if you increased the percentage coverage target to 70%?
Total 100% coverage with three doses would require 3,450 doses. If the coverage target is 70%, the actual doses required would be 3,450 x 0.7 = 2,415 doses.
Note that you can use the same method of calculation to estimate the number of ampoules of specific diluents required to reconstitute the freeze-dried vaccines (BCG and measles), and your requirement for injection equipment.
5.2.5 Vaccine wastage rates and wastage factors
Using calculations like the one in Table 5.3 enables you to determine the number of vaccine doses you need. However, some vaccine doses may be wasted during the year for various reasons (Box 5.1 on the next page). The wastage rate is the percentage of vaccine doses that are wasted. The general guideline on the amount of vaccine wastage that is considered acceptable for different types of vaccines is also shown in Box 5.1.
Box 5.1 Vaccine wastage
Some reasons for vaccine wastage:
- Some unused doses may have to be thrown away, e.g. because they have passed their expiry date or lost their labels.
- Some doses may be spoilt for one reason or another (e.g. vaccines damaged by storage at the wrong temperature).
- Some vials or ampoules may be broken during transport and handling.
Acceptable vaccine wastage rates:
- For liquid vaccines supplied in single or two-dose vials (e.g. pentavalent vaccine and PCV10), a wastage rate of 5% is acceptable.
- For OPV, a wastage rate of 10% is considered acceptable.
- For liquid vaccines supplied in multi-dose vials of 10 or more doses, a wastage rate of 15% is acceptable.
- For reconstituted vaccines, wastage rates of 50% for BCG and 25% for measles vaccine are considered acceptable.
Calculating the wastage factor
The wastage factor is the factor (number) that you multiply your estimated vaccine needs by, in order to allow for some doses being wasted. We use the letters ‘wf’ to represent the wastage factor in the following equation:
- wastage factor (wf) = 100 ÷ (100 minus the % wastage rate)
- where the wastage rate is the number of doses wasted, expressed as a percentage.
Note the ‘brackets first’ rule. In equations that include brackets around some of the numbers, you always calculate the answer to whatever is inside the brackets first, before you do anything else.
If the wastage rate is 30%, what is the wastage factor?
Wastage factor = 100 ÷ (100 – 30) = 100 ÷ 70 = 1.43 Therefore, if 30% of the doses are wasted, the wastage factor will be 1.43.
Now you have learned how to calculate the basic values you need to estimate your vaccine needs for the target population. These values are the target population (pt), the number of doses in the schedule (dn), the immunization coverage target (ic) and the wastage factor (wf).
5.2.6 Calculating annual vaccine needs from the size of the target population
To calculate the annual vaccine needs for your immunization programme from the size of the target population, you need to multiply together the four values explained in Sections 5.2.1 to 5.2.4 of this study session. The calculation can be summarised using the equation shown below:
- Annual vaccine needs = pt x dn x ic x wf
The equation uses the following values:
- target population (pt)
- number of doses in the schedule (dn)
- target immunization coverage (ic) expressed as a decimal number (not a percentage)
- wastage factor (wf).
Calculate the annual vaccine needs for pentavalent vaccine for a target population of 200 surviving infants, using the equation given above. Remember that three doses of this vaccine per child are needed for full immunization. Assume the target coverage rate is 90% and the wastage factor is 1.33 in this example.
The calculation is as follows:
- number of surviving infants (pt) = 200
- number of pentavalent doses in the EPI schedule (dn) = 3
- target coverage rate (ic) expressed as a decimal number = 0.9 (90%)
- wastage factor (wf) = 1.33
Annual pentavalent vaccine needs = pt x dn x ic x wf = 200 x 3 x 0.9 x 1.33 = 178 In this example, 718 doses of pentavalent vaccine would be needed annually. Remember that the requirement in your own kebele may be different.
Now we turn to the second method of calculating vaccine needs.
5.3 Estimating vaccine needs on the basis of previous consumption
This method is based on the consumption of vaccines during the previous reporting period (usually the previous year). Some adjustment may be necessary if you believe that there has been any increase in the population size since the previous vaccine consumption was recorded. This method is useful for a Health Post where the stock management is good, but there is insufficient information on immunization objectives and targets for the next action plan. It is also useful when placing short-term orders.
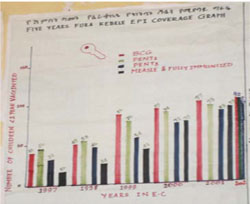
In a kebele where stock management is efficient, there is likely to be good information on previous vaccine consumption. For example, you can probably see from the red bars in Figure 5.4 that 97 babies were immunized at birth with BCG in this kebele in 2001 (Ethiopian calendar). So this number could be used to predict the BCG vaccine requirement in the following year.
5.3.1 Calculating annual vaccine needs from previous consumption
For this calculation, we use an equation based on the stock of vaccine at the beginning and end of a particular period, the vaccines received during that period, and the vaccines lost, destroyed or thrown away during that period. The equation is given below:
- Annual vaccine needs (in doses) = (i+r) – (f+l)
Remember the ‘brackets first’ rule; calculate the sums inside the brackets first, before you do anything else.
The equation includes the following numbers of doses:
- initial vaccine stock at the beginning of the period (i)
- vaccines received during the period (r)
- stock remaining at the end of the period (f)
- lost, destroyed or expired doses (l).
Use the above equation to calculate the annual vaccine needs (in doses) for pentavalent vaccine in a particular kebele, in which the initial stock at the beginning of the year was 250 doses, and the quantity received during the year was 1,250 doses. At the end of the year there were 500 doses remaining in stock. The quantity lost during the year was 125 doses.
The answer is calculated as follows:
Annual vaccine needs = (i+r) – (f+1) = (250 + 1,250) – (500 + 125) doses = 1,500 – 625 doses = 875 doses In this example, the estimated annual pentavalent vaccine need based on previous consumption is 875 doses.
In the example given in Section 5.2.5, the estimated annual pentavalent vaccine need, based on the size of the target population, was 718 doses. However, the estimate based on the previous year’s consumption (see above) was 875 doses. If both these imaginary examples had come from the same Health Post, what explanations could you suggest for the difference between the two estimates?
Clearly the Health Post staff used more vaccine doses (875) in the previous year than was predicted from the size of the target population (718). There are several possible reasons for this, including:
- There were more surviving infants in the kebele than the 200 estimated from calculating 4% of the total population size of 5,000.
- The Health Post staff achieved a higher immunization coverage rate in the previous year than the 80% target they were asked to deliver.
- They wasted more doses of vaccine than expected.
5.4 Estimating vaccine needs based on the size of immunization sessions
Now we show you how to calculate vaccine needs based on the size of immunization sessions. This method is appropriate if you cannot determine the rates of vaccine wastage, or vaccine stock management is not good. The equation you should use to estimate the annual vaccine needs by this method is given below:
Annual vaccine needs = posts x weeks x sessions x vials x doses, where:
- posts = number of immunization sites
- weeks = number of weeks the service is delivered during the year
- sessions = number of immunization sessions per week
- vials = number of vials opened per immunization session
- doses = number of doses per vial.
Table 5.4 shows how to calculate vaccine needs based on the size of immunization sessions in an imaginary example, using a vaccine supplied in multi-dose vials containing 10 doses per vial.
| immunization posts | weeks delivered | sessions per week | vials per session | doses per vial | total doses | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | x | 48 | x | 2 | x | 1 | x | 10 | = | 960 |
So the vaccine needs for this particular multi-dose vaccine, based on the size and number of vaccination sessions = 960 doses per year.
Why do you think an estimate based on the size of the immunization sessions is likely to be higher than one based on previous consumption?
An estimate based on the size of the immunization sessions assumes that all of the scheduled immunization sessions will actually be held for each of the scheduled weeks in the year. But if some sessions cannot be held (for example, if there was a shortage of vaccine, or if the health worker was ill), then the actual number of vaccine doses given would be lower than estimated using the method illustrated in Table 5.4.
5.5 Ordering vaccines
In the previous section you learnt how to estimate vaccine needs. Vaccines are very expensive, so it is important to ensure that the ordered vaccines will be used and not spoiled. The World Health Organization (WHO) recommends that every order for vaccines should take into account the considerations in Box 5.2. There are some new terms in this box which are explained below it.
Box 5.2 Considerations for vaccine ordering
Health facility staff should always use an EPI Vaccine and Injection Materials Stock Record (see Figure 5.5) to help them to:
- Avoid stock shortages, especially when mass immunization campaigns are planned.
- Avoid stock excesses, by not ordering excess stock, or exceeding the recommended storage periods.
- Avoid situations where vaccines expire during their storage period.
- Ensure that the other necessary stocks (e.g. diluents, syringes, needles; wick and paraffin or kerosene for refrigerators, etc.) are ordered at the same time as the vaccines.
- Organise stock using the principle of ‘bundling’ for all supplies required delivering an immunization session.
- Ensure that there are adequate cold chain storage facilities (both in capacity and temperature; see Study Session 6).

Bundling refers to the practise of organising related stock all together in ‘bundles’ consisting of the correct numbers of all the items you need during an immunization session:
- good quality vaccines and diluents
- auto-disable (AD) syringes (or single-use disposable syringes and needles, if these are still used)
- safety boxes, etc.
Auto-disable (AD) syringes were mentioned in Study Session 4, and are specially modified disposable syringes with a fixed needle; an AD syringe is automatically disabled after it has been used once, because the plunger cannot be pulled back a second time. The WHO recommends that immunization programmes use AD syringes for all vaccinations, to prevent re-use of contaminated injection equipment.
The cold chain is fully described in Study Session 6, and refers to the network of refrigerators, cold stores, freezers, cold boxes and vaccine carriers, and their efficient organisation and maintenance, so that vaccines are kept at the right temperature at all times. This ensures that vaccines keep their potency during their transportation and storage at all stages, from leaving the factory to the point of administration to the target population.
Storage of vaccines is a major challenge. Vaccines are easily damaged during storage if the cold chain is not maintained. Therefore it is important to divide the vaccine supply into manageable periods for the purpose of ordering stocks. A Health Post will usually have a shorter supply period (four weeks) than a health centre. The next section explains how to calculate the quantities of vaccine needed for a specific supply period.
5.5.1 Calculating quantities of vaccine for a particular supply period
The vaccine needs for a specific storage or supply period (in this case, 12 months or 48 working weeks) can be calculated using the following equation:
qperiod = (qyear ÷ 12) x psupply when the supply period is given in months, or qperiod = (qyear ÷ 48) x psupply when the supply period is given in working weeks. where:
- qperiod = vaccine needs for the period
- qyear = annual vaccine needs
- psupply = supply period (in months or weeks).
You can see an example of vaccine needs calculated in weeks in the following question.
If the number of doses of vaccine required for one year in an imaginary kebele is 2,000, how many doses would be needed for a two-week period?
In this example, the annual vaccine needs qyear = 2,000 and the supply period psupply is 2 weeks.
The vaccine needs for one week would be 2,000 doses ÷ 48 working weeks.
So the vaccine needs for the period (qperiod) of 2 weeks is (2,000 ÷ 48) x 2 = 83 doses.
Therefore, 83 doses would be required for a two-week period in this example.
5.5.2 Calculating the minimum stock level
The time between the date of ordering vaccines and the date when you collect them may not be as soon as you would wish it to be. There may be an increase in vaccine demand that you want to respond to quickly, but you may find there are unexpected delays in restocking. Therefore, you should always aim to keep a minimum amount of vaccine in stock. The minimum stock level is the minimum number of vaccine doses that should be in the refrigerator when the next supply of vaccines is collected. Usually, the minimum stock is taken as 25% of the total vaccine needs for the supply period.
The minimum stock level can be calculated using the following equation:
- smini = qperiod x 25% (or 0.25)
where smini is the minimum stock level and qperiod is the vaccine needs for the period.
Imagine that at a particular Health Post, the number of doses of oral polio vaccine (OPV) required for a 2 week supply period is 80. If the minimum stock should be 25% of the total vaccine needs for the supply period, what should the minimum stock level be at this Health Post when the next supply of vaccine is collected from the health centre? (Remember that 25% is expressed as 0.25 in calculations.)
The number of doses of OPV required for 2 weeks is 80.
The percentage required as minimum stock is 25% (0.25).
So the minimum stock is 80 x 0.25 doses, or 20 doses.
This means that there should be at least 20 doses of OPV in stock at this Health Post when the next supply of vaccine is collected.
5.5.3 Calculating the maximum stock level
You have learned that vaccines are easily damaged and that they are very expensive. It is not good practice to keep an unnecessary amount of vaccine in stock. The maximum stock level is the maximum number of vaccine doses that should be present in the refrigerator immediately after a new supply has been collected from the health centre.
The maximum stock level can be calculated using the following equation:
- smaxi = qperiod + smini
where smaxi is the maximum stock level, qperiod is the vaccine needs for the period, and smini is the minimum stock level.
Think again about the Health Post where the number of doses of OPV needed for a 2-week supply period is 80 and the minimum stock level is 20 doses. What should the maximum stock level of OPV be in this Health Post?
The number of OPV doses needed at this Health Post for a 2-week period is 80, and the minimum stock level is 20 doses, so the maximum stock level is (80 + 20) = 100 doses. So there should be no more than 100 doses of OPV in stock when the next supply of this vaccine is collected.
If your supplies of vaccine exceed your maximum stock level, it may be wise to consider returning some vials to the higher level.
5.5.4 Calculating the critical stock level (or ‘time to order’)
It is important to be aware of your vaccine stock, and to place your next order at the right time. The critical stock level (or ‘time to order’ level) is the number of vaccine doses in stock at the time when it is absolutely necessary to place a new order. ‘Time to order’ calculations take into account the level of vaccine consumption while waiting for the new supply. This precaution is necessary to prevent the vaccine stock from dropping below the minimum stock level before the new order can be collected. The delivery time is the time interval between the day the vaccines are ordered and the day that you collect them from the health centre.
The critical stock level can be calculated using the following equation:
- scritical = qdelivery + smini , where:
- scritical is the critical stock level
- qdelivery is the number of doses needed during the delivery time, and
- smini is the minimum stock level.
- qdelivery = (qperiod x tdelivery) ÷ n , where:
The number of doses required during the delivery time (qdelivery) can be calculated using the following equation:
- tdelivery is the number of days between placing the order and collecting new vaccines
- n is the number of days in the supply period (i.e. the period that the health facility maintains its vaccine stocks at, or above, the minimum level).
Now attempt Activity 5.1 to calculate the critical stock level for an imaginary Health Post. You will need paper and a pen or pencil to help you make the calculations.
Activity 5.1 Calculating the critical stock level
At a particular Health Post, it often takes 2 working days for the HEW to collect her new supply of vaccines after ordering them from the health centre, which is 15 km away along difficult tracks. The number of doses of OPV she needs for a supply period of 2 weeks is 80 doses.
What is the critical stock level (or ‘time to order’ level) for OPV at this Health Post? Assume that the minimum stock level is 25% of the number of doses needed for the 2-week supply period (10 working days).
Write down all your calculations so that it is clear how you reached your answers. Do this before you check our answer below.
Answer
The calculation of the critical stock (or ‘time to order’) level can be done using the equations given above Activity 5.1. First, calculate the number of doses you will need during the delivery time (qdelivery) by using the equation:
- qdelivery = (qperiod x tdelivery) ÷ n
In this Health Post, qperiod is 80 doses of OPV, tdelivery is 2 days, and the supply period is 10 working days (2 weeks) so n is 10.
- qdelivery = (80 x 2) ÷ 10 = 16 doses
The minimum stock level (smini) is 25% of 80 doses, which is 20 doses. The critical stock level (scritical) is calculated using the equation:
- scritical = qdelivery + smini
In this Health Post, qdelivery is 16 doses and smini is 20 doses, so:
- scritical = (16 + 20) = 36 doses.
So the staff at this Health Post should place an order for OPV when the critical stock level is reached at 36 doses.
In the next study session you will learn about keeping vaccines and diluents safe and effective by maintaining the cold chain. This is vitally important in reducing wastage, as well as maintaining the potency of the vaccines.
Summary of Study Session 5
In Study Session 5, you have learned that:
- Vaccine management is important because vaccines are easily damaged and they are very expensive.
- Accurate estimation of all stock requirements avoids shortages and prevents wastage from excessive orders; good vaccine stock management is essential to the smooth running of immunization sessions.
- There are three methods of estimating annual vaccine needs, based on:
- size of the target population
- previous consumption levels
- size of immunization sessions.
- These methods can also be applied to estimates of other immunization supplies, such as diluents and injection equipment.
- It is essential to keep the EPI Vaccine and Injection Materials Stock Record up to date; this will help you to avoid stock shortages and stock wastage.
- It is good practise to organise stocks of vaccines, diluents, syringes, needles and safety boxes together in bundles.
- It is important to ensure that vaccine stocks do not fall below the recommended minimum level, or rise above the recommended maximum level, and that you order new supplies when the stock falls to the critical level.
Self-Assessment Questions (SAQs) for Study Session 5
SAQ 5.1 (tests Learning Outcomes 5.1, 5.2 and 5.3)
Imagine that you are working in a kebele with a total population of 5,700, and that 5% of the total population are children aged 0 to 11 months. There is only one immunization site — your Health Post. You have been given a target of 90% immunization coverage for pentavalent vaccine for the year. The wastage rate has been agreed as 5%.
- Based on the national EPI schedule for this vaccine, calculate the annual pentavalent vaccine needs, based on the size of the target population in this kebele.
Answer
The equation for calculating the annual vaccine needs, based on the size of the target population, is:
- Annual vaccine needs = pt x dn x ic x wf where:
- pt is the target population – for pentavalent vaccine this is the number of children aged 0–11 months (calculated below)
- dn is the number of doses of vaccine in the recommended schedule — this is 3 for pentavalent vaccine
- ic is the target immunization coverage rate — in this example it is 90%
- wf is the wastage factor (calculated below)
The number of children aged between 0–11 months is 5% (0.05) of the total population of 5,700, which is:
- 5,700 x 0.05 = 285 children in this age group (5% expressed as a decimal number is 0.05)
The wastage factor is calculated from the wastage rate of 5% using the equation:
- Wastage factor (wf) = 100 ÷ (100 – % wastage rate)
So for a wastage rate of 5%:
- wf = 100 ÷ (100 – 5) = 100 ÷ 95 = 1.05
Using the equation below to calculate the annual vaccine needs based on the target population size:
- pt x dn x ic x wf = 285 x 3 x 0.9 x 1.05 = 808 doses
So the annual pentavalent vaccine needs, based on the size of the target population in this kebele, is 808 doses.
SAQ 5.2 (tests Learning Outcomes 5.2)
Imagine that in your kebele you plan to deliver two sessions of immunization per week for 45 weeks of the year. Your Health Post is provided with PCV10 (Synflorix) vaccine in multi-dose vials of 2 doses per vial, and at each immunization session 5 vials are used.
- Estimate the annual PCV10 vaccine needs for the Health Post, based on the size of the immunization sessions.
Answer
The equation for calculating annual vaccine needs based on the size of the immunization sessions is as follows:
- Annual vaccine needs = posts x weeks x sessions x vials x doses; where (for PCV10 vaccine in this example):
- posts is the number of immunization sites, which is 1
- weeks is how many weeks the immunization site operates, which is 45
- sessions is the number of sessions per week, which is 2
- vials is the number of vials used per session, which is 5
- doses is the number of doses per vial, which is 2.
So the annual vaccine needs for DPT in this example is:
- 1 x 45 x 2 x 5 x 2 = 900 doses.
SAQ 5.3 (tests Learning Outcomes 5.1 and 5.3)
If the wastage rate for oral polio vaccine (OPV) is 10%, what wastage factor would you need to use when calculating the annual OPV needs, based on the size of the target population?
Answer
The wastage factor is calculated from the wastage rate (expressed as a percentage), using the following equation:
- Wastage factor (wf) = 100 ÷ (100 – % wastage rate)
In this example, the wastage rate for OPV has been set at 10%. So the wastage factor is:
- wf = 100 ÷ (100 – 10) = 100 ÷ 90 = 1.11
Therefore, the wastage factor is 1.11.
SAQ 5.4 (tests Learning Outcomes 5.1 and 5.4)
- a.How much PCV10 vaccine would be required by the Health Post mentioned in SAQ 5.2 for a 2-week period?
- b.What is the minimum stock level for PCV10 vaccine for a 2-week period for this Health Post?
- c.What is the maximum stock level for PCV10 vaccine in the same period?
Answer
- a.In the example given in SAQ 5.2, there are two immunization sessions per week. Five multi-dose vials of PCV10 each containing 2 doses is used per session, so 20 doses are needed per week. Therefore the number of doses required for a 2-week supply period in this kebele is 40 doses.
- b.The minimum stock level is generally taken to be 25% (or 0.25) of the requirement for the supply period, which in this example is 2 weeks. The equation needed to calculate the minimum stock level for a 2-week period is:
- smini = qperiod x 0.25 (25% expressed as a decimal number is 0.25)
- where qperiod is the number of doses required for the supply period, which in this example is 40 doses.
- smini = 40 x 0.25 = 10 doses.
- So the minimum stock level for PCV10 vaccine for a 2-week period in this kebele is 10 doses.
- c. The maximum stock level for PCV10 for a 2-week period in this kebele is calculated from the following equation:
- smaxi = qperiod + smini smaxi = 40 + 10 = 50 doses
- d.So the maximum stock level for PCV10 vaccine for a 2-week period in this kebele is 50 doses.