Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Wednesday, 4 February 2026, 12:42 PM
TI-AIE: Using number games: developing number sense
What this unit is about
‘Number sense’ is a term that is often used but is quite hard to define. In general, it refers to a student’s ability to work with numbers flexibly and fluidly. Number sense involves giving meaning to numbers – that is, knowing about how they relate to each other and their relative magnitudes. It is also about the effect of mathematical operations on numbers, such as whether multiplication of a given number by another would make the number bigger or smaller. Having a sense of number is vital for the understanding of numerical aspects of the world.
Learning and improving your sense of number is a lifelong activity that starts with children. In school it requires exploring and playing with numbers, and being encouraged to think about patterns and relationships between numbers. In school mathematics this element of playing and having fun with numbers often gets missed out. This unit aims to address this by giving ideas for identifying and using number games as activities that offer rich learning opportunities to help your students develop their sense of numbers.
What you can learn in this unit
- Some ideas to develop and strengthen your students’ sense of number.
- How to use number games as a teaching strategy to stimulate engagement, participation and mathematical reasoning.
This unit links to teaching requirements of the NCF (2005) and NCFTE (2009) and will help you to meet those requirements, outlined in Resource 1.
1 Using games for developing number sense
Pause for thought Think back to when you were a child. Did you learn anything about numbers outside of school? For example, you might have learned to count prior to attending school, or you might have come to know about money, age or sharing things equally from your life outside of school. How did such learning happen? |
Playing games is something children do from an early age. It is generally accepted that playing games stimulates the development of social interaction, logical and strategic thinking, sometimes competitiveness, or at other times teamwork and togetherness.
Games can give a sense of suspense, joy, frustration and fun. Research literature has shown that using games in teaching mathematics leads to an improved attitude towards mathematics, enhanced motivation and support for the development of children’s problem solving abilities (Ernest, 1986; Sullivan et al., 2009; Bragg, 2012). It is argued that the mathematical discussions that happen while playing mathematical games leads to the development of mathematical understanding (Skemp, 1993).
This unit gives examples of some tried and tested number games to help develop the number sense of students. It will also discuss how to spot good number games and learn to identify the learning opportunities the games can offer for students.
The first activity is an example of a game that helps to develop the understanding of number relationships. It uses a mathematical tool the students are already familiar with: the ‘hundred square’. Many such games are freely available in books and on the internet. The activities in this unit come from NRICH, a free mathematical resources website that is part of the University of Cambridge’s (UK) Millennium Mathematics Project.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all, or at least part, of the activities yourself. It would be even better if you could try them out with a colleague as that will help you when you reflect on the experience. Trying them for yourself will mean you get insights into a learner’s experiences which can, in turn, influence your teaching and your experiences as a teacher.
Activity 1: What do you need?
For this activity, students work in pairs or small groups. You can use Resource 2, ‘Managing groupwork’, to help you prepare for the activity.
Give students a printout or copy of a hundred square (Figure 1), or make them use one they already have in their books. Make sure they can all see the hundred square. It is also important not to tell them how to go about doing this task but to let them discover it for themselves so they have to think about strategies. This also keeps up the suspense.
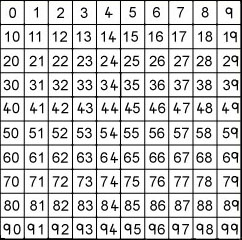
Part 1: Deciding on what you need to know
Write the following on the blackboard:
Eight clues
- The number is greater than 9.
- The number is not a multiple of 10.
- The number is a multiple of 7.
- The number is odd.
- The number is not a multiple of 11.
- The number is less than 200.
- Its ones digit is larger than its tens digit.
- Its tens digit is odd.
Tell the students the following:
I have got a number in my mind that is on the hundred square but I am not going to tell you what it is. However, you can ask me four of the eight clues that are written on the blackboard and I will answer with yes or no.
There is something else I need to tell you: four of the given clues are true but do nothing to help in finding the number. Four of the clues are necessary for finding it.
Can you find out, in your group, the four clues that help and the four clues that do not help in finding the number I am thinking of? What is it that you need to know to find a chosen number from your hundred square?
Part 2: What is the number?
This part is to test the students’ conjectures about what they found out in part 1 of the activity.
- Say to the students: ‘I am thinking of a number – in your groups, decide on four clues to ask me to find out what number I am thinking of.’
- After a few minutes ask one group for their clues and try them out. Whether they work or not, ask for the reason they chose those four clues. Ask if a group has a different set of clues and try those out. Stop when the clues work and discover your chosen number.
- Repeat this for several different numbers, or ask a student to take over your role and think of a number.
- Follow this with a discussion of which four clues are not needed to find the number, and why this is. What makes the best clues, and why?
(Source: adapted from NRICH, http://nrich.maths.org/ 5950.)
Video: Using local resources |
Case Study 1: Mrs Bhatia reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with her elementary students
I do agree that games are fun activities to do but I am always a bit sceptical when it is claimed they can offer rich opportunities for learning mathematics. I found it hard to believe that these number games could supplement the learning that happens in the normal traditional teaching I do in my classroom, when I explain mathematical ideas clearly to my students. But I decided to give it a go because I do find that even my younger students seem bored at times when doing mathematics, and that saddens me and makes me feel I have to try something else.
My class is large – about 80 students. Although they are supposed to be only from Classes III and IV, the attainment between the students varies a lot: some of the students seem to still struggle with early-year concepts of numbers, others are happy and able to do the work of higher classes. Finding activities that all of them can do and that challenge them all is very hard.
As I do not have access to resources such as a photocopier or large sheets of paper or scales for all students, in preparation for this activity I asked the students to draw a hundred square on the inside cover of their exercise books for homework. Most of the students had already done this, but some had not. I did not want to spend any time in the lesson letting those students draw one there and then so I made sure that when the students went into groups of four or five they were sat right next to someone who had done the homework so they could both look at the same hundred square. To move them into groups I simply asked the odd rows of students to turn around and work with the students sitting opposite them.
I was very uncomfortable with not giving the students precise instructions on how to go about finding out which clues were necessary or not, or to discuss this with the whole class first. I was really worried they would not know what to do. But I thought I would try and see if the activity would work and presented the task in the way it was described.
I decided that if the students still did not know how to proceed after four minutes, I would tell them. It did not take them that long. To make sure they were on-task I walked through the classroom and listened in on their discussions. I asked some of the groups ‘How will you find out?’ Their answers varied in the choice of numbers they would try the clues with, and their rationale for why to pick those. I noticed that neighbouring groups would listen to their replies as well, sometimes changing their approaches. In that way they all learned from each other without having to stop the whole class to discuss this.
I really liked the buzz in the class – there was excitement and engagement. The students were smiling a lot and developing their mathematical arguments to discuss, agree and disagree with each other. Everyone seemed to have a point to make and seemed to be included in the work of the groups.
After a while I told them they had three more minutes to decide on the clues, and that they had to make sure that everyone in their group knew and understood what the agreed clues were. I asked that because I wanted to make sure that all students in the group, whatever their attainment, would learn from this game. For this reason I also did not ask the ‘smartest’ student of the group the questions in the second part of the activity.
The discussion about why the clues were needed or not needed gave the students the opportunity to talk about their ideas. Sometimes, at the first go, they expressed themselves clumsily, but I then asked them to ‘say that again’, and I was amazed by how quickly most of them managed to express themselves more fluently the second time round. To make sure that not only the ‘smartest’ students answered I asked any student whether they agreed with what was said and insisted on them repeating the statement in their own words if they did. If they did not agree, they had to say why.
Reflecting on your teaching practice
When you do such an exercise with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and being able to progress, and those you needed to clarify. Such reflection always helps with finding a ‘script’ that helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Do this reflective exercise every time you undertake the activities, noting, as Mrs Bhatia did some of the smaller things that made a difference.
Pause for thought Good questions to trigger reflection are:
|
2 Essential characteristics of good games for mathematical learning
There are plenty of number games to be found in books and on the internet, but are they all good and effective for learning mathematics? To help in deciding which games offer good mathematical learning for use in the classroom it is helpful to first think about the characteristics of good educational games in general. Gough (1999) identified that a good game needs:
- an element of competitiveness; this can be achieved by having two or more players who take turns to achieve a ‘winning’ situation of some kind
- an element of choice and decision making about the next move throughout the game
- an element of interaction between the players in that the moves of one player affect the others.
Activity 2 presents some games that help to develop an understanding of number relationships. Many such games can be found freely in books and on the internet. Activities 1, 2 and 4 of this unit are adapted from the NRICH mathematical resources website.
Activity 2: Being strategic about numbers
Preparation
This game asks the students to think about place value and is enjoyed by students of all ages. For younger students the size of the boxes can be reduced.
Several variations to the game set-up and scoring systems are suggested. Once the students understand the set-up you can also ask them to come up with more variations and scoring systems of their own, as these will also require mathematical thinking.
For this activity students will need six-, nine- or ten-sided dice (with numbers 1 to 6, 1 to 9 or 1 to 10) or spinners with ten segments numbered 1 to 10 or 0. You can find templates for spinners in Resource 3 These resources can be used again in Activity 4.
Game 1 below describes how to set up the basic game, and Games 2 to 6 describe variations and developments from Game 1.
Playing the games
Game 1
This game is best played in pairs, or with two pairs playing against each other.
Each player draws a set of four boxes, as shown in Figure 2.

Instruct the students as follows:
- Take turns to roll the dice, read the number and decide which of your four boxes to fill with that number. Do this four times each until all your boxes are full. Read the four digits as a whole number
Whoever has the larger four-digit number wins.
Here are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Work out the difference between the two four-digit numbers after each round.
The winner keeps this score. First to 10,000 wins.
Game 2
Whoever makes the smaller four digit number wins.
You’ll probably want to change the scoring system from Game 1.
Game 3
Set a target to aim for. Then the students throw the dice four times each and work out how far each of them is from the target number. Whoever is the closer to the target number wins.
Here are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Work out the difference between the two four-digit numbers and the target number after each round. Keep a running total. First to 10,000 loses.
Game 4
This game introduces a decimal point. The decimal point will take up one of the cells so this time the dice only needs to be thrown three times by each player. Choose a target number. The winner is the one closest to the target.
Two possible versions:
- Each player decides in advance where they want to put the decimal point before taking turns to throw the dice.
- Each player throws the dice three times and then decides where to place the digits and the decimal point.
Again, different scoring systems are possible.
Game 5
This game really requires strategic thinking and can be very competitive! Tell your students the following:
Play any of the games above. This time you can choose to keep your number and put it in one of your cells, or give it to your partner and tell them which cell to put it in. It’s really important to take turns to start each round if this game is going to be fair.
This variation of the game becomes even more challenging when you play it with more than two people.
Game 6
This is a cooperative game rather than a competitive one – to be played by three or more people.
Tell your students the following:
- Choose any of the games above. Decide in advance which of you will get the closest to the target, who will be second closest, third, fourth, etc.
- Now work together to decide in whose cells the numbers should be placed, and where.
(Source: adapted from NRICH, http://nrich.maths.org/ 6605.)
Video: Planning lessons |
Case Study 2: Mr Mehta reflects on using Activity 2
From reading through the instructions for this activity I could see some of the learning opportunities it could offer, but I was not sure to what extent this would be a ‘good’ game. I discussed this with a colleague and we decided to first try it out ourselves in the staff room. And oh my, is it fun to play! We could hardly stop, and other teachers had a go as well.
I was a little bit worried about making up teams of younger and older students as I teach mixed-age groups, so when we first played the game I made students of similar age play in pairs against each other. We played game 1 and then game 2, each one a couple of times. Since then we have used these and other games regularly, sometimes at the beginning of the lesson to energise the students (especially good after lunch), and sometimes at the end of the lesson. It also works well as a reward, telling the students if they finish their work quickly we can play ‘being number strategists’.
I have used game 6, the ‘cooperative’ version of the game, with mixed-age groups and it is lovely to see how most of the older students support the younger ones. I initially thought it would help the older ones in their learning because they would have to help and communicate their mathematical thoughts with the younger students, and that has indeed been the case. At the same time I realised I made the assumption that the younger ones would be reluctant to talk with the older students – but that has proved wrong! The younger students are very happy arguing with the older ones about the mathematics involved.
Because we do not have dice in the school, I made the spinners myself. I made them on cardboard and they have now been used often, so it was worth the effort. I would like to make one big dice that I can roll and then all the students would have to work with the same numbers – just as a variation on the game.
It was good to read about the characteristics of a ‘good’ game. I had never really thought about it in detail. From watching the students play I think that much of the excitement and thinking that happens comes from having ‘an element of choice and decision making about the next move throughout the game’. And the characteristic of ‘an element of interaction between the players in that the moves of one player affects the other players’ seems to trigger them into strategic thinking behaviour – thinking beyond the next step. This strategic thinking really helped them to develop their understanding of place value because they had to think very carefully about the value of each digit.
Pause for thought In the case study, Mr Mehta was positive about the interaction between the older and younger students in his class. What strategies might he have used to support the students’ learning if the younger students had been more reluctant to talk or the older children had dominated the discussion? Reflect about how your own lesson(s) went using some of these questions:
Make some notes of your thoughts and ideas in response to these questions and discuss them with the teachers in your school or at a cluster meeting. |
3 Identifying the mathematical learning opportunities of number games
As stated at the beginning of this unit, playing number games can be beneficial for developing good social interaction, thinking and problem-solving skills, and can provide motivation for learning.
The games used so far in this unit have offered mathematical learning opportunities – that is, the games helped the students to develop their understanding of specific mathematical concepts and ideas – in this case, number sense. This means that games are not only fun for the students but are also a valid way to learn mathematics.
For example, in Activity 2 the mathematical learning opportunities for the students can be described as:
- learning about place value
- learning about the magnitude of numbers
- learning to use mathematical operations efficiently and accurately
- learning to work with numbers flexibly and fluidly.
Learning about these mathematical ideas is of considerable importance in the curriculum and essential for developing number sense.
The next activity builds on the game in Activity 2. The learning opportunities are extended to working with different operations, understanding number relationships and the effect of different mathematical operations on numbers.
Activity 3: Grid games
Preparation
This series of games follows on from the game ‘Being strategic about numbers’ in Activity 2.
Again there are several variations to choose from. These games are best played in pairs, or with two pairs playing against each other.
For this activity students will again need six-, nine- or ten-sided dice (with numbers 1 to 6, 1 to 9 or 1 to 10), or spinners with ten segments numbered 1 to 10 or 0. You can find templates for spinners in Resource 3.
Instructions for all games
Students take turns to throw the dice (or turn the spinner) and decide which of their cells on the grids to fill in.
This can be done in one of two ways: either fill in each cell as you throw the dice, or collect all your numbers and then decide where to place them.
Playing the games
Game 1
Each of the students draws an addition grid like Figure 3.
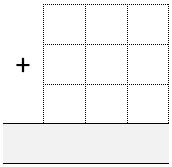
Throw the dice nine times each until all the cells are full.
Whoever has the sum closest to 1,000 wins.
There are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Each player keeps a running total of their ‘penalty points’, which is the difference between their result and 1,000 after each round. First to 5,000 loses.
You can vary the target to make it easier or more difficult, or you can get the class to practise using negative numbers (above 1,000 positive, below 1,000 negative) and suggest that the team closest to zero after ten rounds wins.
Game 2
Each of the students draws a subtraction grid like Figure 4.
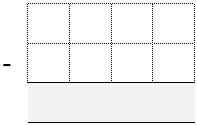
Throw the dice eight times each until all the cells are full.
Whoever has the difference closest to 1,000 wins.
Here are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Each player keeps a running total of their ‘penalty points’, which is the difference between their result and 1,000 after each round. First to 5,000 loses.
You can vary the target to make it easier or more difficult, perhaps including negative numbers as your target.
Game 3
Each of the students draws a multiplication grid like Figure 5.
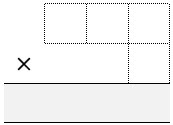
Throw the dice four times each until all the cells are full.
Whoever has the product closest to 1,000 wins.
Here are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Each player keeps a running total of their ‘penalty points’, which is the difference between their result and 1,000 after each round. First to 5,000 loses.
You can vary the target to make it easier or more difficult.
Game 4
Each of the students draws a multiplication grid like Figure 6.
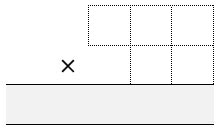
Throw the dice five times each until all the cells are full.
Whoever has the difference closest to 1,000 wins.
Here are two possible scoring systems:
- One point for a win. The first person to reach 10 points wins the game.
- Each player keeps a running total of their ‘penalty points’, which is the difference between their result and 1,000 after each round. First to 5,000 loses.
You can vary the target to make it easier or more difficult, perhaps including negative numbers as your target.
Game 5
You could introduce a decimal point and play any of the games above. The decimal point could take up one of the cells, so the dice would only need to be thrown four times by each player. You will need to decide on an appropriate target.
(Source: adapted from NRICH, http://nrich.maths.org/ 6606.)
Case Study 3: Mrs Mehta reflects on using Activity 3
I have used these different games now in a number of lessons, and with various classes. What I like about them are that the students really get engaged with and practise their sums a lot. The competitiveness and rules of the game make them talk and think strategically. They really think about place value, the magnitude of numbers and the effect of different mathematical operations on numbers. It works for younger and older students.
Sometimes I tell the students which game or operation I want them to use, at other times I let them choose for themselves. Initially, I had thought that the younger or lower-attaining students would stick to what they felt comfortable with doing. But that has proved not to be the case: sometimes they do stay in their comfort zone, but often they really push themselves and go for sums which I would personally never have given them.
I also like that it is self-correcting. Of course mistakes in calculations are made, but they check each other and tell each other when they do not agree. I think playing in pairs against each other helps with that. On the other hand, sometimes I really do think they have to do it for themselves, so I let them play one against one.
I now use these kinds of number games regularly instead of doing lots of practice. I do think they make the students think more about what they are doing mathematically. I have not used these number games yet instead of my normal way of teaching, but I am slowly getting convinced that perhaps I should give that a go because I have realised that all the students have some knowledge of doing sums – no doubt also a lot of misconceptions – but perhaps by using games I might find out what these misconceptions are exactly, and then plan my teaching to address these.
Pause for thought
|
4 Summary
This unit has focused on developing number sense in the elementary classroom by using games that offer rich mathematical learning opportunities.
In studying this unit you have thought about how using number games as a teaching strategy can stimulate engagement, participation and mathematical reasoning. You have considered how to adapt activities to different age groups and levels of attainment by making small changes such as changing the numbers or using different groupings.
Pause for thought Identify three opportunities in your lessons when you will use some of the ideas from this unit. |
Resources
Resource 1: NCF/NCFTE teaching requirements
This unit links to the following teaching requirements of the NCF (2005) and NCFTE (2009) and will help you to meet those requirements:
- Learn through activities that allow students to explore the properties of numbers.
- View students as active participants in their own learning encouraging their capacity to construct knowledge.
- Let students see mathematics as something to talk about, to communicate through, to share one’s finding, to discuss among them, and to work together on.
- Let students experience success in doing mathematical activities.
Resource 2: Managing groupwork
You can set up routines and rules to manage good groupwork. When you use groupwork regularly, students will know what you expect and find it enjoyable. Initially it is a good idea to work with your class to identify the benefits of working together in teams and groups. You should discuss what makes good groupwork behaviour and possibly generate a list of ‘rules’ that might be displayed; for example, ‘Respect for each other’, ‘Listening’, ‘Helping each other’, ‘Trying more than one idea’, etc.
It is important to give clear verbal instructions about the groupwork that can also be written on the blackboard for reference. You need to:
- direct your students to the groups they will work in according to your plan, perhaps designating areas in the classroom where they will work or giving instructions about moving any furniture or school bags
- be very clear about the task and write it on the board in short instructions or pictures. Allow your students to ask questions before you start.
During the lesson, move around to observe and check how the groups are doing. Offer advice where needed if they are deviating from the task or getting stuck.
At the end of the task, summarise what has been learnt and correct any misunderstandings that you have seen. You may want to hear feedback from each group, or ask just one or two groups who you think have some good ideas. Keep students’ reporting brief and encourage them to offer feedback on work from other groups by identifying what has been done well, what was interesting and what might be developed further.
Even if you want to adopt groupwork in your classroom, you may at times find it difficult to organize because some students:
- are resistant to active learning and do not engage
- are dominant
- do not participate due to poor interpersonal skills or lack of confidence.
To become effective at managing groupwork it is important to reflect on all the above points, in addition to considering how far the learning outcomes were met and how well your students responded (did they all benefit?). Consider and carefully plan any adjustments you might make to the group task, resources, timings or composition of the groups.
Resource 3: Templates for making spinners
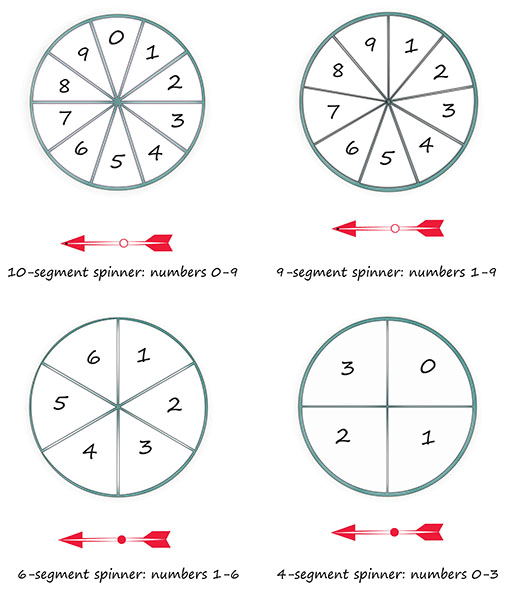
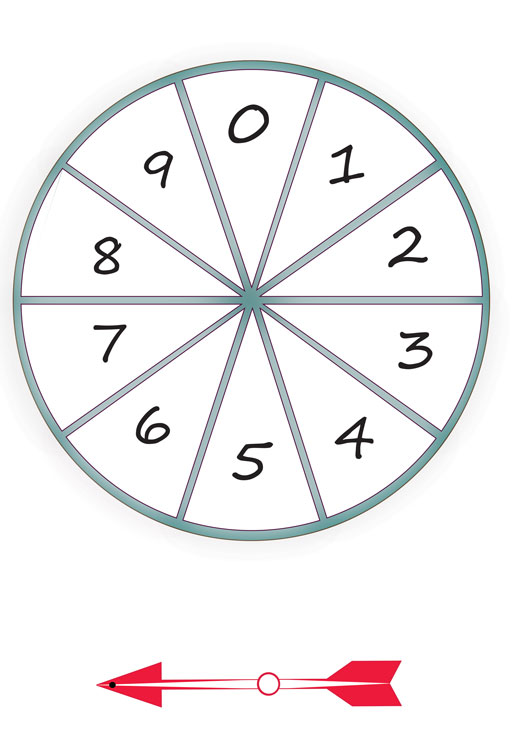
Additional resources
- ‘Number sense series: developing early number sense’ by Jenni Way: http://nrich.maths.org/ 2477
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- National Numeracy: http://www.nationalnumeracy.org.uk/ home/ index.html
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Math Playground’s logic games: http://www.mathplayground.com/ logicgames.html
- Maths is Fun: http://www.mathsisfun.com/
- Coolmath4kids.com: http://www.coolmath4kids.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- AMT-01 Aspects of Teaching Primary School Mathematics, Block 1 (‘Aspects of Teaching Mathematics’), Block 2 (‘Numbers (I)’), Block 3 (‘Numbers (II)’), Block 4 (‘Fractions’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-amt-01-study-materialbooks.html
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 4 (‘On Spatial Learning’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Manual of Mathematics Teaching Aids for Primary Schools, published by NCERT: http://www.arvindguptatoys.com/ arvindgupta/ pks-primarymanual.pdf
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Textbooks developed by the Eklavya Foundation with activity-based teaching mathematics at the primary level: http://www.eklavya.in/ pdfs/ Catalouge/ Eklavya_Catalogue_2012.pdf
- Central Board of Secondary Education’s books and support material (also including List of Hands-on Activities in Mathematics for Classes III to VIII) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
Except for third party materials and otherwise stated below, this content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/). The material acknowledged below is Proprietary and used under licence for this project, and not subject to the Creative Commons Licence. This means that this material may only be used unadapted within the TESS-India project and not in any subsequent OER versions. This includes the use of the TESS-India, OU and UKAID logos.
Grateful acknowledgement is made to the following sources for permission to reproduce the material in this unit:
Activity 1 and Figure 1: adapted from NRICH, http://nrich.maths.org/ 5950.
Activity 2 and Figure 2: adapted from NRICH, http://nrich.maths.org/ 6605.
Activity 3 and Figures 3–6: adapted from NRICH, http://nrich.maths.org/ 6606.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.