Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 3 May 2024, 2:28 PM
TI-AIE: Enacting vocabulary and asking questions: exploring the circle
What this unit is about
Circles are around us everywhere. The circle is a shape we rely on heavily in our lives: wheels are circles, as are dinner plates, cups, lids on bottles, DVDs and cogs in machinery. We also use the image of a circle in expressions such as ‘the circle of life’ and ‘going around in circles’. We sit in circles, eat circular chapattis and preserve food in circular tins; we also ride bicycles and drive cars with wheels. So we are all exposed to circles – working and playing with them, or talking about them – from an early age.
Students come to school with an intuitive understanding of circles and their properties. This unit will explore how to use that intuitive knowledge effectively by asking ‘good’ questions that help students notice the important mathematical ideas of variance and invariance. This will help your students to develop a better theoretical understanding of the concepts.
What you can learn in this unit
- How to build on your students’ intuitive understanding to develop a better understanding of the geometrical theory associated with circles.
- How to develop tasks to work on variance and invariance in circle geometry.
- Some suggestions of ‘good questions’ to ask your students to help them to notice and understand these mathematical concepts.
This unit links to the teaching requirements of the NCF (2005) and NCFTE (2009) as specified in Resource 1.
1 Intuitive learning
Learning about circles is part of learning about geometry. Geometry is often regarded as a part of the school mathematics curriculum that is difficult to understand and, as a result, can only be learned by memorisation.
This may seem surprising because life is full of geometry and we use it all the time and by doing so, develop an intuitive understanding of geometry. Byers and Herscovics describe intuitive understanding as ‘the ability to solve a problem without prior analysis of the problem’ (1977, p. 26).
So it should be possible to experience school geometry as an interesting, understandable and relevant subject area that relates to life experiences and builds on existing and often practical knowledge. There are barriers to achieving this, however.
Pause for thought Thinking of your own classroom, list three barriers to building on the intuitive understanding of your students to learn geometry. |
2 The circle in life versus the circle in mathematics: vocabulary
You can probably think of quite a few barriers to using intuitive learning in school geometry. This unit starts with one of them: how to make mathematical language more accessible and less reliant on ‘rote learning’ (memorisation).
A circle is a simple yet unique geometric shape. It has no vertices or corners, and all points on a circle are the same distance from the centre.
In order to explore geometry for Classes IX and X, students must become acquainted with new vocabulary in order to describe elements and concepts relating to the circle properly. (More activities around mathematics vocabulary can be found in the unit Building mathematical resilience: similarity and congruency in triangles.) This specific vocabulary is not much used outside of the mathematics classroom, and can therefore seem alien to students who may not know these words in the language that they use every day outside school. Often they have been asked to learn this vocabulary using rote learning. The vocabulary is shown in Figure 1.
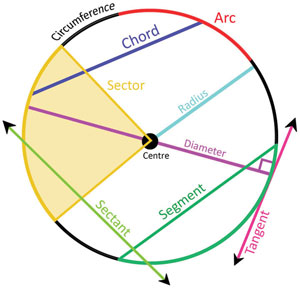
Note that the circumference of a circle means the length around it. It is a concept relating to calculations with the circle; therefore, is not an element of the circle as such.
Activity 1 aims to make students aware of the various terms that are used in relation to circles in a different way than simply learning the words by rote. It requires students to represent these terms and concepts physically and, in doing so, develop an image and a memory of them. The activity also asks students about variance and invariance: ‘What is the same?’ and ‘What is different?’, as well as ‘What has to stay the same?’ and ‘What can be changed?’ Working on invariance is a very useful teaching tool when learning geometry. Watson et al. (2013, p. 108) even claim that it:
is especially relevant and important in geometry. Most theorems in geometry can be seen as resulting from the study of what change is permitted that leaves some relationships or properties invariant.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.
Activity 1: Enacting the circle
For this activity, ask the students to sit in a circle (Figure 2). If your class is large, you might have 20–30 students in the circle and the other students watching. This activity will work best if you take your students outside, where there is more space. The activity is in two parts: the first is to give students instructions to move in certain ways; the second asks you to repeat the activity several times but with slight differences.

Part 1: Enacting terms associated with a circle
Instruct a student to move in certain ways to enact a term (how to do this is in the list below) but without telling them the name of the term. All students shout out to guess the name of the term. Then ask another student to describe how the term was enacted. To make the activity even more interactive, you could also ask students for their ideas on how they would enact the term.
Here is how the students could enact a term:
- Radius: Ask the student to get up, walk to the centre of the circle and then return to their position.
- Arc: Ask the student (S1) to name another student (S2); then ask S1, S2 and the fewer number of students sitting between S1 and S2 to raise their hands.
- Diameter: Ask the student (S1) to name the student sitting diametrically opposite to them (S2). Both students stretch their hands forward towards each other; alternatively, ask them to hold a piece of string between them.
- Chord: Ask the student to name any other student; both students stretch their hands toward each other or use string.
- Segment: Ask the student to name any other student; both students stretch their hands toward each other or use string. The fewer students sitting between the two students push their hands forward to fill in the gap.
- Sector: Ask the student to name any other student; both students move to the centre, shake hands and return to their positions.
- Circumference: Ask the student to get up and walk around the outside of the circle counting their steps aloud. The student then shouts out ‘the circumference of this circle is ... steps’.
Part 2: Building confidence with the vocabulary
This part of the activity builds on Part 1 and aims to give students the chance to become confident in naming each idea through repetition. During this part of the activity, students can also be encouraged to think about the properties of the terms and concepts in terms of variance and invariance (what can change and what cannot) by asking students questions such as the following:
- What is the same and what is different between (for example) an arc and a chord?
- Can you make another circumference?
- If you make another chord, what has to stay the same, and what can be changed?
Before the lesson you need to plan the questions you will ask the students. You can substitute the circle vocabulary in the questions above with other elements of circles.
Call the name of a student, and then name a term associated with circles that you want the student to enact. If the student cannot remember how to do it, ask whether anyone else remembers and can tell the student. After each student’s action, all students shout out the name of the term and another student describes how the term was enacted.
Repeat this several times, moving onto asking the variance and invariance questions.
At the end of the activity, tell you students to write a definition for each of the terms in their books. Then swap books and evaluate each other’s answers so that everyone has a record of good definitions.
You may also want to have a look at the key resource ‘Using questioning to promote thinking’.
Case Study 1: Mrs Chakrakodi reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with her secondary students.
It was a good exercise to encourage the students to get acquainted with the various terms involved in circles. They loved the enacting, although they were reluctant at first because we had not used similar activities before. I first gave them the instructions to enact the diameter and an arc. Before giving the next instruction, I asked them for their ideas on how to enact the term. At first this discussion was somewhat chaotic, because they were not really listening and building on each other’s ideas. So I asked them to first practise saying what they wanted to say with a partner. This worked really well and their ideas became really good, matching what was suggested in the activity.
The reaction to the questions about variance and invariance was amazing. It made all of us, including me, think differently about these terms and concepts: suddenly, the connections became clear, as did the role of certain elements of a circle such as the centre. Interestingly, after a while the students posed these questions without my intervention. So much better than simply learning the vocabulary by rote! This approach also showed the students that actually working on geometry does not need to be hard.
We then went in the classroom and worked on studying this vocabulary on paper. Students worked in groups of four and each group was assigned a different term or concept to prepare a presentation on what they had understood. This was then shared and other groups had to ask at least one question each. This way, each group tried to understand their own topic well and had to answer questions on it. They also had to listen to and understand what the others were saying, as well as ask questions. Their questions and answers showed that they were making connections between the topics.
Reflecting on your teaching practice
When you do such an exercise with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and being able to progress, and those where you needed to clarify. Such reflection always helps with finding a ‘script’ that helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting, as Mrs Chakrakodi did, some quite small things that made a difference.
Pause for thought Good questions to trigger reflection are:
|
3 Developing geometric intuition
Intuitive understanding of geometry develops from experiences in real life, and often involves dynamic images. The shapes we use and play with are not static: they change, they move and they can be transformed into other shapes. For example, when sharing a square piece of cake with a friend (equally of course!), the square can be transformed into two triangles, two rectangles, etc. When making rangoli patterns (see Figure 3), shapes within shapes are played with, changed and explored.

Similar playfulness with shapes can be found in architecture. In contrast, geometry in school mathematics is often perceived as something static: facts that are not possible to play with and change. In recent years that perception is slowly being addressed by the development of dynamic geometry software such as Cabri or the free shareware package GeoGebra.
So in addition to exploring ways to overcome the barrier of the language used in school geometry, you are now going to think about developing geometric intuition. Fujita et al. (2004) describe geometric intuition as involving:
the skills to create and manipulate geometrical figures in the mind, to see geometrical properties, to relate images to concepts and theorems in geometry, and decide where and how to start when solving problems in geometry.
Like Part 2 of Activity 1, this will focus on variance and invariance; that is, on what stays the same and what can change. The next activity gives an example of how students could work more intuitively on geometrical statements and develop dynamic geometrical images in the mind at the same time. They will do this by thinking about the statement: ‘Equal chords of a circle subtend equal angles at the centre.’
Activity 2: An intuitive approach to thinking about geometrical statements
For this activity, students need three straight long sticks such as bamboo poles, which are not the same length. Ask them to use these sticks to create a triangular frame so that two of the sides of the frame are equal – in other words, to create an isosceles triangle (see Figure 4). This activity is best done outside, if possible, where the students can trace their movements in some soil or sand.

Part 1: Seeing what is happening
- Ask each of the students holding the bamboo poles to say something about the sticks (or sides of the triangle) that they are holding. Can they say something about the angle or relative length? What is the same as and what is different from the other sides or angles?
- Now ask the students to move the sides of the triangle. Tell Student 1 to stay in the same position, although they can turn. Ask Students 2 and 3 to move the triangle, leaving Student 1 in the same place.
- Ask the other students the following questions:
- What shape is formed when tracing the movements of Student 2, then Student 3? (Answer: a circle – and both students are forming the same circle.)
- Why is this shape formed?
- What role is Student 1 enacting? (Answer: the centre of the circle.)
- How they could describe the distance between Students 2 and 3? (Answer: a chord of the circle.)
- How they could describe the distance between Students 1 and 2 or Students 1 and 3? (Answer: the radius.)
Part 2: Working on invariance
Ask the students first to discuss in threes and be ready to share their thinking about these three questions with the rest of the class:
- In what ways could the length of the bamboo sticks be changed?
- What else would change in these cases? What would stay the same?
- Can they make a mathematical statement that would describe what they think?
Part 3: Making sense of the mathematical statement ‘Equal chords of a circle subtend equal angles at the centre’
While still outside, give the students the statement ‘Equal chords of a circle subtend equal angles at the centre’ in some written format, because it is very difficult to remember.
- Ask the students to discuss in groups of three what this statement could mean. How does it relate to what they have been working on? Remind them they can try it out by using the bamboo sticks or in some other way.
- Ask the students for suggestions on how such mathematical statements could be made more accessible.
- Have a whole-class discussion about their thoughts.
You can read more in Resource 2, ‘Using local resources’.
Case Study 2: Mrs Chakrakodi reflects on using Activity 2
For this activity we went out in the field. First we did Part 1 together as a whole class. Because I had enough bamboo sticks for five groups, I divided the students into five groups and gave them three pieces of bamboo, two of which were of the same length, and one that was different for each group. They were then told to do Part 1 of the activity within their groups and mark out the path it made. I also asked them to make notes of their observations.
The third stick of each group was then exchanged several times (they were all of different lengths) and they did the same activity again. I decided to do this before asking the questions from Part 2 of the activity, because I thought this might lead them to actually come up with similar questions. Then by the time I asked them the questions of Part 2, they would feel good, as it would be questions they had thought of already – which indeed was the case to some extent.
For Part 2 I asked them to work in groups of three at first because I thought working in smaller groups would help the mathematical discussion. They found making mathematical statements hard, but they had a go at it. It provided good preparation for Part 3 of the activity. To make sense of the vocabulary of the statement ‘Equal chords of a circle subtend equal angles at the centre’, it was really helpful to do that part of the activity in the same physical setting because it allowed the students to really point to what they had done earlier, try out some ideas and relate their vocabulary to that of the given statement.
There was a lot of running around and movement. After they had all noted down what they observed and had some whole-group discussions, we went back to the classroom. Once there, they sat down to have a further discussion of what had happened and what it meant. Although some part of that discussion repeated what was said earlier, I thought it important to make the link explicit between what happened outside the classroom and what they had to do sitting in their desks, surrounded by textbooks and exercise books. As part of their home activity I asked them to think of some activity for the other properties they had already discussed in Activity 1.
Pause for thought
|
4 Making up own questions to develop geometric imagery
Activity 2 and Case Study 2 illustrate how school geometry can be learned by working on the intuitive knowledge that students have. Mrs Chakrakodi described how he reinforced the link between what was learned outside and inside the classroom through discussions. By studying geometry using sticks and asking students to ‘enact’ the movement, time and time again, images are formed in their minds. These images are important for developing the geometric intuition described earlier in this unit. It is also important to become aware that not all people will ‘see’ the same image when given a description.
A good way to ask students to engage with a geometrical image is to ask them what questions could be posed.
Activity 3: Asking good questions
This task works well for students working both individually and in pairs, followed by a whole-class discussion or a brainstorm, followed by more individual/paired work, and so on.
Ask the students to look at Figure 5 and come up with possible questions about it.

Some of the questions could be:
- What is the centre of the circle?
- What is the point P?
- Why is the angle OTP a right angle?
- What is the line t?
- How is the line t related to the line t’?
Pause for thought
|
Guiding students to ask good questions is a technique that you can use in many different topics. It is an excellent technique for helping you to assess students’ understanding of the topic. When students have generated their questions, you can ask pairs to swap questions and try to answer each other’s questions. Then return the answers to be marked. When students are doing this type of activity it is important to walk round the room and listen to what they are saying – if students are not participating, you should encourage them. In the next lesson you might want to move students to work with different partners so that they can help each other.
5 Summary
This unit has discussed geometric ideas, particularly focusing on circles. The ideas are not complex in themselves, but you have been asked to think about some complex pedagogical ideas. First you were asked to think about asking the students to use circle vocabulary themselves in describing what they were enacting, rather than just to learn new words by rote. Students who use vocabulary themselves – especially to describe something they or their peers are doing – internalise the words naturally and remember them. Think now about another area of mathematics where it may help the students to remember better if they used and enacted the words themselves.
The other important pedagogical idea in this unit is the use of variance and invariance. Asking what is the same and what is different directs the students’ attention to important mathematical ideas. They can make connections or understand and generalise for themselves – something else that helps students make the ideas their own and easy to draw on, control and use in unfamiliar contexts.
Pause for thought Identify three ideas that you have used in this unit that would work when teaching other topics. Make a note now of two topics you have to teach soon where those ideas can be used with some small adjustments. |
Resources
Resource 1: NCF/NCFTE teaching requirements
This unit links to the following teaching requirements of the NCF (2005) and NCFTE (2009), and will help you to meet those requirements:
- View learners as active participants in their own learning and not as mere recipients of knowledge; to encourage their capacity to construct knowledge; to ensure that learning shifts away from rote methods.
- View learning as a search for meaning out of personal experiences and knowledge generation as a continuously evolving process of reflective learning.
- Support students to learn to enjoy mathematics rather than fear it.
- Help students to see mathematics as something to talk about, to communicate through, to discuss among themselves, to work together on.
Resource 2: Using local resources
Many learning resources can be used in teaching – not just textbooks. If you offer ways to learn that use different senses (visual, auditory, touch, smell, taste), you will appeal to the different ways that students learn. There are resources all around you that you might use in your classroom, and that could support your students’ learning. Any school can generate its own learning resources at little or no cost. By sourcing these materials locally, connections are made between the curriculum and your students’ lives.
You will find people in your immediate environment who have expertise in a wide range of topics; you will also find a range of natural resources. This can help you to create links with the local community, demonstrate its value, stimulate students to see the richness and diversity of their environment, and perhaps most importantly work towards a holistic approach to student learning – that is, learning inside and outside the school.
Making the most of your classroom
People work hard at making their homes as attractive as possible. It is worth thinking about the environment that you expect your students to learn in. Anything you can do to make your classroom and school an attractive place to learn will have a positive impact on your students. There is plenty that you can do to make your classroom interesting and attractive for students – for example, you can:
- make posters from old magazines and brochures
- bring in objects and artefacts related to the current topic
- display your students’ work
- change the classroom displays to keep students curious and prompt new learning.
Using local experts in your classroom
If you are doing work on money or quantities in mathematics, you could invite market traders or dressmakers into the classroom to come to explain how they use maths in their work. Alternatively, if you are exploring patterns and shapes in art, you could invite maindi [wedding henna] designers to the school to explain the different shapes, designs, traditions and techniques. Inviting guests works best when the link with educational aims is clear to everyone and there are shared expectations of timing.
You may also have experts within the school community (such as the cook or the caretaker) who can be shadowed or interviewed by students related to their learning; for example, to find out about quantities used in cooking, or how weather conditions impact on the school grounds and buildings.
Using the outside environment
Outside your classroom there is a whole range of resources that you can use in your lessons. You could collect (or ask your class to collect) objects such as leaves, spiders, plants, insects, rocks or wood. Bringing these resources in can lead to interesting classroom displays that can be referred to in lessons. They can provide objects for discussion or experimentation such as an activity in classification, or living or not-living objects. There are also resources such as bus timetables or advertisements that might be readily available and relevant to your local community – these can be turned into learning resources by setting tasks to identify words, compare qualities or calculate journey times.
Objects from outside can be brought into the classroom – but the outside can also be an extension of your classroom. There is usually more room to move outside and for all students to see more easily. When you take your class outside to learn, they can do activities such as:
- estimating and measuring distances
- demonstrating that every point on a circle is the same distance from the central point
- recording the length of shadows at different times of the day
- reading signs and instructions
- conducting interviews and surveys
- locating solar panels
- monitoring crop growth and rainfall.
Outside, their learning is based on realities and their own experiences, and may be more transferable to other contexts.
If your work outside involves leaving the school premises, before you go you need to obtain the school leader’s permission, plan timings, check for safety and make rules clear to the students. You and your students should be clear about what is to be learnt before you depart.
Adapting resources
You may want to adapt existing resources to make them more appropriate to your students. These changes may be small but could make a big difference, especially if you are trying to make the learning relevant to all the students in the class. You might, for example, change place and people names if they relate to another state, or change the gender of a person in a song, or introduce a child with a disability into a story. In this way you can make the resources more inclusive and appropriate to your class and their learning.
Work with your colleagues to be resourceful: you will have a range of skills between you to generate and adapt resources. One colleague might have skills in music, another in puppet making or organising outdoor science. You can share the resources you use in your classroom with your colleagues to help you all generate a rich learning environment in all areas of your school.
Additional resources
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
Except for third party materials and otherwise stated below, this content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/). The material acknowledged below is Proprietary and used under licence for this project, and not subject to the Creative Commons Licence. This means that this material may only be used unadapted within the TESS-India project and not in any subsequent OER versions. This includes the use of the TESS-India, OU and UKAID logos.
Grateful acknowledgement is made to the following sources for permission to reproduce the material in this unit:
Figure 1: adapted from http://upload.wikimedia.org/ wikipedia/ commons/ thumb/ 4/ 4f/ Circle_slices.svg/ 500px-Circle_slices.svg.png.
Figure 2: © unknown
Figure 3: courtesy of http://www.thehindu.com/ todays-paper/ tp-national/ tp-karnataka/ the-road-doubled-up-as-their-canvas/ article699822.ece
Figure 4: adapted from https://commons.wikimedia.org/ wiki/ File:Thales%27_Theorem_Tangents.svg.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.