Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Saturday, 22 November 2025, 2:47 PM
TI-AIE: Developing creative thinking in mathematics: trigonometry
What this unit is about
Trigonometry plays a very important role in the Indian National Curriculum Framework (2005). It links concepts about shape and space with other mathematical ideas such as ratio, deduction and mathematical proof. It also provides an opportunity to link what is observed in real life with the world of the mathematics classroom.
Unfortunately, many students do not experience the richness, connections or creativity that trigonometry allows. Instead they often perceive it as another memory exercise where rules and formulae must be learnt ‘by rote’, along with methods for working out problems.
This unit aims to help you address these views by working on trigonometry in a playful and creative way, using the students’ mental thinking powers. The unit will show that if you make small changes to tasks, students will be able to learn more effectively. When students are allowed to make more choices and decisions themselves, they can enjoy trigonometry and feel empowered by their mathematics learning.
Pause for thought
|
What you can learn in this unit
- How to promote the use of mathematical terminology that supports the use of trigonometry.
- How to teach concepts and applications of trigonometry through activities that are creative and playful.
- Some ideas to support your students in developing problem solving methods that rely less on memorisation.
This unit links to the teaching requirements of the NCF (2005) and NCFTE (2009) outlined in Resource 1.
1 Creativity in learning mathematics
Creativity in learning has become a fashionable concept in recent years. Creativity is partly about allowing students to enjoy learning more and think for themselves. It is also important to prepare students for the jobs of the future. In the future, jobs will rely less and less on doing things mechanistically (as this can be done by computers) and more on problem solving, thinking outside the box and coming up with creative solutions.
It is not always easy to see how school mathematics and textbook practice can be turned into creative learning approaches. This unit aims to give some ideas in this direction. It builds on the perspective of creativity as ‘possibility thinking’ (Aristeidou, 2011), using ‘What if?’ scenarios.
Research has identified a list of teaching and learning features that are involved in possibility thinking in the classroom (Grainger et al., 2007; Craft et al., 2012). These include posing questions, experimenting with ideas, taking risks, playing around and working collaboratively.
The tasks in this unit work on these features.
Pause for thought Think about a time that you felt you have been creative in your thinking. It does not have to be about doing mathematics – it could, for example, be when you were cooking, doing a handicraft, solving a tricky problem at home or thinking about something. What happened? Was there, for example, any questioning, experimenting, playfulness, risk-taking or collaboration involved? |
2 The role of choice
Playfulness is considered important to support creativity because in play you explore many possible solutions in a spontaneous way. This is known as divergent thinking. The word ‘playfulness’ is often associated with young children, but should not be restricted to them. Play is about exploring and experimenting, which anyone of any age can do. Simply watching children play can be a good reminder of their creativity.
When they are exploring and experimenting, it is important that students have choices: the choice to approach a problem in different ways, the option to make mistakes or the choice to come up with their own conjectures and test whether they are valid or not. In Activity 1 you give students that choice by simply asking the question, ‘In how many ways can you …?’
The activity aims for students to become knowledgeable and confident that closed polygons can be divided into right-angled triangles. This will enable them to ‘just do it’ when they have to find right-angled triangles to use in trigonometry problems later, such as when proving the cosine rule. In that way, being able to play with right-angled triangles in a polygon can become a tool to ‘getting unstuck’ later.
This task works well for students first exploring possibilities on their own, and then discussing these with classmates or in groups to get more ideas and refine their thinking.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about the way that the activity went and the learning that happened. This will help you to develop a more learner-focused teaching environment.
Activity 1: Students investigate triangles in polygons
Ask your students the following:
- In how many ways can you divide each of the shapes in Figure 1 into right-angled triangles?
- Draw any right-angled triangle (Figure 2). What kind of closed polygons can you construct by using this triangle as a building block?

Figure 3 shows an example.

- Do you think that all closed polygons can be formed by right angled triangles? Give reasons to justify your answer.
- Why do you think this activity asks you to investigate whether any closed polygons can be made up of right-angled triangles?
You may also want to have a look at the key resource ‘Involving all’.
Case Study 1: Mrs Nagaraju reflects on using Activity 1
This is the account of a teacher who tried Activity 1 with her secondary students.
What really struck me was the enthusiasm of the students when doing this activity. I had not expected that. We read the first question of the task together and I then asked the students to work on their own for a while, because I wanted them to have the opportunity to think on their own first. They could discuss their ideas with their classmates when they felt ready.
Everyone got really busy trying to divide the given figure into right-angled triangles. Some started by dividing the figure into triangles that were not right-angled triangles; I decided not to interfere immediately, as I would normally do, but allow the students to make their own mistakes! I noticed that most of these students self-corrected: they glanced at other students’ work, read the question again and changed what they were doing. They did not lose their enthusiasm and continued with what seemed like new energy.
When some students had started discussing their ideas, I stopped the class and asked, ‘Why do you think it is important to work with right-angled triangles?’ I asked several of the students who had done it ‘wrong’ to talk about what they had experienced and what they thought. In this way, everyone in the class learned that making mistakes actually can offer very good learning opportunities.
They found making the closed polygons with right-angled triangles even more exciting, because they had the freedom to form figures of their own. Again, some students ended up making non-closed polygons but self-corrected. Gaurav made cut-outs of right-angled triangles and used these to compile different figures. Some were known geometric figures such as hexagons; others were more random formations and some were even figurines existing of several closed polygons. Students were interested in each other’s work and were inspired by what they saw their peers doing, and used similar approaches. Others used straight edges and a pencil to draw.
Look at Resource 2, ‘Monitoring and giving feedback’, for further information.
Reflecting on your teaching practice
When you do such an activity with your class, reflect afterwards on what went well and what went less well. Consider the questions that led to the students being interested and being able to get on and those where you needed to clarify. Such reflection always helps with finding a ‘script’ that helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting, as Mrs Nagaraju did, some quite small things that made a difference.
Pause for thought Good questions to trigger such reflection are:
|
3 Using the question ‘What happens if …?’
Activity 1 used the question ‘In how many ways …?’ to trigger students to play, explore and investigate how any closed polygons could be made up of right-angled triangles. Having the choice of how to go about this, and make mistakes, enthused your students to engage with the task.
Playfulness involves thinking about changes in situations. This is sometimes referred to as ‘What if?’ thinking. It works very well with thinking about variables in mathematics: ‘What will happen to the other variables when I change this variable?’ In this process of thinking of possibilities, the role of and connection between, variables and constants are also discovered.
Activity 2 asks students to think about asking ‘What happens if I change …?’ They can get a sense of ownership and feeling valued for their thinking powers from coming up with their own conjectures and by using their own examples to work on. At the end of the activity, collating information based on these different examples will also allow for generalisations to be made.
The activity also asks students to first think about what is going to happen before testing their ideas. This should help them to consider what thinking is required (called ‘meta-cognition’). When their thinking proves to be right, this can make them feel good because they get it ‘right’. If their conjectures prove incorrect, this can also surprise them and make them feel intrigued about ‘Why it is that …?’
Activity 2: Students discover asking ‘What happens if …?’
This activity requires your students to explore what happens if they change a side or angle of the triangle, and to consider the effect this change has on the other angles and sides.
Part 1
Tell your students the following:
- Draw a right-angled triangle and label it as in Figure 4.
Figure 4 An example of a right-angled triangle.
- In Table 1, each row indicates a transformation to a side or an angle of the triangle that you have drawn. The blank cells need to be completed with how the other parts of the triangle will increase or decrease as a result of the transformation.
- Make a copy of the table and first write down what you think will be the change; then check by drawing the changes. If there is no change, write ‘no change’.
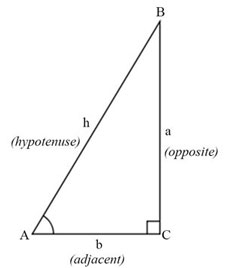
| Angle A | Angle B | Angle C | AB | BC | AC |
|---|---|---|---|---|---|
| Increases | Fixed | ||||
| Decreases | Fixed | ||||
| Increases | Fixed | ||||
| Decreases | Fixed | ||||
| Fixed | Doubled | ||||
| Fixed | Is halved | ||||
| Fixed | Increases | ||||
| Fixed | Fixed | ||||
| Fixed | Fixed |
- What do you notice? Why do you think this is?
Part 2
- In each row of Table 2, you are given the size of angle C and the lengths of sides AB (the hypotenuse) and AC.
- Draw these triangles and determine the values of other missing parts.
- Again, make a copy of the table and first write down what you think will happen, before checking by drawing the triangles.
| Angle A | Angle B | Angle C | Hypotenuse (AB) | a | AC |
|---|---|---|---|---|---|
| 90° | 2 | 1 | |||
| 90° | 4 | 2 | |||
| 90° | 6 | 3 | |||
| 90° | 8 | 4 |
- What do you notice? Why do you think this is?
Case Study 2: Mr Chadha reflects on using Activity 2
I introduced Part 1 of the activity by telling the students they were going to do a ‘What happens if …?’ problem that required them to be detectives and to think about possibilities. First of all they had to construct a right-angled triangle using their own measurements, which they had to first jot down. Having done that, I asked them to copy Table 1, which I had written on the blackboard.
At first they started to use the measurements of their own triangle to fill in the table and I had to remind them that they were looking for increases and decreases. This helped them to get started. I could see several of them moving their arms while squinting their eyes. When I asked Nitin what he was doing when he moved his arms, he said, ‘I am increasing the angle in my mind’s eye so I can “see” what happens to the other sides.’ I told him that was interesting and to carry on. When it came to thinking what happened to the other angles when the sides are doubled or halved, some students needed to draw the new triangle at least roughly so that they were certain. I encouraged them to ‘imagine’, to use pencils or to draw – whatever they chose to do – to ‘see’ what happens when a right-angled triangle is manipulated in this way.
Once the table was filled in, the students had to think about what they noticed. I first asked them to look at their table and think for 30 seconds; then I asked them to tell their partner what they thought they saw in the table and to agree on something that they noticed. I then asked the students to tell another pair what they had noticed and agree an idea in their group of four. Each group told the rest of the class what they had noticed and a lively discussion ensued. I felt that this made sure everyone’s ideas were discussed and included in a very short time.
Then we went on to Part 2. This time I asked them to fill in the table with what they thought would happen without any drawing at all – even in their mind’s eye! After giving them two or three minutes to do this, I asked them to work in pairs to do the drawing so that they could check what they thought was correct or not. Drawing is always difficult to do accurately, so I reminded them that the drawing was to make sure that what they thought in theory was actually the case. If they measured an angle and it seemed to be a few degrees out, I asked them to think whether it was their ‘theory’ that was likely to be ‘wrong’, or their ‘practice’. They quickly understood what I was saying and were able to argue for their own ‘theory’. I also heard several students say ‘I noticed that …’ as they were working so that they were ready for the class discussion that followed.
Pause for thought Think back about some of the features of possibility thinking from Section 1 of this unit and consider whether your students:
Which of your students especially displayed these skills? Can you give examples? |
4 Thinking beyond the doing

Figure 5 The Red Fort or Lal Qil'ah in Delhi.
Learning mathematics in school can result in students simply following procedures and not having to think why a certain algorithm of method is used, why it works or why it could give answers to questions.
The next activity is about working out the height of a tree, a tall object or a local landmark that is too high to measure with rules or ropes or anything else. You ask students to make a clinometer, which is a tool used by land surveyors to work out heights. Instead of being given a manual showing how to use it, the students are asked to design such a manual, so they will first have to work out by themselves how and why a clinometer is a suitable tool – and, as such, what the mathematics of using a clinometer is. They have to make decisions on how to go about it, what to write in the manual and how to express their mathematical explanation.
Activity 3: Students make a clinometer
Tell your students the following:
In this activity you are asked to make a clinometer. This is a tool to help surveyors measure the height of tall structures such as trees, landmarks or buildings. You are then asked to imagine you work for a company that produces such clinometers and you have to write a manual on how to use it. Remember that your clients are surveyors who are quite knowledgeable about mathematics and trigonometry, so feel free to include mathematical explanations on how and why a clinometer can be used for working out heights.
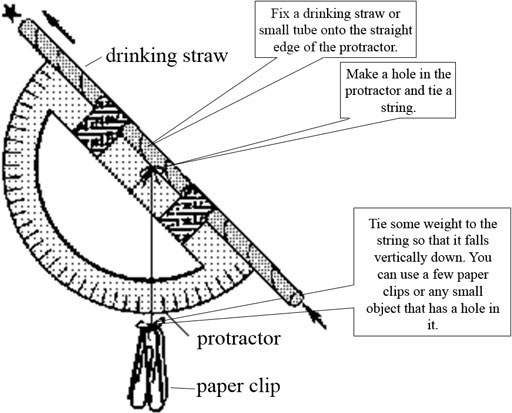
To make a clinometer you will first need to modify your protractor and use it as shown in Figures 6 and 7.
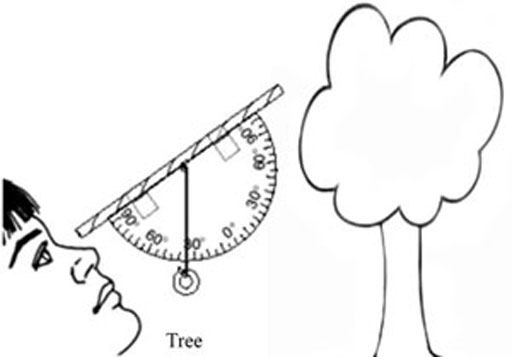
The clinometer measures what is called the ‘angle of elevation’ and you use it as shown in Figure 7.
Answer these questions to help you design your manual:
- What are the components of this instrument and how does it work? What is the mathematics involved? It might help to make a drawing of what you think happens.
- Work out how you can use your clinometer to work out the heights of a tall object. What is the mathematics involved? It might help to draw what you think happens.
- What happens if you stand on a hill and the object you are measuring is at the top of the hill? Do you need a different method or not?
- Write your manual to explain to its users how the clinometer works and how to use it. Remember that drawings might make it clearer.
Case Study 3: Mrs Meganathan reflects on using Activity 3
At the start I felt unsure about using this task. Normally the tasks are broken down into small activities or exercises, guiding the students what to do step-by-step. This task seemed so unstructured in comparison!
I decided to tell the students my concern about this task being less structured compared with the usual problems we use in class and that I thought they might need more guidance and steps. Well, perhaps they took that as a challenge, but they took to the task with enthusiasm and determination. They worked in pairs and groups of three. We introduced a short feedback session every 10–15 minutes or so, to share ideas and discuss issues and observations, and to put my mind at rest that the students were coping well with this less structured task.
We first worked on the task in the classroom, thinking about heights to the top of the blackboard, the light and the height of the classroom. When they had developed their theories about how the clinometer worked we went outside, took rope and tape measures and tried to work out the heights of the school, some trees and the distance to a window on the first floor. Comparing the calculations between the groups made the students consider their methods, the accuracy of their calculations and the precision of their measurement. The students really enjoyed putting together their manual and volunteered to take it home to finish.
This task also made me think about breaking down problems in step-by-step instructions. I now think I might not be doing the students any favours or supporting their learning or thinking in these step-by-step tasks: it tells them what to do and how to think, so there is little choice or opportunity for creativity. I am not sure I will be able to turn these step-by-step tasks into more unstructured tasks, but I will make a start by perhaps removing some of the steps, removing a given table, etc., so that the students have to figure that out for themselves.
Pause for thought How did it go with your class? What questions did you use to probe your students’ understanding? Did you feel you had to intervene at any point? What points did you feel you had to reinforce? Did you modify the task in any way like Mrs Meganathan did? If so, what was your reasoning for this? |
5 Summary
This unit has discussed some ideas associated with trigonometry, but its chief focus has been on creativity and allowing the students to think ‘What happens if …?’, or to engage in ‘possibility’ thinking. Possibility thinking asks students to be creative, to try things out and make their own decisions – and therefore their own mistakes.
Teachers sometimes think it is their job to prevent their students from making mistakes. This unit demonstrates that it is the teacher’s job to allow the students to make mistakes and to learn from them. Asking the students to ‘play with ideas’ means that they exercise their creative side, try out lots of ideas and so, end up really knowing and understanding what they have learned.
Asking your students to be creative and playful, and to make choices for themselves, also means that they are better placed when asked about something in an unfamiliar context, as often happens in examinations. They know that if they think around an idea and try some things out, they can solve a problem that looks difficult to begin with – just as they have done before.
Pause for thought Identify three ideas that you have used in this unit that would work when teaching other topics. Make a note now of two topics you have to teach soon where those ideas can be used with some small adjustments. |
Resources
Resource 1: NCF/NCFTE teaching requirements
The learning in this unit links to the NCF (2005) and NCFTE (2009) teaching requirements as specified below:
- View learners as active participants in their own learning and not as mere recipients of knowledge; to encourage their capacity to construct knowledge; to ensure that learning shifts away from rote methods.
- View learning as a search for meaning out of personal experiences and knowledge generation as a continuously evolving process of reflective learning.
- Support students to learn to enjoy mathematics rather than fear it.
- Connect school knowledge with community knowledge and life outside the school.
Resource 2: Monitoring and giving feedback
Improving students’ performance involves constantly monitoring and responding to them, so that they know what is expected of them and they get feedback after completing tasks. They can improve their performance through your constructive feedback.
Monitoring
Effective teachers monitor their students most of the time. Generally, most teachers monitor their students’ work by listening and observing what they do in class. Monitoring students’ progress is critical because it helps them to:
- achieve higher grades
- be more aware of their performance and more responsible for their learning
- improve their learning
- predict achievement on state and local standardised tests.
It will also help you as a teacher to decide:
- when to ask a question or give a prompt
- when to praise
- whether to challenge
- how to include different groups of students in a task
- what to do about mistakes.
Students improve most when they are given clear and prompt feedback on their progress. Using monitoring will enable you to give regular feedback, letting your students know how they are doing and what else they need to do to advance their learning.
One of the challenges you will face is helping students to set their own learning targets, also known as self-monitoring. Students, especially struggling ones, are not used to having ownership of their own learning. But you can help any student to set their own targets or goals for a project, plan out their work and set deadlines, and self- monitor their progress. Practising the process and mastering the skill of self-monitoring will serve them well in school and throughout their lives.
Listening to and observing students
Most of the time, listening to and observing students is done naturally by teachers; it is a simple monitoring tool. For example, you may:
- listen to your students reading aloud
- listen to discussions in pair or groupwork
- observe students using resources outdoors or in the classroom
- observe the body language of groups as they work.
Make sure that the observations you collect are true evidence of student learning or progress. Only document what you can see, hear, justify or count.
As students work, move around the classroom in order to make brief observation notes. You can use a class list to record which students need more help, and also to note any emerging misunderstandings. You can use these observations and notes to give feedback to the whole class or prompt and encourage groups or individuals.
Giving feedback
Feedback is information that you give to a student about how they have performed in relation to a stated goal or expected outcome. Effective feedback provides the student with:
- information about what happened
- an evaluation of how well the action or task was performed
- guidance as to how their performance can be improved.
When you give feedback to each student, it should help them to know:
- what they can actually do
- what they cannot do yet
- how their work compares with that of others
- how they can improve.
It is important to remember that effective feedback helps students. You do not want to inhibit learning because your feedback is unclear or unfair. Effective feedback is:
- focused on the task being undertaken and the learning that the student needs to do
- clear and honest, telling the student what is good about their learning as well as what requires improvement
- actionable, telling the student to do something that they are able to do
- given in appropriate language that the student can understand
- given at the right time – if it’s given too soon, the student will think ‘I was just going to do that!’; too late, and the student’s focus will have moved elsewhere and they will not want to go back and do what is asked.
Whether feedback is spoken or written in the students’ workbooks, it becomes more effective if it follows the guidelines given below.
Using praise and positive language
When we are praised and encouraged, we generally feel a great deal better than when we are criticised or corrected. Reinforcement and positive language is motivating for the whole class and for individuals of all ages. Remember that praise must be specific and targeted on the work done rather than about the student themselves, otherwise it will not help the student progress. ‘Well done’ is non-specific, so it is better to say one of the following:
Using prompting as well as correction
The dialogue that you have with your students helps their learning. If you tell them that an answer is incorrect and finish the dialogue there, you miss the opportunity to help them to keep thinking and trying for themselves. If you give students a hint or ask them a further question, you prompt them to think more deeply and encourage them to find answers and take responsibility for their own learning. For example, you can encourage a better answer or prompt a different angle on a problem by saying such things as:
It may be appropriate to encourage other students to help each other. You can do this by opening your questions to the rest of the class with such comments as:
Correcting students with a ‘yes’ or ‘no’ might be appropriate to tasks such as spelling or number practice, but even here you can prompt students to look for emerging patterns in their answers, make connections with similar answers or open a discussion about why a certain answer is incorrect.
Self-correction and peer correction is effective and you can encourage this by asking students to check their own and each other’s work while doing tasks or assignments in pairs. It is best to focus on one aspect to correct at a time so that there is not too much confusing information.
Additional resources
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
Except for third party materials and otherwise stated below, this content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/). The material acknowledged below is Proprietary and used under licence for this project, and not subject to the Creative Commons Licence. This means that this material may only be used unadapted within the TESS-India project and not in any subsequent OER versions. This includes the use of the TESS-India, OU and UKAID logos.
Grateful acknowledgement is made to the following sources for permission to reproduce the material in this unit:
Figure 5: photo of the Red Fort or Lal Qil'ah in Delhi courtesy of Clare Lee.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.