Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Saturday, 22 November 2025, 8:59 AM
TI-AIE: Developing mathematical reasoning: mathematical proof
What this unit is about
Mathematical proof is often considered to be one of the cornerstones of mathematics. Professional mathematicians spend a lot of time developing conjectures and then working on whether they hold true for all cases, for some or for none. Proofs and justifications have to be rigorous and based on known mathematical facts and properties. Understanding and knowledge of mathematics is examined and extended in this process of proving, and connections across mathematical ideas and concepts are made.
Proving can also be an excellent activity to undertake in the classroom to develop an understanding of mathematics, engaging students in activities undertaken by real mathematicians. But often in school mathematics, proof is perceived by the students as something to be memorised and learned by rote. This method only serves to re-emphasise that mathematics is about learning facts and procedures by heart, while the purpose of the concept of proof is often not made clear.
In this unit you will think about mathematical proof and how it can be used to develop deeper mathematical understanding with your students. You will learn how to help your students become more verbally fluent in their reasoning and how they can learn effectively from discussions.
What you can learn in this unit
- How to enable students to describe and articulate their mathematical thinking processes.
- How to facilitate students learning through talking.
- Some suggestions to address differential levels of attainment in teaching proofing.
This unit links to the teaching requirements of the NCF (2005) and NCFTE (2009) outlined in Resource 1.
1 Why teach mathematical proof in schools?
There are many discussions around the world about whether mathematical proof should be part of the school curriculum. Teachers often struggle with teaching proof and students often struggle with learning it. It is also not always clear what mathematical learning is addressed by working on proof. Some countries have abandoned teaching mathematical proof altogether, although others approach it more as reasoning in mathematics. In India, mathematical proof is still prevalent in the school curriculum and a number of chapters in textbooks for Class IX and X include mathematical proofs.
There are many positives for learning mathematical thinking to be gained from working on mathematical proof in schools. Researchers suggest working on mathematical proof offers a variety of mathematical learning opportunities. Hanna (2000) summarised these as:
- verification of the truth of a statement
- explanation by providing insight into why it is true
- systematisation by organising various results into a deductive system of axioms, major concepts and theorems
- discovery or invention of new results
- communication in order to transmit mathematical knowledge
- construction of an empirical theory
- exploration of the meaning of a definition or the consequences of an assumption
- incorporation of a well-known fact into a new framework and thus viewing it from a fresh perspective.
This unit will explore and give suggestions on how the process of mathematical proving can be used as a tool for developing students’ understanding of mathematics by working on learning opportunities like those above.
Pause for thought What are your thoughts and opinions about mathematical proof in the school curriculum? Should it be there? Do you agree with the list of learning opportunities suggested by these researchers? Which ones do you consider to be most important? Does this kind of mathematical learning currently happen in your classroom? If so, how do you make it happen? If not, do you have any ideas about what you would like to change in your current practice? |
2 Is it proof?
Mathematical proof is different from proof in other subjects such as science and law because every step in the argumentation has to be based on known and undisputed facts – proof cannot be based on empirical evidence. This means that in mathematics, you cannot state ‘this is always true’ from simply observing occurrences. In mathematics, alljustification of proof should be based on accepted or established statements, and rules of logic.
To learn, and to make sense of new learning, students need to be able to build on their existing knowledge and experiences, something that is hard to do when moving straight into formal mathematical proof. The remainder of this unit will suggest ways to offer students support in identifying and developing the important aspects in mathematical proving, including:
- the argument that mathematical proofs are not built on empirical evidence
- knowing and recall of mathematical properties
- developing effective argumentation techniques
- building on what is already known.
Sometimes it is hard to know when mathematical reasoning can be considered a ‘proof’ or not. An example of this is described in the following scenario, in which Mrs Kapur asked his students how they would prove that the sum of angles of a triangle is equal to 180°.
Case Study 1: Mrs Kapur asks her class to prove that the sum of the angles of a triangle equals 180°
| Teacher: | What do the interior angles of a triangle add up to? |
| Student: | 180°. |
| Teacher: | Are you sure? |
| Student: | Yes, absolutely. |
| Teacher: | How do you know this is so? |
| Student: | Because … you tell us and it says so in the book. |
| Teacher: | OK, I want you to now think carefully for a moment about how you would prove mathematically that the sum of the angles of a triangle equals 180°. This is a mathematical proof, so your reasoning has to be rigorous and convincing. Imagine you are a mathematician trying to convince the prime minister of India – how would you go about it? Think about what you know already about triangles and mathematical proof. Discuss your ideas first with your partner. I will give you five minutes to do so. |
| [Five minutes later.] | |
| So, what will you say to the prime minister to convince him that the sum of the interior angles of a triangle always equals 180°? | |
| Student 1: | We would say that when you measure the interior angles of a triangle and add these up, then you always end up with 180°. You can do this with any number, and any kind of triangle. |
| Student 2: | We would say: draw a triangle on a piece of paper. Cut it out. Tear off the corner and place these corners next to each other. They always fit on a straight line. As we know that angles on a straight line add up to 180°, we can deduce that the sum of the interior angles of a triangle also equals 180°. This will always be so for any triangle. |
| Teacher: | What do you think, class – are you convinced these ideas are mathematical proofs? Will the prime minister be convinced? Should he be? |
Pause for thought Think about how far these ideas are indeed mathematical proofs. Are there other ways that proof might be offered? How might these proofs be challenged? |
3 Coming to know mathematical properties and facts
The students of Mrs Kapur’s class came up with examples of how they could go about creating a mathematical proof. However, neither can be considered a mathematical proof because the arguments used are not all based on accepted or established statements. Although the second suggestion uses the fact that angles on a line add up to 180°, it is not ‘proof’ that the three angles would always ‘fit’. The students might argue that it just ‘works’, but such a justification is based on empirical evidence and not on the mathematical properties of angles in a triangle.
Proving theorems should be done by building on existing theorems and axioms; however, you have to know some of these first before you can start building on them! Yet once you know some, you can deduce many others from these and develop your own corollaries.
Activity 1 lists some established and accepted statements that are useful in school mathematics. Some are from classical geometry and useful in the above proof, but the examples also make clear that theorems appear in more areas of mathematics than just geometry. The task is for your students to add some more to the list, and to use their imagination and natural deduction skills write down some statements of their own that follow on from the given statements. A good phrase to use to trigger such thinking is: ‘When I know something, then I also know something else.’ By doing this, students will also make connections between different concepts and start practising their skills of deduction.
Before attempting to use the activities in this unit with your students, it would be a good idea to complete all (or at least part) of the activities yourself. It would be even better if you could try them out with a colleague, as that will help you when you reflect on the experience. Trying the activities yourself will mean that you get insights into learners’ experiences that can in turn influence your teaching and your experiences as a teacher. When you are ready, use the activities with your students. After the lesson, think about how that the activity went and the learning that took place. This will help you to develop a more learner-focused teaching environment.
Activity 1: Making a useful list of established and accepted facts
Tell your students that Table 1 lists some established and accepted statements that are useful in school mathematics. Note that the first four rows are from the five ‘common notions’ that Euclid, the famous Ancient Greek mathematician known as ‘the father of geometry’, wrote in his book Elements.
| Established or accepted statement or fact | Write or draw an example | When I know this then I also know that … |
|---|---|---|
| Things that are equal to the same thing are also equal to one another (transitive property of equality) | ||
| If equals are added to equals, then the results are equal | 7 + 3 = 4 + 6 23 – 4 = 19 – 0 Hence: 7 + 3 + 23 – 4 = 4 + 6 + 19 - 0 | |
| If equals are subtracted from equals, then the remainders are equal | ||
| The whole is greater than any of its parts | ||
| Angles at a point add up to 360° | 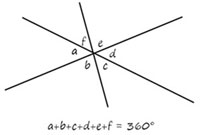 | The angle of a straight line is 180° |
| When a line intersects (or crosses) a set of parallel lines, then vertically opposite angles are equal and corresponding angles are equal |  | Alternate angles are equal |
| If two lines intersect each other, the vertically opposite angles are equal | ||
Ask your students the following questions:
- Do you recognise any of these? Can you add a drawing of what they might mean?
- Do you know any other established and accepted statements that you could add to this list?
- Look at the statements again and think: ‘When I know this, then I also know that …’. Write these down. You are now inventing your own mathematical statements!
- Discuss your work and your thinking with your partner, and try to convince them that you are right!
Activity 2: Proving that the sum of the angles of a triangle equals 180°
Tell your students that using the facts about angles of a line intersecting parallel lines can prove that the sum of the angles of a triangle equals 180°.
(It might help to read Case Study 1 to your students for this activity.)
Now tell your students:
- Have a go at putting such a proof together. Use the phrase ‘When I know this then I also know that …’ to help you in your reasoning.
- Discuss your work and your thinking with a partner, and try to convince them that you are right!
Case Study 2: Mrs Agarwal reflects on using Activities 1 and 2
This is the account of a teacher who tried Activities 1 and 2 with her secondary students.
Because they had some examples to work from, students were happy to draw what the statements could mean. They did find Euclid’s common notions somewhat difficult to understand and it led to an interesting discussion that the mathematical language they are exposed to is not that unclear in comparison!
Ranu asked whether something like ‘ A = 30° and A= B so B = 30°’ was allowed for the statement ‘Things that are equal to the same thing are also equal to one another.’ I did not confirm or deny this, because I wanted Ranu to decide whether it was a good idea. I replied by reiterating what it said in the task:
- ‘When you know this, then you also know what?’
- ‘Try and convince your partner that you are right.’
For Activity 2 I used the approach suggested. First I read the case study about Mrs Kapur’s class aloud to them; then I asked the questions from the reflection point: ‘What do you think, class – are you convinced these ideas are mathematical proofs? Will the prime minister be convinced? Should he be convinced?’ My reasons for doing so were that I thought if I asked them to prove that the sum of the angles of a triangle equals 180°, they would come up with similar proofs as the students in Mrs Kapur’s class and I wanted to start the activity with knowing this would not be considered a proof. Most students initially agreed that what Mrs Kapur’s students had come up with was a convincing proof, but a few students were not sure. I asked them why; they said they were not convinced these proofs were built on established or accepted facts. This led to a discussion about empirical evidence, what it was and why it is not allowed in mathematical proof.
Only then did I introduce Activity 2 and ask the students to play with it, try things out and experiment. This seemed to relax them and they happily worked on it, discussing their thoughts and trying out their arguments with their neighbours. Later on, we discussed their ideas with the whole class. Some proofs did not convince the rest of the class, but several students had developed solid justification for their proof.
I also found some online videos that show the proof, such as one created by the Khan Academy [see ‘Additional resources’, below]. Although I could not show it in the classroom, I did mention it to the students to make them aware of its existence.
Reflecting on your teaching practice
When you do such an exercise with your class, reflect afterwards on what went well and what went less well. Consider the questions that made the students interested and able to work, and those where you needed to clarify. Such reflection always helps with finding a ‘script’ which helps you engage the students to find mathematics interesting and enjoyable. If they do not understand and cannot do something, they are less likely to become involved. Use this reflective exercise every time you undertake the activities, noting, as Mrs Agarwal did, some quite small things that made a difference.
Pause for thought Good questions to trigger reflection are:
|
4 Task design to help students think about mathematical properties
In Activity 2, students constructed their own mathematical ‘truths’ by building on their natural powers for deductive reasoning and using their knowledge of mathematical properties. Knowing about mathematical properties is very important, because any argumentation in mathematical proof should be based on these. Similarly, defining mathematical conditions about when a statement applies and when it does not is equally important.
Sorting and classifying tasks are effective in supporting students to become aware of defining properties and conditions for mathematical sets; that is, which properties belong to which set. Sorting and classifying makes you think about differences and similarities. The next activity uses this approach.
Activity 3: Sorting and classifying to find properties and conditions
Tell your students that a ‘proportion’ is a pair of ratios that are equal. Being proportional is a property that occurs frequently in mathematics across different topics and concepts.
The statements that follow describe some scenarios that illustrate mathematical concepts. Ask your students to read these and classify whether they would be proportional or not, and under what conditions. They should provide their reasons and explain to a friend what the example would be proportional (or not proportional) to. Be critical!
- a.Enlarging a photograph.
- b.Cutting slices of bread to make a sandwich.
- c.The equation of a linear equation in one variable (ax + b = 0).
- d.The work done by some number of people in a given time frame.
- e.The amount of money spent by a number of people to watch a particular movie at a particular cinema.
- f.The fare for tickets for train journeys.
- g.Dividing a line segment into m equal parts.
- h.The height of Qutab Minar (Figure 1).
Figure 1 Qutab Minar, Delhi.
- i.The area of a circle.
- j.The area of a square.
- k.The product of the height of a cylinder and its radius.
- l.The volume of a cone.
- m.A rickshaw fare.
Case Study 3: Mrs Agarwal reflects on using Activity 3
To help the students engage with this activity, we read the instructions and examples (a) and (b) together aloud in the classroom. We then had a brainstorm about possible answers for (a), and discussed the conditions that would need to be fulfilled for the enlarged photograph to stay proportional to the old one. This was started by Rahul, who said that to enlarge the photograph to make it twice as big, you would have to double its width. I could see that Usha was thinking, as she was frowning, and then she said that would not work because it would make the picture look weird.
I then asked the students to first work on the examples individually so they could develop their own thoughts and ideas first, and then to discuss their thinking and reasoning with their partner.
After some time, I picked some statements to discuss with the whole class and for the students to share their ideas. I noticed that students were using some phrases repetitively, such as:
- ‘But what if …?’
- ‘If you change this, then that changes/still stays the same.’
- ‘This is the same, this is different.’
I pointed this out to the students and they agreed that these were good phrases to find out about mathematical properties and conditions. Two students quickly wrote the phrases and a title ‘Good phrases to find out about mathematical properties and conditions’ on a large piece of paper, which was then stuck on the wall.
Pause for thought
|
5 Learning to convince
The formal rules of argumentation and deduction that are used in mathematical proof are not easy to teach at school level. The language used is alien and the concepts are often considered to be far removed from the world of the students’ experience. To some extent this is surprising, because reasoning and deduction are skills and powers that we all have, along with knowing about different levels of convincing, which is the same as rigour.
The next two activities aim to use the skills and experiences that students have from everyday reasoning to make their reasoning more structured and formal. In this way it builds on what students know and do already. The first one uses the task design of ‘always true, sometimes true or never true’ to find out whether and when a statement is valid.
The results of this activity are then used in the next one, where students work on different levels of rigour in their reasoning and argumentation. The task design here uses the approach of ‘convince yourself, convince a friend, convince Ramanujan’.
Distinguishing who needs to be convinced helps students to become more precise. Convincing yourself is often easy: you may be happy with empirical evidence and the language used can be sloppy and vague, as there is no need to explain it aloud. Convincing a friend requires more precision in the use of language, as the thoughts need to be organised and verbalised for communication and the validity of the arguments used. However, your friend might still be willing to accept what you are saying because they are your friend, although they might challenge you more than you would challenge yourself. To convince Ramanujan, the great Indian mathematician, requires students to come up with solid mathematical justification, because he will try and pick holes in their reasoning. To convince Ramanujan, argumentation will have to be based on accepted or established mathematical statements because only those are indisputable.
Activity 4: Always, sometimes or never true
Preparation
The statements underneath require the students to have some knowledge about these topics. Choose the ones that are relevant to your classroom.
The activity
Tell your students the following:
- Read the following statements. Which of these are always true, sometimes true or never true? Discuss your reasoning with your partner.
- a.If p is a prime number, then p + 1 is a composite number.
- b.N chords of a circle divide the circular region into N + 1 non-overlapping regions.
- c.If the volumes of two spheres are equal, then the spheres are congruent.
- d.The centroid of a triangle lies inside the triangle.
- e.There are infinitely many prime numbers.
- Make up some more statements of your own and give them to your partner. Which of these are always true, sometimes true or never true?
Activity 5: Convince yourself, convince a friend, convince Ramanujan
Tell your students:
- Remember that Ramanujan will try and pick holes in your reasoning.
- Redo Activity 4, but instead of simply discussing your reasoning with your partner, you now have to come up with justification that will:
- convince yourself
- convince a friend
- convince Ramanujan.
- Share your most convincing justification with the class. Are the other students convinced by your argumentation?
Case Study 4:Mrs Nagaraju reflects on using Activities 4 and 5
I decided to do Activity 4 – discussion whether a statement is always, sometimes or never true – by putting students in groups of three and four, because I thought this would give them the opportunity to generate more ideas. I did notice that, in this case, the groups of three seemed to work better – they were more engaged with each other – while in a number of the groups of four there were students not engaging and only listening. For Activity 5, I asked them to work in pairs to give everyone a chance and the time to practise their justification. A good thing about these tasks is that it forces students to have an opinion and to make them come up with justification even if they only had been listening previously.
When I asked the students whether there had been a difference in their argumentation to convince oneself, a friend or Ramanujan, they said that indeed in some cases it made them become more precise and thorough. However, in other cases some students felt they could not come up with reasons in their argumentation because they could not think of any – they just knew the statement was correct because they had learnt it from me! To help them think about steps that might help them to develop a logical argument I thought that someone in the classroom would have some suggestion and maybe they would be more critical when it came from another student instead of me. I asked the groups to point out which statements this had happened with and asked other students if they had come up with some justification. The justification was explained to the whole class and I asked the all the students to be critical of the justifications just as real mathematicians would be. After this I went back to those students who had been stuck and they said that the discussion had helped them to get unstuck.
For more ideas about using questioning and talk for learning in your classroom, see Resources 2 and 3.
Pause for thought
|
6 Summary
Mathematics learning, especially about proof, is often seen by students to be wholly about learning and memorising facts and procedures. Developing mathematical reasoning with students not only allows them to construct mathematical ‘truths’ for themselves but also helps them to understand mathematics. Reasoning mathematically requires them to explore and use mathematical properties to make their arguments. Constructing mathematical reasoning in this way is often considered to be the beauty of the subject, and is certainly one of the core concepts of the subject. By working with your students on proof you are inviting them to act as mathematicians and to appreciate some of the fascination of mathematics.
Pause for thought Identify three ideas that you have used in this unit that would work when teaching other topics. Make a note of two topics you have to teach soon where those ideas can be used, perhaps with some small adjustments. |
Resources
Resource 1: NCF/NCFTE teaching requirements
This unit links to the following teaching requirements of the NCF (2005) and NCFTE (2009), and will help you to meet those requirements:
- View learners as active participants in their own learning and not as mere recipients of knowledge; to encourage their capacity to construct knowledge; to ensure that learning shifts away from rote methods.
- View learning as a search for meaning out of personal experiences and knowledge generation as a continuously evolving process of reflective learning.
- Help students to see mathematics as something to talk about, to communicate through, to discuss among themselves, to work together on.
Resource 2: Using questioning to promote thinking
Teachers question their students all the time; questions mean that teachers can help their students to learn, and learn more. On average, a teacher spends one-third of their time questioning students in one study (Hastings, 2003). Of the questions posed, 60 per cent recalled facts and 20 per cent were procedural (Hattie, 2012), with most answers being either right or wrong. But does simply asking questions that are either right or wrong promote learning?
There are many different types of questions that students can be asked. The responses and outcomes that the teacher wants dictates the type of question that the teacher should utilise. Teachers generally ask students questions in order to:
- guide students toward understanding when a new topic or material is introduced
- push students to do a greater share of their thinking
- remediate an error
- stretch students
- check for understanding.
Questioning is generally used to find out what students know, so it is important in assessing their progress. Questions can also be used to inspire, extend students’ thinking skills and develop enquiring minds. They can be divided into two broad categories:
- Lower-order questions, which involve the recall of facts and knowledge previously taught, often involving closed questions (a yes or no answer).
- Higher-order questions, which require more thinking. They may ask the students to put together information previously learnt to form an answer or to support an argument in a logical manner. Higher-order questions are often more open-ended.
Open-ended questions encourage students to think beyond textbook-based, literal answers, thus eliciting a range of responses. They also help the teacher to assess the students’ understanding of content.
Encouraging students to respond
Many teachers allow less than one second before requiring a response to a question and therefore often answer the question themselves or rephrase the question (Hastings, 2003). The students only have time to react – they do not have time to think! If you wait for a few seconds before expecting answers, the students will have time to think. This has a positive effect on students’ achievement. By waiting after posing a question, there is an increase in:
- the length of students’ responses
- the number of students offering responses
- the frequency of students’ questions
- the number of responses from less capable students
- positive interactions between students.
Your response matters
The more positively you receive all answers that are given, the more students will continue to think and try. There are many ways to ensure that wrong answers and misconceptions are corrected, and if one student has the wrong idea, you can be sure that many more have as well. You could try the following:
- Pick out the parts of the answers that are correct and ask the student in a supportive way to think a bit more about their answer. This encourages more active participation and helps your students to learn from their mistakes. The following comment shows how you might respond to an incorrect answer in a supportive way: ‘You were right about evaporation forming clouds, but I think we need to explore a bit more about what you said about rain. Can anyone else offer some ideas?’
- Write on the blackboard all the answers that the students give, and then ask the students to think about them all. What answers do they think are right? What might have led to another answer being given? This gives you an opportunity to understand the way that your students are thinking and also gives your students an unthreatening way to correct any misconceptions that they may have.
Value all responses by listening carefully and asking the student to explain further. If you ask for further explanation for all answers, right or wrong, students will often correct any mistakes for themselves, you will develop a thinking classroom and you will really know what learning your students have done and how to proceed. If wrong answers result in humiliation or punishment, then your students will stop trying for fear of further embarrassment or ridicule.
Improving the quality of responses
It is important that you try to adopt a sequence of questioning that doesn’t end with the right answer. Right answers should be rewarded with follow-up questions that extend the knowledge and provide students with an opportunity to engage with the teacher. You can do this by asking for:
- a how or a why
- another way to answer
- a better word
- evidence to substantiate an answer
- integration of a related skill
- application of the same skill or logic in a new setting.
Helping students to think more deeply about (and therefore improve the quality of) their answer is a crucial part of your role. The following skills will help students achieve more:
- Prompting requires appropriate hints to be given – ones that help students develop and improve their answers. You might first choose to say what is right in the answer and then offer information, further questions and other clues. (‘So what would happen if you added a weight to the end of your paper aeroplane?’)
- Probing is about trying to find out more, helping students to clarify what they are trying to say to improve a disorganised answer or one that is partly right. (‘So what more can you tell me about how this fits together?’)
- Refocusing is about building on correct answers to link students’ knowledge to the knowledge that they have previously learnt. This broadens their understanding. (‘What you have said is correct, but how does it link with what we were looking at last week in our local environment topic?’)
- Sequencing questions means asking questions in an order designed to extend thinking. Questions should lead students to summarise, compare, explain or analyse. Prepare questions that stretch students, but do not challenge them so far that they lose the meaning of the questions. (‘Explain how you overcame your earlier problem. What difference did that make? What do you think you need to tackle next?’)
- Listening enables you to not just look for the answer you are expecting, but to alert you to unusual or innovative answers that you may not have expected. It also shows that you value the students’ thinking and therefore they are more likely to give thoughtful responses. Such answers could highlight misconceptions that need correcting, or they may show a new approach that you had not considered. (‘I hadn’t thought of that. Tell me more about why you think that way.’)
As a teacher, you need to ask questions that inspire and challenge if you are to generate interesting and inventive answers from your students. You need to give them time to think and you will be amazed how much your students know and how well you can help them progress their learning.
Remember, questioning is not about what the teacher knows, but about what the students know. It is important to remember that you should never answer your own questions! After all, if the students know you will give them the answers after a few seconds of silence, what is their incentive to answer?
Resource 3: Talk for learning
Why talk for learning is important
Talk is a part of human development that helps us to think, learn and make sense of the world. People use language as a tool for developing reasoning, knowledge and understanding. Therefore, encouraging students to talk as part of their learning experiences will mean that their educational progress is enhanced. Talking about the ideas being learnt means that:
- those ideas are explored
- reasoning is developed and organised
- as such, students learn more.
In a classroom there are different ways to use student talk, ranging from rote repetition to higher-order discussions.
Traditionally, teacher talk was dominant and was more valued than students’ talk or knowledge. However, using talk for learning involves planning lessons so that students can talk more and learn more in a way that makes connections with their prior experience. It is much more than a question and answer session between the teacher and their students, in that the students’ own language, ideas, reasoning and interests are given more time. Most of us want to talk to someone about a difficult issue or in order to find out something, and teachers can build on this instinct with well-planned activities.
Planning talk for learning activities in the classroom
Planning talking activities is not just for literacy and vocabulary lessons; it is also part of planning mathematics and science work and other topics. It can be planned into whole class, pair or groupwork, outdoor activities, role play-based activities, writing, reading, practical investigations, and creative work.
Even young students with limited literacy and numeracy skills can demonstrate higher-order thinking skills if the task is designed to build on their prior experience and is enjoyable. For example, students can make predictions about a story, an animal or a shape from photos, drawings or real objects. Students can list suggestions and possible solutions about problems to a puppet or character in a role play.
Plan the lesson around what you want the students to learn and think about, as well as what type of talk you want students to develop. Some types of talk are exploratory, for example: ‘What could happen next?’, ‘Have we seen this before?’, ‘What could this be?’ or ‘Why do you think that is?’ Other types of talk are more analytical, for example weighing up ideas, evidence or suggestions.
Try to make it interesting, enjoyable and possible for all students to participate in dialogue. Students need to be comfortable and feel safe in expressing views and exploring ideas without fear of ridicule or being made to feel they are getting it wrong.
Building on students’ talk
Talk for learning gives teachers opportunities to:
- listen to what students say
- appreciate and build on students’ ideas
- encourage the students to take it further.
Not all responses have to be written or formally assessed, because developing ideas through talk is a valuable part of learning. You should use their experiences and ideas as much as possible to make their learning feel relevant. The best student talk is exploratory, which means that the students explore and challenge one another’s ideas so that they can become confident about their responses. Groups talking together should be encouraged not to just accept an answer, whoever gives it. You can model challenging thinking in a whole class setting through your use of probing questions like ‘Why?’, ‘How did you decide that?’ or ‘Can you see any problems with that solution?’ You can walk around the classroom listening to groups of students and extending their thinking by asking such questions.
Your students will be encouraged if their talk, ideas and experiences are valued and appreciated. Praise your students for their behaviour when talking, listening carefully, questioning one another, and learning not to interrupt. Be aware of members of the class who are marginalised and think about how you can ensure that they are included. It may take some time to establish ways of working that allow all students to participate fully.
Encourage students to ask questions themselves
Develop a climate in your classroom where good challenging questions are asked and where students’ ideas are respected and praised. Students will not ask questions if they are afraid of how they will be received or if they think their ideas are not valued. Inviting students to ask the questions encourages them to show curiosity, asks them to think in a different way about their learning and helps you to understand their point of view.
You could plan some regular group or pair work, or perhaps a ‘student question time’ so that students can raise queries or ask for clarification. You could:
- entitle a section of your lesson ‘Hands up if you have a question’
- put a student in the hot-seat and encourage the other students to question that student as if they were a character, e.g. Pythagoras or Mirabai
- play a ‘Tell Me More’ game in pairs or small groups
- give students a question grid with who/what/where/when/why questions to practise basic enquiry
- give the students some data (such as the data available from the World Data Bank, e.g. the percentage of children in full-time education or exclusive breastfeeding rates for different countries), and ask them to think of questions you could ask about this data
- design a question wall listing the students’ questions of the week.
You may be pleasantly surprised at the level of interest and thinking that you see when students are freer to ask and answer questions that come from them. As students learn how to communicate more clearly and accurately, they not only increase their oral and written vocabulary, but they also develop new knowledge and skills.
Additional resources
- ‘Proof – sum of measures of angles in a triangle are 180’ by Khan Academy: https://www.khanacademy.org/ math/ geometry/ angles/ v/ proof---sum-of-measures-of-angles-in-a-triangle-are-180
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
Except for third party materials and otherwise stated below, this content is made available under a Creative Commons Attribution-ShareAlike licence (http://creativecommons.org/ licenses/ by-sa/ 3.0/). The material acknowledged below is Proprietary and used under licence for this project, and not subject to the Creative Commons Licence. This means that this material may only be used unadapted within the TESS-India project and not in any subsequent OER versions. This includes the use of the TESS-India, OU and UKAID logos.
Grateful acknowledgement is made to the following sources for permission to reproduce the material in this unit:
Figure 1: Clare Lee for The Open University.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked the publishers will be pleased to make the necessary arrangements at the first opportunity.
Video (including video stills): thanks are extended to the teacher educators, headteachers, teachers and students across India who worked with The Open University in the productions.
