धनात्मक और ऋणात्मक संख्याओं को पढ़ाने के लिए संख्या रेखा और 'कल्पना करना यदि' ...की अभिव्यक्ति का उपयोग करना।

यह इकाई किस बारे में है

इस इकाई में आप वे उपाय देखेंगे जिनके तहत आप विद्यार्थियों को संख्याओं का अर्थ और यह जानने के लिए प्रोत्साहित कर सकते हैं कि ‘ऋणात्मक संख्याओं’ की अवधारणा क्यों विकसित की गई थी।

विद्यार्थी सबसे पहले ऋण चिह्न को तब देखते हैं जब उसका उपयोग अंकों को घटाने के लिए किया जाता है; इसलिए, ऋणात्मक संख्याओं में उसके उपयोग का ध्यान पूर्वक परिचय कराना होगा। यह समझाने से कि यह चिह्न अलग तरीके से इस्तेमाल किया जाता है और यह पता लगाने से कि ऋणात्मक संख्याओं के लिए इसका उपयोग क्यों किया जाता है, आपके विद्यार्थियों को इस चिह्न के उपयोग की समानताएं और अंतरों को समझने और पहचानने में मदद मिलेगी।

इस इकाई की गतिविधियों के माध्यम से आप एक संख्या रेखा के उपयोग को विकसित करने के बारे में भी सोचेंगे ताकि आपके विद्यार्थी धनात्मक और ऋणात्मक अंकों के द्वारा दर्शाए गए परिवर्तनों को समझ सकें। दरअसल उन परिवर्तनों को खुद करने से विद्यार्थियों को यह भी समझने में आगे मदद मिलेगी कि ‘धनात्मक’ और ‘ऋणात्मक’ का अर्थ क्या होता है। गणित पढ़ाते समय कल्पना को पंख देने के लिए ‘कल्पना करें यदि …’ कहने का महत्व भी समझाया गया है।

आप इस इकाई में क्या सीख सकते हैं

• धनात्मक और ऋणात्मक संख्याओं के बीच अंतर को समझने में आपके विद्यार्थियों की मदद करने के लिए कुछ विचार।
• गणित सीखने के लिए आपके विद्यार्थियों की कल्पना को प्रोत्साहित करने के लिए ‘कल्पना करें यदि …’ कथन की भूमिका।

• धनात्मक और ऋणात्मक संख्याओं को समझने के लिए संख्या रेखा का उपयोग कैसे करें।

इस इकाई का संबंध NCF (2005) और NCFTE (2009) की दर्शाई गई शिक्षण आवश्यकताओं से है। संसाधन 1

1 संख्याओं का अर्थ

संख्याओं का आविष्कार संभवतः जानवरों या अन्य वस्तुओं को गिनने के उद्देश्य से किया गया था। संख्या प्रणाली में मूल रूप से केवल ‘एक’, ‘दो’ और ‘कई’ के लिए शब्द होते थे क्योंकि बस इसी की ज़रूरत होती थी। आगे विकास होने पर मवेशियों को गिनने की ज़रूरत पड़ी, और आज की प्रचलित संख्या प्रणाली विकसित की गई, जिसमें शून्य और ऋणात्मक संख्याएं शामिल हैं। संख्याओं के नाम लगभग हमेशा एक तार्किक प्रणाली का उपयोग करके निर्मित किए जाते हैं ताकि वे ऐसी संख्याओं को व्यक्त कर सकें जो सभी आशयों और उद्देश्यों के लिए, अनंत हों।

संख्याएं निम्नलिखित का प्रतिनिधित्व करने के लिए उपयोग की जाती हैं:

• मात्रा या परिमाण, जैसे ‘कितने?’ या ‘कितनी दूर?’ आदि प्रश्नों का उत्तर देने के लिए
• संख्याओं के बीच संबंध दर्शाने के लिए, ‘और कितने अधिक?’ या, ‘और कितने कम?’ जैसे प्रश्नों का उत्तर देने के लिए
• मात्रा या परिमाण के संदर्भ में रूपांतरण, ‘मान लीजिए ज़ूरी पर मैरी के तीन रुपए उधार हैं। उसमें से उसने मैरी को एक रुपया दे दिया। तो अब उसका कितना उधार बाकी है?’, या ‘मनु ने पहले मैच में तीन गोटियां जीतीं और दूसरे मैच में पांच गोटियां हारीं। उसने कुल कितनी गोटियां हारीं?’ जैसे प्रश्नों का उत्तर देने के लिए

विचार के लिए रुकें विचार करें कि ऋणात्मक नंबर आपके विद्यार्थियों के समक्ष कैसे और कहां आए होंगे। उदाहरण के लिए, उनके मन में यह विचार आया होगा कि आइसक्रीम फ़्रीज़र में तापमान शून्य से कम होता है। ऐसे विचार उनके समक्ष और कहां आए होंगे?

शून्य एक संख्या है

संख्याओं को समझने में शून्य एक महत्वपूर्ण भूमिका निभाता है। गणितीय रूप से, शून्य को कई उपयोग और अर्थ दिए गए हैं जिनके साथ विद्यार्थियों को कार्य करना पड़ता है। एक अर्थ में, मात्रा ‘कुछ नहीं’ दर्शाई जाती है। इसका अर्थ ‘कोई नहीं’ हो सकता है, जैसे ‘एक फ़ुटबॉल मैच में एक टीम ने कोई गोल नहीं किया’, या इसका मतलब किसी संख्या जैसे 600 में ‘कोई इकाई या दहाई नहीं’ हो सकता है।

शून्य का उपयोग एक एकपक्षीय संदर्भ बिंदु या मूल के एक निर्देशांक के रूप में भी किया जाता है, उदाहरण के लिए (0, 0)। इस बिंदु से कम से कम दो परस्पर विपरीत दिशाओं पर विचार किया जा सकता है। ऋणात्मक संख्याएं सिखाते समय यह समझना महत्वपूर्ण है कि शून्य के ये सारे अलग अलग अर्थ हैं।

ऋणात्मक संख्याएं

जब किसी संख्या के आगे एक ऋणात्मक या ऋण चिह्न लगाया जाता है, तो वह शून्य के सापेक्ष उस संख्या की ऋणात्मकता दर्शाता है। प्राकृतिक संख्याओं को धनात्मक संख्या माना जाता है।

धनात्मक और ऋणात्मक दोनों संख्याओं के परिमाण और दिशा दोनों होते हैं। ऋणात्मक संख्याएं परिमाण और क्रम के बीच ग़लतफहमी उत्पन्न कर सकती हैं। उदाहरण के लिए, –4 पारंपरिक रूप से –1 से कम होता है, इसके बावजूद कि –4 का परिमाण –1 से अधिक दिखाई देता है।

विचार के लिए रुकें उस समय की सोचें जब आप ऋणात्मक संख्याएं सीख रहे थे। क्या वह उस समय एकदम सीधा प्रतीत हुआ था? यह बताने का प्रयास करें कि ऋणात्मक संख्याएं आपको सीधी क्यों प्रतीत हुईं (यदि हुईं तो)। क्या शायद ऐसा इसलिए था क्योंकि ऋणात्मक संख्याएं प्राकृतिक संख्याओं के बारे में आपके विचार के साथ एकदम उपयुक्त थीं और उसने उस सोच को संतोषजनक रूप से आगे बढ़ाया? यह याद करने का प्रयास करें कि आप ऋणात्मक संख्याओं पर गणितीय विधियों को करना कैसे समझ सके - क्या आपने पहले उन नियमों को याद कर लिया था? अपनी कक्षा के कुछ विद्यार्थियों के बारे में सोचें और प्राकृतिक संख्याओं के साथ उन्हें आने वाली समस्याओं के बारे में सोचें। उन विद्यार्थियों के बारे में सोचें जिन्हें आपने पढ़ाया है, कि कैसे वो ‘दो ऋण मिल कर एक धन बनाते हैं’ नियम को लागू करने के बारे में दुविधा में पड़ सकते हैं। कैसे आपके विद्यार्थियों को केवल नियमों को याद करने पर निर्भर रहने के बजाय उन्हें ऋणात्मक संख्याओं को समझने में मदद की जा सकती है?

2 ऋणात्मक संख्याओं की आवश्यकता

इस इकाई की गतिविधियों के माध्यम से आप इस बारे में अपने विद्यार्थियों की समझ को विकसित कर सकेंगे कि ऋणात्मक संख्याओं का उपयोग क्यों किया जाता है और ये कितनी उपयोगी हो सकती हैं। इसमें आपको युक्तियां भी बताई जाएंगी कि आपके विद्यार्थियों को यह समझने में कैसे मदद की जाए कि केवल नियमों को याद करने के बजाय ऋणात्मक संख्याओं के साथ कैसे काम किया जाए। पहली गतिविधि इस तरह डिज़ाइन की गई है कि विद्यार्थियों को संख्या प्रणाली के एक हिस्से के रूप में ऋणात्मक संख्याओं की ज़रूरत को समझने में मदद मिले।

इस अंक में अपने विद्यार्थियों के साथ गतिविधियों के उपयोग का प्रयास करने से पहले अच्छा होगा कि आप सभी गतिविधियों को पूरी तरह या आंशिक रूप से स्वयं करके देखें। यह और भी बेहतर होगा यदि आप इसका प्रयास अपने किसी सहकर्मी के साथ करें क्योंकि जब आप अनुभव पर विचार करेंगे तो आपको मदद मिलेगी। स्वयं प्रयास करने से आपको शिक्षार्थी के अनुभवों के भीतर झांकने का मौका मिलेगा जिसके फलस्वरूप यह आपके शिक्षण और एक शिक्षक के रूप में आपके अनुभवों को प्रभावित करेगा।

वीडियो: स्थानीय संसाधनों का उपयोग करते हुए

आपके शिक्षण अभ्यास के बारे में सोचना

अपनी कक्षा के साथ ऐसा कोई अभ्यास करने पर बाद में यह सोचें कि क्या ठीक रहा और कहाँ गड़बड़ी हुई। ऐसे प्रश्न सोचें जिनसे विद्यार्थियों में रुचि पैदा हो तथा उनके बारे में उन्हें समझाएँ ताकि वे उन्हें हल करके आगे बढ़ सकें। ऐसे चिंतन से वह ‘समझ’ मिल जाती है, जिसकी मदद से आप विद्यार्थियों के मन में गणित के प्रति रुचि जगा सकते हैं और उसे मनोरंजक बना सकते हैं। जब आप सोचते हैं कि गतिविधि 1 के उपाय आपकी कक्षा के साथ कैसे रहे, तो श्रीमती कपूर की तरह छोटी छोटी खास बातों का एक नोट बना लें।

विचार के लिए रुकें केस स्टडी में, श्रीमती कपूर ने कहा कि वह उनमें से कुछ गतिविधियां दोहरा कर उनके परिणामों को गणितीय अंकनों और सवालों की मदद से ब्लैकबोर्ड पर दर्ज करने के बारे में सोच रही थीं। विद्यार्थियों द्वारा गतिविधियों और गेम्स का बहुत अधिक अनुभव लेने के बाद आपके विचार से ऐसा करने के क्या फ़ायदे हो सकते हैं? अब निम्नलिखित प्रश्नों के बारे में सोचें: आपकी कक्षा में गतिविधियां और गेम कैसे रहे? विद्यार्थियों से किस प्रकार की प्रतिक्रिया अनपेक्षित थी? इससे धनात्मक और ऋणात्मक संख्याओं की उनकी समझ के बारे में आपको क्या पता चलता है? अपने विद्यार्थियों की समझ का पता लगाने के लिए आपने क्या सवाल किए? किन बिंदुओं पर आपको लगा कि आपको और समझाना होगा? अपने शिक्षण में अगली बार इन गतिविधियों को उपयोग करने पर आप क्या अलग करेंगे?

3 धनात्मक और ऋणात्मक संख्याओं की समझ विकसित करने के लिए संख्या रेखाओं का उपयोग करना

संख्या रेखा, जैसे कि चित्र 1 में दी गई है, एक ज्यामितीय विचार है जिसे एक सरल रेखा में एक खास क्रम में व्यवस्थित किए गए बिंदुओं के एक समूह के रूप में कल्पित किया जा सकता है। एक गणितीय रेखा की लंबाई अनंत होती है और साथ ही साथ परस्पर विरोधी दिशाओं में भी अनंत होती है, लेकिन उसका मध्य हमेशा मूल, या शून्य पर होता है। एक संख्या रेखा विद्यार्थियों को ऋणात्मक संख्याएं समझने और उन्हें जोड़ना और घटाना आरंभ करने में मदद कर सकती है।

चित्र 1 एक संख्या रेखा।

एक संख्या रेखा इतनी उपयोगी हो सकती है कि गणित सिखाने वाली किसी कक्षा में समान अंतरों पर विभाजित एक लंबी रेखा को बनाना और दर्शाना एक अच्छा विचार हो सकता है, जैसा कि चित्र 2 में दिखाया गया है

चित्र 2 एक खाली संख्या रेखा

रेखा को इस प्रकार बनाना कि उसके द्वारा दर्शाई गई संख्याएं लिखी जा सकें या अलग से नत्थी की जा सकें, इसका अर्थ होगा कि उसका उपयोग संख्या प्रणाली के किसी भी हिस्से के बारे में सोचने के लिए किया जा सकता है। फिर प्रत्येक खंड दर्शाएगा:

• इकाई, दहाई या सैकड़ा आदि।
• अंश या दशमलव, बहुत छोटे दशमलव सहित
• मानक प्रारूप

– और बहुत से अन्य गणितीय विचार।

एक बार विद्यार्थी दीवार पर या अपनी डेस्क पर एक संख्या रेखा देखने के आदी हो गए, तो वे अपने तर्क की जांच के लिए उस रेखा की कल्पना कर सकेंगे।

ऋणात्मक संख्या की धारणा का अस्तित्व केवल शून्य को मूल के रूप में उपयोग करके धनात्मक संख्याओं के सापेक्ष ही होता है। अर्थात, संख्या रेखा पर एक बिंदु चुन लिया जाता है और उसे शून्य आवंटित कर दिया जाता है ताकि शून्य के एक ओर धनात्मक और दूसरी ओर ऋणात्मक होता है। विद्यार्थियों को विपरीत के मायनों में सोचने में मदद करने के लिए पारंपरिक रूप से एक क्षैतिज रेखा के दाएं हिस्से को धनात्मक संख्याओं को दर्शाने के लिए और बाएं हिस्से को ऋणात्मक संख्याओं को दर्शाने के लिए उपयोग किया जाता है। हालांकि एक उर्ध्वाधर रेखा का उपयोग करना भी एक अच्छा विचार है, जिसमें शून्य के ऊपर की संख्याओं को धनात्मक संख्याओं द्वारा और शून्य के नीचे की संख्याओं को ऋणात्मक संख्या द्वारा दर्शाया जाता है।

चाहे आप क्षैतिज रेखा का उपयोग कर रहे हों या उर्ध्वाधर रेखा का, शून्य को आवंटित किए गए बिंदु को हटाने से विद्यार्थियों को यह समझने में मदद मिल सकती है कि यह बस एक अनंत रेखा का एक हिस्सा है, और ऋणात्मक संख्याओं के अध्यायों में इस हिस्से को माना जाता है क्योंकि शून्य पर ही सबकुछ बदल जाता है।

निम्नलिखित गतिविधि में ब्लैकबोर्ड पर बनाई गई एक संख्या रेखा का उपयोग इस तरह किया जाता है कि उससे विद्यार्थियों को यह समझने में मदद मिले कि ऋणात्मक संख्याओं का उपयोग कैसे किया जाना चाहिए और उन संख्याओं को जोड़ना और घटाना कैसे चाहिए। इस गतिविधि में अभिव्यक्ति ‘कल्पना करें यदि...’ का भी उपयोग किया जाता है। इस अभिव्यक्ति से विद्यार्थियों को अपनी कल्पना का उपयोग करने में मदद मिलती है और वे इस विश्वास की सीमा में नहीं रहते कि गणित केवल ‘सही’ या ‘गलत’ ही हो सकता है। यह जानना गणितीय मॉडलिंग में (जैसे शब्द समस्याओं में) खास तौर पर महत्वपूर्ण होता है जहां एक मॉडल एक कल्पित स्थिति दर्शाता है, जो कि आवश्यक नहीं कि सभी मामलों में वैध हो, या शायद कोई सच्ची वास्तविक जीवन स्थिति भी प्रतिबिंबित न करती हो (ब्रूनर, 1986)।

वीडियो: सीखने के लिए बातचीत

विचार के लिए रुकें आपकी कक्षा में गतिविधि 2 कितने अच्छे ढंग से निष्पादित हुई? विद्यार्थियों से किस प्रकार की प्रतिक्रिया अनपेक्षित थी? क्यों? क्या आपने कार्य में किसी भी तरीके का संशोधन किया? अगर हाँ, तो इसके पीछे आपका क्या कारण था? धनात्मक और ऋणात्मक संख्याएं समझने के बारे में आपके विद्यार्थियों की समझ के बारे में आपने क्या सीखा?

4 जोड़ने और घटाने की प्रक्रिया के अर्थ

जोड़ना और घटाना परस्पर व्युत्क्रम गणितीय विधियां हैं। उदाहरण के लिए:

• 5 + 1 = 6
• 6 – 1 = 5
• 6 – 5 = 1

कुछ शोधकर्ताओं (लिंचविस्की और विलियम्स, 1999; ब्रूनो और मार्टिनॉन, 1999) के अनुसार, घटाने के कौशल विद्यार्थियों को ऋणात्मक संख्याओं की धारणा सीखने में सहायता करते हैं। पूर्णांकों के मामले में जोड़ने और घटाने की प्रक्रियाएं आपस में बदलने योग्य होती हैं। उदाहरण के लिए:

• 3 + 5 = 8 = 3 – (–5)

अगली गतिविधि का उद्देश्य है आपके विद्यार्थियों को धनात्मक और ऋणात्मक संख्याओं की गणना करने में शामिल विचार प्रक्रियाओं पर ध्यान केन्द्रित करने में मदद करना।

गतिविधि 3: धनात्मक और ऋणात्मक संख्याओं को जोड़ना

भाग 1: ऋणात्मक संख्याओं के साथ जोड़ने और घटाने की प्रक्रिया को समझने के लिए ‘काउंटर’ मॉडल का उपयोग करना

इस गतिविधि के लिए आपको काउंटर या दो अलग अलग रंगों में कार्ड के टुकड़ों की आवश्यकता होगी। एक रंग धनात्मक चिह्न और दूसरा रंग ऋणात्मक चिह्न दर्शाएगा। इस गतिविधि का एक महत्वपूर्ण हिस्सा है विद्यार्थियों को ऋणात्मक संख्याओं के साथ जोड़ने और घटाने के बारे में बात करने के लिए प्रेरित करना और उनकी विचार प्रक्रिया को समझाना। जब आप अपना अध्याय नियोजित कर रहे हों, तो आप शायद संसाधन 2, ‘सीखने के लिए चर्चा’ पर एक नज़र डालना चाहें।

अपने विद्यार्थियों को बताएं कि काउंटरों की सारी निम्नलिखित व्यवस्था कुल चार होती है।

चित्र 3 कुल चार होने वाले काउंटरों की विभिन्न व्यवस्थाएं।

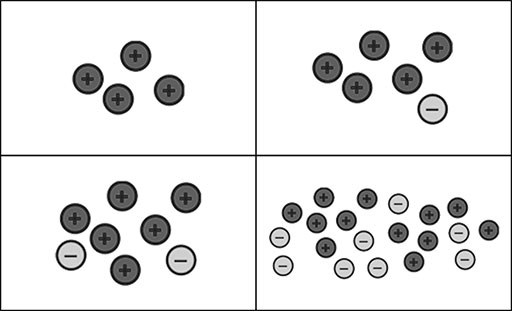
• विद्यार्थियों से कोई अन्य संभावनाएं सुझाने को कहें।
• फिर उनसे यह समझाने को कहें कि ये सारी प्रस्तुतियां 4 कैसे दर्शाती हैं।
• अब -2 को बहुत से अलग अलग तरीकों में दर्शाने के लिए धनात्मक और ऋणात्मक काउंटरों का उपयोग करें, आरंभ केवल दो ‘ऋणात्मक’ काउंटरों से करें। विद्यार्थियों से उनके अपने सुझाव देने को कहना न भूलें
• क्या वे यह समझा सकते हैं कि सारी अलग अलग प्रस्तुतियां -2 क्यों दर्शाती हैं?

भाग 2: छोटे समूहों में, बड़ी संख्याओं के लिए ‘काउंटर’ मॉडल का उपयोग करना

अपने विद्यार्थियों को छोटे समूहों में रखें और उनसे कहें:

• काउंटर या रंगीन कागज़ के टुकड़ों का उपयोग करके, दस से कम कोई संख्या चुनें और धनात्मक और ऋणात्मक काउंटरों की मदद से उस संख्या की कम से कम चार प्रस्तुतियां बनाएं।
• अपनी प्रस्तुतियों को अतिरिक्त सवालों के रूप में दर्ज करें।
• एक ऋणात्मक संख्या चुनें और इसे दोहराएं।
• यदि आपके पास समय है, तो एक और संख्या चुनें जो आपको लगता है आपके लिए कठिन होगी।
• अपनी प्रत्येक प्रस्तुति के लिए सवाल लिखें।

• उन्हें चिह्नित करने के लिए दूसरे समूह के साथ उन्हें बदलें।

यदि आप कर सकें, तो NRICH वेबसाइट पर जा कर धनात्मक और ऋणात्मक काउंटरों के उपयोग के उपाय विकसित करने के कई ओर तरीके खोजें

(स्रोत: भाग 1 NRICH, अदिनांकित से गृहीत।)

वीडियो: स्थानीय संसाधनों का उपयोग करते हुए

विचार के लिए रुकें केस–स्टडी में श्रीमती नागराजु ने सारी कक्षा से एक सवाल पूछा सारे संयोजनों को एक साथ रखने के लिए किस चिह्न की आवश्यकता थी। सही जवाब दिया गया, लेकिन क्या आपको लगता है कि वह सुनिश्चित हो सकता हैं कि यह बिंदु सभी विद्यार्थियों को पूरी तरह समझ में आ गया था? उन्होंने और कौन सी कार्यनीतियां उपयोग में लाई होंगी यह सुनिश्चित करने के लिए कि सारे विद्यार्थी उत्तर के बारे में सोचने और उस पर चर्चा करने में शामिल थे? अब निम्नलिखित प्रश्नों के बारे में सोचें: जब आपने गतिविधि 3 पूरी की, तो आपने अपने विद्यार्थियों की समझ को ताड़ने के लिए कौन से प्रश्न पूछे? क्या किसी भी समय आपको ऐसा लगा कि हस्तक्षेप करना चाहिए? क्या कुछ ऐसे बिंदु थे जिन्हें आपको लगता है कि आपके कुछ या सभी विद्यार्थियों को अपनी समझ को बेहतर बनाने के लिए एक बार फिर देखना चाहिए?

5 सारांश

इस इकाई में ऋणात्मक संख्याओं, उनकी आवश्यकता की समझ और उनके साथ कैसे काम किया जा सकता है, इस पर पूरा ध्यान दिया गया है। इस इकाई को पढ़ कर आपने यह सोचा कि आपके विद्यार्थियों को ऋणात्मक संख्याएं असल में क्या होती हैं यह कल्पना करने के तरीके और उन्हें ऋणात्मक संख्याओं के साथ धन और ऋण देखने के तरीके विकसित करने में कैसे सक्षम करें। आप अपने विद्यार्थियों की कल्पना को उड़ान देने के लिए अभिव्यक्ति ‘कल्पना करें यदि...’ का भी उपयोग कर सकते हैं।

यदि विद्यार्थियों को ऋणात्मक संख्याओं को दुनिया में गणित के उपयोग के सामान्य भाग के रूप में देखना है तो उनके पास ऋणात्मक संख्याओं के साथ काम करने का समृद्ध और विविध अनुभव होना चाहिए। इस इकाई की गतिविधियों में ऋणात्मक संख्याओं को अनुभव करने और उन्हें समझने के लिए विद्यार्थियों को कई अलग अलग तरीके बताए गए हैं।

आपने यह भी देखा है कि कैसे सीखने पर और सीखा कैसे जाता है इस पर विचार करना शिक्षण में बेहतर होने के लिए महत्वपूर्ण है।

संसाधन

संसाधन 1: एनसीएफ/एनसीएफटीई शिक्षण आवश्यकताएँ

यह यूनिट NCF (2005) तथा NCFTE (2009) की निम्न शिक्षण आवश्यकताओं से जोड़ता है तथा उन आवश्यकताओं को पूरा करने में आपकी मदद करेगा:

• शिक्षार्थियों को उनके शिक्षण में सक्रिय प्रतिभागी के रूप में देखें न कि सिर्फ ज्ञान प्राप्त करने वाले के रूप में; ज्ञान निर्माण के लिए उनकी क्षमताओं को कैसे प्रोत्साहित करें; रटने वाली पद्धतियों से शिक्षण को दूर कैसे ले जाएँ।
• विद्यार्थियों को गणित को किसी ऐसी चीज़ के रूप में लेने दें जिसके बारे में वे बात करें, जिसके द्वारा संवाद करें, जिसकी आपस में चर्चा करें, जिस पर साथ मिलकर कार्य करें।

संसाधन 2: सीखने के लिए बातचीत

अतिरिक्त संसाधन

• A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
• National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
• National STEM Centre: http://www.nationalstemcentre.org.uk/
• National Numeracy: http://www.nationalnumeracy.org.uk/ home/ index.html
• BBC Bitesize: http://www.bbc.co.uk/ bitesize/
• Khan Academy’s math section: https://www.khanacademy.org/ math
• NRICH: http://nrich.maths.org/ frontpage
• Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
• Teachnology: http://www.teach-nology.com/ worksheets/ math/
• Math Playground’s logic games: http://www.mathplayground.com/ logicgames.html
• Maths is Fun: http://www.mathsisfun.com/
• Coolmath4kids.com: http://www.coolmath4kids.com/
• National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
• AMT-01 Aspects of Teaching Primary School Mathematics, Block 1 (‘Aspects of Teaching Mathematics’), Block 2 (‘Numbers (I)’), Block 3 (‘Numbers (II)’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-amt-01-study-materialbooks.html
• LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 4 (‘On Spatial Learning’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
• Manual of Mathematics Teaching Aids for Primary Schools, published by NCERT: http://www.arvindguptatoys.com/ arvindgupta/ pks-primarymanual.pdf
• Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
• Textbooks developed by the Eklavya Foundation with activity-based teaching mathematics at the primary level: http://www.eklavya.in/ pdfs/ Catalouge/ Eklavya_Catalogue_2012.pdf
• Central Board of Secondary Education’s books and support material (also including List of Hands-on Activities in Mathematics for Classes III to VIII) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm

References

Acknowledgements

अभिस्वीकृतियाँ

तृतीय पक्षों की सामग्रियों और अन्यथा कथित को छोड़कर, यह सामग्री क्रिएटिव कॉमन्स एट्रिब्यूशन-शेयरएलाइक लाइसेंस (http://creativecommons.org/ licenses/ by-sa/ 3.0/ ) के अंतर्गत उपलब्ध कराई गई है। नीचे दी गई सामग्री मालिकाना हक की है तथा इस परियोजना के लिए लाइसेंस के अंतर्गत ही उपयोग की गई है, तथा इसका Creative Commons लाइसेंस से कोई वास्ता नहीं है। इसका अर्थ यह है कि इस सामग्री का उपयोग अननुकूलित रूप से केवल TESS-India परियोजना के भीतर किया जा सकता है और किसी भी बाद के OER संस्करणों में नहीं। इसमें TESS-India, OU और UKAID लोगो का उपयोग भी शामिल है।

इस यूनिट में सामग्री को पुनः प्रस्तुत करने की अनुमति के लिए निम्न स्रोतों का कृतज्ञतापूर्ण आभार:

गतिविधि 3, भाग 1: 'धनात्मक और ऋणात्मक को समझना', http://nrich.maths.org, © 1997–2014 यूनिवर्सिटी ऑफ़ कैम्ब्रिज से गृहीत (Activity 3, Part 1: adapted from ‘Making sense of positives and negatives’, http://nrich.maths.org © 1997–2014 University of Cambridge.

कॉपीराइट के स्वामियों से संपर्क करने का हर प्रयास किया गया है। यदि किसी को अनजाने में अनदेखा कर दिया गया है, तो पहला अवसर मिलते ही प्रकाशकों को आवश्यक व्यवस्थाएं करने में हर्ष होगा।

वीडियो (वीडियो स्टिल्स सहित): भारत भर के उन अध्यापक शिक्षकों, मुख्याध्यापकों, अध्यापकों और विद्यार्थियों के प्रति आभार प्रकट किया जाता है जिन्होंने उत्पादनों में दि ओपन यूनिवर्सिटी के साथ काम किया है।