Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Tuesday, 10 March 2026, 8:11 AM
अमूर्त गणित के लिए संदर्भ तैयार करना : समीकरण
यह इकाई किस बारे में है
समीकरण बनाना, लिखना, पढ़ना और समीकरण हल करना एक महत्वपूर्ण भूमिका अदा करते हैं - न केवल स्कूल के पाठ्यक्रम में, बल्कि गणितीय विचारधारा की प्रक्रिया में भी। समीकरण अन्य विषयों, जैसे विज्ञान, व्यापार व वाणिज्य में भी महत्वपूर्ण होते हैं। विद्यालय के गणित में, समीकरणों को हल करने पर ध्यान केंद्रित किया जाता है और विद्यार्थी अक्सर समीकरण किस बारे में हैं, यह समझे बिना इसे एक यांत्रि क प्रक्रिया मानते हैं। समीकरणों के बारे में विचार करने में समीकरण की विशेषताएँ, वे कैसे बनते हैं और किस चीज़ का प्रतिनिधित्व करते हैं, शामिल किए जा सकते हैं।
इस इकाई में इन उपेक्षित पहलुओं में से कुछ पर, ऐसे तरीके सुझाकर प्रकाश डाला जाएगा, जिनसे आप बीज गणित के समीकरणों और व्यंजकों की ग्राफीय प्रस्तुति से जोड़कर, और अन्तरों व समानता के बीच भेद बताकर समीकरणों को समझने में अपने विद्यार्थियों की मदद कर सकते हैं। ये गतिविधियाँ भ्रांतियों को सामने लाने और उनपर चर्चा करने के तरीके सुझाने के लिए बनाई गई हैं। विद्यार्थियों की इन गणितीय अवधारणाओं की समझ को बेहतर बनाने में मदद के लिए अवधारणा व मानसिक मानचित्रों का उपयोग किया जाता है।
आप इस इकाई में क्या सीख सकते हैं
- आपके विद्यार्थियों के साथ किस प्रकार समीकरणों की संकल्पना तैयार करें और कैसे उस पर विचार करें।
- कुछ विचार कि किस प्रकार आपके विद्यार्थियों को समीकरणों के प्रयोजन को देखने में मदद के लिए संदर्भों का उपयोग करें।
- समीकरणों की गणितीय अवधारणा के बारे में समझ विकसित करने के लिए किस प्रकार संकल्पना मानचित्रों और मानसिक मानचित्रों का उपयोग करें।
इस इकाई का संबंध संसाधन 1 में दी गई एनसीएफ में दी गई एनसीएफ मेकक में (2005) और एनसीएफटीई (2009) शिक्षण आवश्यकताओं से है।
इस अध्याय में उपयोग की गई विशिष्ट गणितीय शब्दावली
किसी गणितीय समीकरण का रुप होता है p(x) = q(x):
- ‘p(x)’ व ‘q(x)’ बीज गणित के व्यंजक होते हैं।
- इस उदाहरण में, ‘p(x)’ बाएँ हाथ की ओर (LHS) का व्यंजक है।
- ‘q(x)’ दाएँ हाथ की ओर (RHS) का व्यंजक है।
- ‘=’ इंगित करता है कि LHS व RHS का मान बराबर है।
- ‘s’ कोई समाधान समुच्चय है, जो किसी दिए गए समीकरण या असमानता समुच्चय को संतुष्ट करने वाले मानों का समुच्चय है। ऐसे समीकरण में बराबर के चिह्न का अर्थ यह है कि समाधान समुच्चय ‘s’ के लिए एक ओर का मान दूसरी ओर के मान के बराबर आता है।
विचार के लिए रुकें
|
1 समीकरण हल करने के नियमों के बारे में सोचने पर
x का कोई संभव (के कोई संभव) मान खोजने के लिए, जब p(x), q(x) के बराबर हो, हमें इस समीकरण p(x) = q(x) को ‘हल’ करना होगा।
कुछ नियम हैं जो कभी-कभी समीकरण हल करने में सहायक होते हैं। इन नियमों को विद्यार्थी याद कर लेते हैं - या आधे-अधूरे या ग़लत याद
करते हैं और इनके उपयोग करने की प्रक्रिया में कई ग़लतियाँ कर बैठते हैं। गतिविधि 1 का भाग 1 विद्यार्थियों को यह सोचने पर मजबूर करने के लिए बनाया गया है कि ये नियम कहाँ से आए और इन्हें क्यों और कब उपयोग किया जा सकता है। भाग 2 का उद्देश्य विद्यार्थियों को विभिन्न प्रकार के समीकरणों का ज्ञान कराना है। यदि विद्यार्थी दूसरे विद्यार्थियों से अपने विचार साझा कर सकें, तो वे अधिक प्रभावी ढंग से सीखते हैं। उन्हें ‘अपने सहपाठी से उसपर चर्चा करो’ कहना एक अच्छी रणनीति है।
इस यूनिट में अपने विद्यार्थियों के साथ गतिविधियों के उपयोग का प्रयास करने के पहले अच्छा होगा कि आप सभी गतिविधियों को पूरी तरह (या आंशिक रूप से) स्वयं करके देखें। यह और भी बेहतर होगा यदि आप इसका प्रयास अपने किसी सहयोगी के साथ करें, क्योंकि जब आप अनुभव पर विचार करेंगे तो आपको मदद मिलेगी। स्वयं प्रयास करने से आपको शिक्षार्थी के अनुभवों के भीतर झांकने का मौका मिलेगा, जो परोक्ष रूप से आपके शिक्षण और एक शिक्षक के रूप में आपके अनुभवों को प्रभावित करेगा। जब आप तैयार हों, तो अपने विद्यार्थियों के साथ गतिविधियों का उपयोग करें। पाठ के बाद, सोचें कि गतिविधि किस तरह हुई और उससे क्या सीख मिली। इससे आपको सीखने वाले विद्यार्थियों पर ध्यान केंद्रित रखने वाला अधिक शैक्षिक वातावरण बनाने में मदद मिलेगी।
गतिविधि 1: समीकरणों के बारे में सीखना
भाग 1: समीकरण हल करने के खेल के नियम
अपने विद्यार्थियों को निम्न बताएँ:
समीकरण हल करते समय कुछ नियम, या सच हैं, जो उपयोगी हो सकते हैं। हो सकता है आप इन्हें पहले से जानते हों। इस गतिविधि का उद्देश्य यह है कि आप बताएँ कि ये नियम कैसे बने और इन्हें क्यो और कैसे उपयोग किया जा सकता है। आपको इन सामान्य कथनों का अर्थ समझाने के लिए इन कथनों पर लागू होने वाले उदाहरण सोच लेना उपयोगी होगा।
निम्न में से कौन से नियमों का उपयोग समीकरण हल करने के लिए हमेशा, कभी-कभी या कभी नहीं किया जा सकता? आपको कैसे पता?
- यदि p(x) = q(x), तो p(x) + c = q(x) + c
- यदि p(x) = q(x), तो p(x) – c = q(x) – c
- यदि p(x) = q(x), तो p(x) .c = q(x) .c
- यदि p(x) = q(x), तो p(x)/c = q(x)/c
- यदि [p(x)]2 = [q(x)]2, तो p(x) = – q(x)
- यदि [p(x)]2 = [q(x)]2, तो p(x) = q(x)
इन नियमों में से प्रत्येक का एक ग्राफ़ बनाएँ और मूल p(x) = q(x) से उनकी तुलना करें। अपने सहपाठी के साथ चर्चा करें कि इन ग्राफ़ में क्या बदला है और क्या समान है।
भाग 2: कोई नहीं एक और अनन्त समाधान
अपने विद्यार्थियों को निम्न बताएँ:
नीचे तीनों प्रश्नों के उत्तरों की तुलना करें। आपके परिणाम भिन्न कैसे हैं? ये किस प्रकार भिन्न हैं?
- यदि 4(x – 8) = 4x – 32, तो x का पता लगाएँ.
- यदि 4(x – 8) = 4x – 30, तो x का पता लगाएँ.
यदि 4(x – 8) = x – 32, तो x का पता लगाएँ.
प्रत्येक समीकरण के LHS व RHS एक ही ग्राफ़ पर बनाकर अपने बीजीय परिणामों को ग्राफ़ के माध्यम से प्रदर्शित कीजिए। आपने क्या देखा?
समीकरण 2x – 3y = 8 को लें। इस समीकरण का एक ग्राफ़ बनाएँ। अब ax + by = c स्वरूप वाले एक और समीकरण का ग्राफ़ बनाएँ, जिससे दोनों समीकरणों में हों:
- समाधानों का समान समुच्चय
- कोई उभयनिष्ठ समाधान नहीं
- केवल एक उभयनिष्ठ समाधान।
समीकरण 2x – 3y = 8 को फिर से लें। अब ax + by = c स्वरूप वाला एक और समीकरण लिखें, जिससे दोनों समीकरणों में हों:
- समाधानों का समान समुच्चय
- कोई उभयनिष्ठ समाधान नहीं
केवल एक उभयनिष्ठ समाधान।
इस गतिविधि के दौरान , अपने विद्यार्थियों को अपने विचारों के बारे में एक दूसरे से बात करने व एक दूसरे की मदद करने को प्रोत्साहित करें।
केस स्टडी 1: श्रीमती राऊल गतिविधि 1 के उपयोग के बारे में बताती हैं
यह एक शिक्षिका की कहानी है , जिसने अपने माध्यमिक कक्षा के विद्यार्थियों के साथ गतिविधि 1 का प्रयास किया।
अगले भाग पर जाने से पहले भाग 1 को कर लेना अच्छा विचार था। भाग 1 में विद्यार्थियों को पहले तो सामान्य कथनों का अर्थ लगाने में परेशानी हुई। कथन का अर्थ क्या था यह समझने के लिए उदाहरणों के उपयोग का संकेत कारगर रहा।
मैंने कक्षा में घूमकर अन्दाज़ा लगाया कि विद्यार्थी गतिविधि के भाग 2 को कैसे हल कर रहे थे। मैंने देखा कि उनके मन में कई भ्रान्तियाँ थीं। मैंने विचार किया कि मैं इससे कैसे निपट सकता हूँ। मैंने एक निर्णय किया: मैंने सबसे उनके समाधान बताने को कहा और उन सभी को ब्लैकबोर्ड पर लिख दिया, चाहे वह सही हों या ग़लत। फिर मैंने पूछा, ‘तुम्हें कैसे पता कि यही सही उत्तर है? किसी सहपाठी से चर्चा करो।’ उनकी अधिकांश ग़लतियाँ समीकरण के परिचालन से संबद्ध थीं। क्योंकि हमने केवल भाग 1 किया था, अत: इसपर अब चर्चा हो सकती थी। फिर भी मैंने देखा कि यद्यपि अब विद्यार्थियों को पता था कि परिचालन के ‘नियम’ ऐसे क्यों होते हैं, उन्हें समीकरण हल करने के परिप्रेक्ष्य में इन्हें पहचानने के लिए कुछ अभ्यास की आवश्यकता है। एक और भ्रान्ति, और जिससे मुझे आश्चर्य हुआ, यह थी कि कई विद्यार्थियों को 4(x – 8) में कोष्ठकों की भूमिका के बारे में पता नहीं था। उन्होंने केवल कोष्ठक को हटाया और 4x – 8 लिख दिया। इसलिए हमने चर्चा की कि कोष्ठक क्यों दिया जाता है और उसका अर्थ क्या है।
ग्राफ़ बनाने से समीकरणों का अर्थ लगाने में बहुत मदद मिली। रेणू ने सबसे पहले पूरा किया, इसलिए मैंने उसे उन दूसरों की मदद करने को कहा जो किसी समाधान को पाने की कोशिश कर रहे थे। उन्हें इस बात से आश्चर्य हुआ कि ग्राफ़ अलग दिखते थे। वे इस बारे में अपनी चर्चा अधिक आत्मविश्वास से कर पाते थे कि तीनों समीकरणों में क्या समान था और क्या असमान।
प्रमुख संसाधन ‘विचारशीलता को प्रोत्साहित करने के लिए प्रश्नों का उपयोग’ व ‘सीखने के लिए बात करें’ भी देखें।
अपने शिक्षण अभ्यास में दिखाना
जब आप अपनी कक्षा के साथ ऐसा कोई अभ्यास करें, तो बाद में बताएं कि क्या ठीक रहा और कहां गड़बड़ हुई। ऐसे सवालों की ओर ध्यान दें जिसमें विद्यार्थियों की रुचि दिखाई दे और वे आगे बढ़ते हुए नजर आएं और वे जिनका स्पष्टीकरण करने की आवश्यकता हो। ऐसे चिंतन से वह ‘स्क्रिप्ट’ मिल जाती है, जिसकी मदद से आप विद्यार्थियों के मन में गणित के प्रति रुचि जगा सकते हैं और उसे मनोरंजक बना सकते हैं। यदि वे कुछ भी समझ नहीं पाते हैं तथा कुछ भी नहीं कर पाते हैं, तो वे शामिल होने में कम रुचि लेंगे। जब भी आप गतिविधियां करें, इस विचार करने वाले अभ्यास का उपयोग करें व कुछ छोटी चीज़ें नोट करें, जैसे श्रीमती राऊल ने किया, कुछ बहुत छोटी चीज़ें जिन से काफी फर्क पड़ा।
विचार के लिए रुकें ऐसे चिंतन को गति देने वाले अच्छे सवाल हैं:
|
यदि आपको इंटरनेट की पहुँच है, तो वहाँ ऑटोग्राफ़ जैसे गणित के ग्राफ़िंग सॉफ़टवेयर हैं। वे आपके विद्यार्थियों की समीकरणों के ग्राफ़ की कल्पना करने में मदद कर सकते हैं।
2 समीकरणों की पारिस्थितिक संकल्पना
जैसी कि हमने पहले चर्चा की, समीकरण, अक्सर विशुद्ध रूप से विचारों की प्रतीकात्मक अभिव्यक्ति होते हैं। विचार लगभग हमेशा ही प्रतीकात्मक बदलाव के जरिये समीकरण का एक समाधान खोजने का होता है। प्रत्येक बदलाव, यदि उसे पारम्परिक रूप से किया जाए, एक समान समीकरण बनाता है, जो पहले समीकरण से अधिक सरल (हल करने में) होता है। समीकरणों की बीज गणितीय संकेत पद्धति को उनके ग्राफ़ीय निरूपण से जोड़कर अधिक अर्थपूर्ण बनाया जा सकता है।
लेकिन यह फिर भी समीकरणों को देखने व हल करने का एक प्रतीकात्मक तरीका है। यह इस अवधारणा पर काम नहीं करता कि प्रत्येक समीकरण को किसी वास्तविक स्थिति के निरूपण, या मॉडल के रूप में देखा जा सकता है।
आप प्रत्येक समीकरण को समझाने के लिए एक कहानी बना सकते हैं। ऐसी कहानियों को विकसित करने पर काम करने से:
- गणित को सजीव बनाएँ
- विद्यार्थियों को किसी परिस्थिति का अर्थ लगाने में काम में आने वाली गणितीय प्रक्रियाओं के बारे में सोचने दें
- विद्यार्थियों को वास्तव में अचर व चर शब्दों के बीच के अंतर के बारे में और यदि वे आपकी कल्पना को बदलने का फैसला करें तो वह संबंध कैसे परिवर्तित होगा, सोचने को कहें।
अगली गतिविधि समीकरणों की पारिस्थितिक संकल्पना हेतु कहानियाँ सोचने का क्रमिक रूप से ज्ञान कराती है। यह आपके विद्यार्थियों को आगे उनके गणितीय अधिगम में अधिक जटिल समस्याओं के लिए तैयार करेगा।
गतिविधि 2: संदर्भ सोचना
भाग 1: कहानी को बदलना
अपने विद्यार्थियों को निम्न बताएँ:
कल्पना कीजिए मोहन ने एक क्विज़ शो में भाग लेकर अपने प्रत्येक सही उत्तर के लिए कुछ धन जीता और नियम यह था कि उसे प्रत्येक सही उत्तर के लिए पिछले प्रश्न से दुगना धन मिलेगा। यदि पाँचवें प्रश्न के पहले वह 30,000 रु जीत चुका था, तो समीकरण 15x = 30,000 बनेगा, जिसमें x वह राशि थी जो उसे पहले प्रश्न का सही उत्तर देने पर मिली थी।
क्या आप कोई दूसरा संदर्भ - दूसरी कहानी सोच सकते हैं, जो समीकरण 15x = 30,000 द्वारा निरूपित की जा सके?
भाग 2: कोई कहानी सोचना
तैयारी
यह महत्वपूर्ण नहीं है कि विद्यार्थियों के उत्तर सही हैं या ग़लत। अपने विद्यार्थियों की गणित को पिरोने के लिए एक रचनात्मक व कल्पनाशील संदर्भ प्रस्तुत करने की क्षमता पर ध्यान केंद्रित कीजिए (और उन्हें प्रोत्साहित कीजिए) और फिर वे उस संदर्भ तक कैसे पहुँचे यह सबके साथ बाँटिए। शुरू करने के लिए एक अच्छा शब्द है ‘कल्पना कीजिए...’
ब्लैकबोर्ड पर समीकरण 2x + 5 = 12 लिखिए।
गतिवधि
अपने विद्यार्थियों से इस समीकरण की पारिस्थितिक संकल्पना के लिए एक शब्द प्रश्न लिखने के लिए अपनी कल्पनाशीलता का उपयोग करने को कहें। उन्हें बाकी की कक्षा के साथ अपने विचार साझा करने को कहें।
भाग 3: समीकरण बनाना और फिर एक कहानी सोचना
तैयारी
यह भाग 1 और 2 के क्रम में है, जो शब्द प्रश्नों की पारिस्थितिक संकल्पना पर केंद्रित है। अब आप अपने विद्यार्थियों से पहले समीकरण बनाने और फिर उनपर ठीक बैठने वाले शब्द प्रश्न सोचने को कहेंगे।
ब्लैकबोर्ड पर तालिका 1 लिखें:
| 2 | 29 | 10.50 | 3/5 |
| x | 3x | 2.5x | 5x/6 |
| 5x – 8 | 34x – 12 | 5.5x + 1.7 | (2/3)x – 4/5 |
| x2 | 2x2 | x2 + 1 | x2 – 2 |
गतिविधि
निम्न नियमों के आधार पर अभिव्यक्तियों का एक संग्रह चुनकर तालिका 1 से एक समीकरण बनाएँ:
एक ही पंक्ति से चुनी गई दो से अधिक अभिव्यक्तियाँ हमेशा जोड़ी जाती हैं और इन्हें हमेशा ‘=’ चिह्न के एक ही ओर होना चाहिए।
भिन्न पंक्तियों की अभिव्यक्तियाँ ‘=’ चिह्न के दोनों ओर होनी चाहिए।
फिर समीकरण को परिभाषित करने वाला एक शब्द प्रश्न बनाएँ।
उदाहरण के लिए, यदि आप पहली पंक्ति से 2 व 10.50 चुनते हैं और दूसरी से 3x व 2.5x, तो आपको मिलेगा:
3x + 2.5x = 2 + 10.50
5.5x = 12.50.
उदाहरण के लिए एक शब्द प्रश्न ऐसा हो सकता है: ‘5.5 सेमी लंबाई व x सेमी चौड़ाई वाले एक आयत का क्षेत्रफल 12.5 सेमी2 है.’
यदि आपके पास बड़े कागज़ हैं, तो अपने विद्यार्थियों से अपने प्रश्न उनपर लिखकर कक्षा में प्रदर्शित करें। विद्यार्थियों को जाकर एक-दूसरे के शब्द प्रश्न पढ़ने को कहें। आप उन्हें अपनी पसंद के शब्द प्रश्न देखकर उनकी प्रतिलिपि बनाकर उन्हें जाँचने और उन्हें लिखने वाले विद्यार्थियों को फीडबैक देने को कह सकते हैं।
अधिक जानकारी के लिए संसाधन 2, ‘कहानी कहना’ पढ़ें।
केस स्टडी 2: गतिविधि 2 के उपयोग का अनुभव श्रीमती मोहंती बताती हैं
शुरुआत में भाग 1 व 2 को करने में बहुत हिचकिचाहट थी, क्योंकि विद्यार्थियों ने कभी इस प्रकार के प्रश्न नहीं बनाए थे। उन्हें काफ़ी प्रबोधन और भरोसा दिलाने की ज़रूरत पड़ी कि उपयुक्त रहने वाली कोई भी कहानी ठीक थी; और यह कि उसका अविश्वसनीय लगना ज़रूरी नहीं था, या यह कि यदि वे अपनी कहानी ‘कल्पना करें कि…’ से शुरू करेंगे, तो इससे मदद मिलेगी। समीकरण 15x = 30,000 के लिए, मीना ने कहा कि यदि 15 चीज़ें खरीदी गई थीं और कुल चुकाया गया मूल्य रु 30,000 था, तो प्रत्येक का मूल्य x होगा। शरद ने सुझाव दिया कि x काम के दिनों की संख्या हो सकती है और रु 30,000 उनसे मिली कमाई।
अब मैंने उन्हें भाग 2 में दिए गए समीकरण पर प्रयास करने को कहा - जो 2x + 5 = 12 था। कोई आगे नहीं बढ़ा। मैंने बिना कुछ कहे केवल प्रतीक्षा करने का निर्णय किया। लगभग 90 सेकंड के बाद, जो पूरे जीवनकाल जितना लंबा अरसा लगा, लेकिन जितना वह था नहीं, रोहित ने बहुत हिचकिचाहट के साथ पूछा कि यदि वह ऑटोरिक्शा से सफर कर रहा था और रु 5 प्रथम किलोमीटर की न्यूनतम राशि थी व प्रत्येक अगले किलोमीटर के लिए रु रु 2 है, तो उसके द्वारा तय की गई दूरी x किमी थी। मीना ने तुरंत कहा कि नहीं, तुम x + 1 किमी चले होगे। अंजू ने उदाहरण प्रस्तुत किया कि खेल के मैदान में बच्चों के दो समूह थे। फिर पाँच च्चे और आ गए और अब बच्चों की कुल संख्या 12 हो गई - समूहों में कितने बच्चे थे? क्योंकि उत्तर 3.5 था, अत: धन पूर्णांकों व अपरिमेय संख्याओं के बीच अंतर के बारे में एक चर्चा हुई, जो रोचक थी।
भाग 3 की चर्चा मुख्यत: यह थी कि वे प्रश्न तो आसान तरीके से बना सकते थे, लेकिन हमेशा ही उसकी व्याख्या कर पाने वाली परिस्थिति नहीं खोज पाते थे।
श्रीमती मोहंती की तरह, हो सकता है आपके विद्यार्थियों को ये गतिविधियाँ अनजान लगें और उन्हें शब्द प्रश्नों पर सोचने के बारे में आत्मविश्वास पैदा करने के लिए अभ्यास की आवश्यकता हो। इस तकनीक का उपयोग गणित के अधिकाधिक प्रकरणों/पाठों में करें, इससे आपके विद्यार्थियों को गणितीय समीकरणों को समझने में मदद मिलेगी।
विचार के लिए रुकें
|
3 विद्यार्थियों को संबंधित चरों के बारे में विचार करने पर प्रेरित करने के लिए चित्रों का उपयोग करना
समीकरण चरों और अचरों को संबद्ध करती हैं। कौन, कौन है यह पहचाने के अलावा, गणित में एक और रोचक प्रश्न यह है कि दिये गये सन्दर्भ में ‘चर’ एक दूसरे को किस सीमा तक सम्बद्ध करते है ? यह समझने में विद्यार्थियों की मदद करने का अच्छा तरीका है, उन्हें चित्र दिखाकर संबद्ध अचरों के बारे में स्वयं उनके विचार बताने को कहना।
अगली गतिविधि में, विद्यार्थियों को चार स्थितियाँ दी जाएँगी। उन्हें वे सभी चर पहचानने हैं, जो वे सोच सकें और फिर वे जोड़े निर्धारित करने हैं, जो संबंद्ध हो सकते हैं।
गतिविधि 3: संबद्ध चर खोजना
तैयारी
इस अभ्यास के लिए कक्षा को छोटे समूहों (दो, तीन या चार लोगों के) में बाँट दें और फिर उन्हें मिलकर काम करने को कहें। यह निर्धारित करें कि आप समूहों का प्रबंधन कैसे करेंगे। पाठ से पहले इसे कर लेना आवश्यक है, जिससे पाठ के दौरान समय बचाया जा सके। नीचे चित्र 1 की छवियों का उपयोग करें या स्वयं अपनी इसी तरह की छवियों का उपयोग करें, उदाहरण के लिए अख़बारों में से।
गतिवधि
अपने विद्यार्थियों को चित्र 1 की चार छवियों को देखने को कहें। प्रत्येक मामले में, उन चरों की सूची बनाएँ, जो छवि से सम्बन्धित कोई भी पहलू दर्शाते हों।

प्रत्येक सूची के लिए, उन चरों की जोड़ियाँ बनाएँ, जो आपके अनुसार संबद्ध हो सकते हैं। इन चरों से बना एक विशिष्ट संदर्भ बनाएँ व उस संदर्भ को एक समीकरण के रूप में प्रस्तुत करें। अपनी कल्पनाशीलता का उपयोग करें!
गतिविधि के अंत में, समूहों को अपने विचार साझा करने और उनका मूल्यांकन करने को कहें।
केस स्टडी 3: गतिविधि 3 के उपयोग का अनुभव श्री भाटिया बताते हैं
मैंने निर्णय किया कि काम चार-चार के समूह में किया जाए। हमने 11 समूह बनाए और प्रत्येक समूह को चित्र देकर विभिन्न चरों को निकालने व समीकरण बनाने को कहा गया।
वे सभी बड़े उत्साह से चित्रों के विभिन्न चरों को निकालकर लाए। बिना किसी प्रबोधन के, वे कुछ हद तक उन्हें पहचान सकते थे, जो उनके हिसाब से संबद्ध थे और जो उन्हें लगता था कि संबद्ध नहीं थे। फिर कुछ समूह अटक गए। वे यह नहीं सोच पाए कि संपर्क कैसे बनाया जाय।
मैं कक्षा में घूम रहा था, पर मैंने इस बिन्दु पर गतिविधि रुकवा दी और कुछ उदाहरण पूछे। मैंने कहा कि कोई छोटा सा विचार भी सबको आगे बढ़ाने वाला हो सकता है।
शोभा और उसका समूह कुछ भून रही महिला के चित्र पर काम कर रहे थे और बोले कि यदि घर में सदस्यों की संख्या ‘y’ है और प्रत्येक सदस्य ‘x’ पूड़ियाँ खाता है तो यदि महिला ने 40 पूरियाँ बनाईं, तो xy = 40। दूसरे समूह से मोना भी उसी चित्र पर काम कर रही थी और काम में ली जा रही सामग्री से संबंधित संदर्भ लेकर आई। उन्होंने निर्णय लिया कि वह महिला पकौड़े बना रही थी। तो यदि उसने ‘x’ किग्रा बेसन व ‘y’ किग्रा आलुओं का उपयोग किया, और यदि बेसन का प्रति किलो मूल्य ‘a’ है और ‘b’ प्रतिकिलो आलू का मूल्य है, तो उसका व्यय होगा ax + by।
मैंने इन दोनों स्वयंसेवकों की प्रशंसा की व देखा कि उनके उदाहरण अन्य समूहों को अपने विचार-विमर्श में आगे बढ़ाने के लिए काफ़ी हैं। कुछ समय के बाद मैंने प्रत्येक समूह को अपने विचारों में से एक पर एक प्रस्तुति बनाने को कहा और हमने कुछ अच्छी प्रस्तुतियाँ देखीं। मैं वास्तव में इस बात से बहुत प्रभावित
हुआ कि विद्यार्थियों ने कितनी आसानी व प्राकृतिक तरीके से एक समीकरण में कई चरों को रखा - यह कुछ ऐसा था, जो मैं उन्हें पाठ्यपुस्तक से पढ़ाने में भी कतरा रहा था।
विचार के लिए रुकें
अपने विद्यार्थियों की समझ का पता लगाने के लिए आपने क्या सवाल किए?
- विद्यार्थियों से किस प्रकार की प्रतिक्रिया अनपेक्षित थी? क्यों?
- क्या आपको लगा कि आपको किसी समय हस्तक्षेप करना होगा? किन बिंदुओं पर आपको लगा कि आपको और समझाना होगा?
इस गतिविधि में आपने अपने विद्यार्थियों की सीखने की क्षमता का मूल्यांकन कैसे किया?
4 संकल्पना मानचित्र व मस्तिष्क मानचित्र
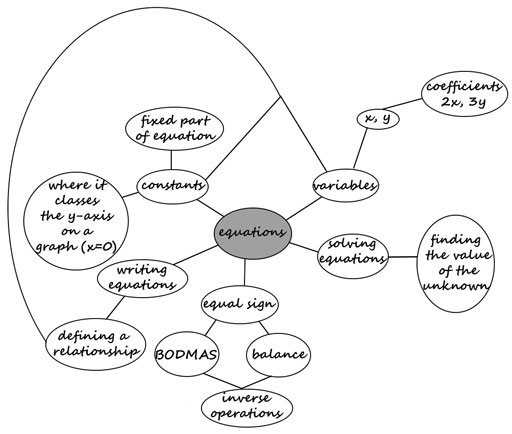
विद्यार्थियों को गणितीय संबंध देखने में सहायता करने वाला एक अच्छा उपकरण है संकल्पना मानचित्र। संकल्पना मानचित्र को किसी विशेष प्रकरण से संबद्ध संकल्पनाओं के बीच के संबंध के बारे में किसी व्यक्ति के ज्ञान का निरूपण माना जा सकता है (नोवाक व गोविन, 1984)। लाक्षणिक रूप से, यह संकल्पना को (एक नोड के रूप में) निरूपित करने वाली शब्दों या वाक्यांशों की एक श्रृंखला और उसे एक अन्य संकल्पना से जोड़कर दोनों के बीच संबंध अभिव्यक्त करने वाली एक रेखा होती है। यह विद्यार्थियों द्वारा अन्वेषण और उनकी समझ की समीक्षा करने के लिए एक अच्छा उपकरण व रणनीति है। इसे विद्यार्थियों के ज्ञान और उनके मन की भ्रांतियों को पता करने के लिए एक आकलन उपकरण के तौर पर भी उपयोग किया जा सकता है। मस्तिष्क मानचित्र संकल्पना मानचत्रि के ही समान होता है, लेकिन मस्तिष्क मानचित्रों का एक केंद्र होता है, जबकि संकल्पना मानचित्र सरल रेखा में हो सकते हैं। इंटरनेट पर संकल्पना व मस्तिष्क मानचित्रों के बहुत से उदाहरण व जानकारी उपलब्ध हैं - मस्तिष्क मानचित्र का एक उदाहरण संसाधन 3 में है।
अगली गतिविधि विद्यार्थियों को अपने सीखने को सुदृढ़ करने के लिए एक संकल्पना मानचित्र बनाने को कहती है।
गतिविधि 4: कोई संकल्पना मानचित्र या मस्तिष्क मानचित्र बनाना
- कक्षा को तीन या चार के छोटे समूहों में बाँट दें।
- ब्लैकबोर्ड पर, ‘समीकरण’ शब्द लिखें और उसके चारों ओर एक वृत्त बना दें।
प्रत्येक समूह से ऐसा कुछ भी सोचने को कहें, जो समीकरणों से सम्बन्धित हो।
उन्हें ऐसी सभी चीज़ों की सूची बनाने को कहें (जितनी अधिक चीज़ें होंगी उतना बेहतर है)।
- एक समूह को उनकी सूची से एक चीज़ पढ़ने को कहें।
- उसे ‘समीकरण’ शब्द से जोड़ते हुए ब्लैकबोर्ड पर लिखें।
- प्रत्येक समूह से एक विद्यार्थी अपना हाथ उठाने को कहें, यदि यह बात उनकी सूची में हो।
उनसे इसे अपनी सूची से हटा देने को कहें।
- जिन समूहों ने इसे नहीं लिखा था, उनसे पूछें कि क्या वे इससे सहमत हैं कि यह ‘समीकरण’ से संबंधित है।
- सभी समूह बारी-बारी शब्द बताते हैं, जिन्हें आप अपने संकल्पना मानचित्र में जोड़ते जाते हैं, इस सावधानी के साथ कि आप शब्दों को समूहीकृत करें व जहाँ उपयुक्त हो, उन्हें रेखाओं से जोड़ दें।
केस स्टडी 4: गतिविधि 4 के उपयोग का अनुभव श्रीमती मेहता बताती हैं
मैं इस गतिविधि से ज़रा डरती थी, क्योंकि मुझे नहीं लगता था कि मैं पूरी तरह समझती थी कि ये संकल्पना मानचित्र किस प्रकार काम करते थे, यद्यपि मैं उन्हें इंटरनेट पर ‘सीखने के लिए संकल्पना मानचित्र’ के माध्यम से खोजा था। जैसा कि सभी वेबसाइटस ने बताया, यह वास्तव में अचछा तरीका है। मैंने सोचा कि मुझे कदम बढ़ाना ही होगा और अपने विद्यार्थियों के साथ इस पर काम करना होगा।
मुझे लगता है यह बहुत अच्छा नहीं हुआ - लेकिन पता लगा कि उन्होंने अन्य विषयों में भी इसका उपयोग किया था (और इस प्रकार इस बारे में मुझसे अधिक जानते थे!)। गणित के शिक्षण के लिहाज से, इसने हमें संबंध जोड़ने और देखने व जटिलता से परिचित होने दिया, जो समीकरणों की जटिलता के ही समान नहीं है।
विचार के लिए रुकें
|
5 सारांश
इस यूनिट में, आपने विभिन्न प्रकार के समीकरणों के बीच समानता व असमानता को समझने के लिए उनके प्रतीकात्मक व ग्राफ़ आधारित निरूपण, दोनों को देखते हुए समीकरणों का अन्वेषण किया। इस यूनिट ने किसी कहानी या चित्र से एक समीकरण बनाने और किसी समीकरण से एक कहानी बनाने के विचार पर भी ध्यान केंद्रित किया। इससे विद्यार्थी यह समझ सकते हैं कि समीकरण विश्व को इस तरह स्वरूपित करते हैं जिससे समाधान खोजे जा सकते हैं। संकल्पना मानचित्रों व मानसिक मानचित्रों के विद्यार्थियों को समीकरणों से संबंधित विचारों पर सोचने में सक्षम बनाने के उपकरण के रूप में उपयोग का भी अन्वेषण किया गया।
इस यूनिट के कई विचार व तकनीकें अन्य प्रकरण पढ़ाते समय भी काम करेंगे। उन दो प्रकरण पर अब एक नोट तैयार करें, जिन्हें आप जल्द ही पढ़ाने वाले हैं, जहाँ थोड़े-बहुत समायोजन के साथ उन अवधारणाओं का उपयोग किया जा सकता है।
संसाधन
संसाधन 1: एनसीएफ/एनसीएफटीई शिक्षण आवश्यकताएँ
इस यूनिट की शिक्षा निम्न NCF (2005) व NCFTE (2009) शिक्षण आवश्यकताओं के संबद्ध है:
- विद्यार्थियों की ज्ञान के निर्माण की क्षमता को प्रोत्साहित करें; सुनिश्चत करें कि सीखना रटने वाले तरीकों से अलग हो; और सीखने को व्यक्तिगत अनुभवों व ज्ञान के आधार पर अर्थ की खोज के तौर पर देखा जाए।
- विद्यार्थी-केंद्रित, गतिविधि आधारित, सहभागिता वाले सीखने के अनुभवों का आयोजन करें।
- गणित को किसी ऐसी चीज़ के रूप में देखें, जिसके बारे में बात की जाए, जिसके द्वारा संवाद करें, जिसकी आपस में चर्चा की जाए, जिसपर साथ मिलकर कार्य किया जाए।
- विद्यार्थियों की अर्थपूर्ण प्रश्न सामने रखने व उनका हल करने में मदद करें।
- विद्यार्थियों को कल्पना द्वारा संबंधों को समझने, संरचना देखने, कारण खोजने, कथनों की सत्यता या उनके गलत होने पर वाद-विवाद में मदद करें।
संसाधन 2: कहानी सुनाना
कहानियां हमारे जीवन को अर्थपूर्ण बनाने में मदद करती हैं। कई पारंपरिक कहानियाँ पीढ़ी-दर-पीढ़ी चली आ रही हैं। वे हमें बचपन में सुनाई गई थीं और इनसे हमें उस समाज के कुछ नियमों और मूल्यों के बारे में पता चलता है, जिसमें हमारा जन्म हुआ है।
कहानियां कक्षा में बहुत शक्तिशाली माध्यम होती हैं: वे:
- रोचक, रोमांचक और प्रेरक हो सकती हैं
- हमें दैनिक जीवन से कल्पना-विश्व में ले जा सकती हैं
- चुनौतीपूर्ण हो सकती हैं
- नए विचारों के बारे में सोचने के लिए प्रेरित कर सकती हैं
- भावनाओं को समझने में मदद करती हैं
- ऐसे सन्दर्भ में समस्याओं को समझने में मदद करती हैं, जो वास्तविकता से अलग होता है और इस कारण कम डरावना होता है।
जब आप कहानियाँ सुनाते हैं, तो विद्यार्थियों से आँखों का संपर्क अवश्य बनाएँ। यदि आप अलग अलग पात्रों के लिए अलग अलग आवाज़ों का उपयोग करेंगे और उदाहरण के लिए उपयुक्त मौकों पर फुसफुसाहट के साथ या ऊँची आवाज़ में बोलकर अपनी आवाज़ का स्तर और लहजा बदलेंगे, तो उनहें इसमें मज़ा आएगा। कहानी की प्रमुख घटनाओं का अभ्यास कीजिए ताकि आप इसे पुस्तक के बिना स्वयं अपने शब्दों में मौखिक रूप से सुना सकें। आप कहानी को जीवंत बनाने के लिए कक्षा में वस्तुएं या कपड़े ला सकते हैं। जब आप किसी कहानी का परिचय देते हैं, तो इसका उद्देश्य अवश्य बताएँ और विद्यार्थियों को इस बारे में सचेत करें कि वे क्या सीख सकते हैं। आपको उन्हें मुख्य शब्दावली का परिचय भी देना पड़ सकता है या कहानी को रेखांकित करने वाली अवधारणाओं के बारे में भी बताना पड़ सकता है। आप विद्यालय में किसी पारंपरिक कथावाचक को भी ला सकते हैं, लेकिन यह अवश्य सुनिश्चित करें कि कथावाचक और विद्यार्थियों, दोनों को अच्छी तरह मालूम हो कि क्या सीखना है।
कथावाचन सुनने के अलावा भी विद्यार्थियों की बहुत सी गतिविधियों का संकेत दे सकता है। विद्यार्थियों से कहानी में उल्लेख किए गए सभी रंगों को नोट करने, चित्र बनाने, मुख्य घटनाओं को याद करने, संवाद तैयार करने या अंत बदलने को कहा जा सकता है। उन्हें समूहों में बाँटा जा सकता है और चित्र या वस्तुएं देकर किसी अन्य नज़रिए से कहानी दोबारा सुनाने को कहा जा सकता है। किसी कहानी का विश्लेषण करके, विद्यार्थियों से कहा जा सकता है कि वे कल्पना और तथ्यों को पहचानें, घटनाओं की वैज्ञानिक व्याख्या पर वाद–विवाद करें या कोई गणितीय समस्याएँ हल करें।
विद्यार्थियों से अपनी स्वयं की कहानियां तैयार करने को कहना एक बहुत शक्तिशाली साधन है। यदि आप उन्हें कार्य को सीमित रखने के लिए संरचना, सामग्री और भाषा देते हैं, तो छात्र आपको अपनी खुद की कहानियाँ बता सकते हैं, यहाँ तक कि गणित और विज्ञान के बहुत कठिन विचारों के बारे में भी। वास्तव में वे विचारों के साथ खेल रहे हैं, अर्थ समझ रहे हैं और अपनी कहानियों के माध्यम से संक्षेप में अवधारणाओं को जान रहे हैं।
संसाधन 3: मस्तिष्क मानचित्र का एक उदाहरण
अतिरिक्त संसाधन
- A newly developed maths portal by the Karnataka government: http://karnatakaeducation.org.in/ KOER/ en/ index.php/ Portal:Mathematics
- Class X maths study material: http://www.zietmysore.org/ stud_mats/ X/ maths.pdf
- National Centre for Excellence in the Teaching of Mathematics: https://www.ncetm.org.uk/
- National STEM Centre: http://www.nationalstemcentre.org.uk/
- OpenLearn: http://www.open.edu/ openlearn/
- BBC Bitesize: http://www.bbc.co.uk/ bitesize/
- Khan Academy’s math section: https://www.khanacademy.org/ math
- NRICH: http://nrich.maths.org/ frontpage
- Mathcelebration: http://www.mathcelebration.com/
- Art of Problem Solving’s resources page: http://www.artofproblemsolving.com/ Resources/ index.php
- Teachnology: http://www.teach-nology.com/ worksheets/ math/
- Maths is Fun: http://www.mathsisfun.com/
- National Council of Educational Research and Training’s textbooks for teaching mathematics and for teacher training of mathematics: http://www.ncert.nic.in/ ncerts/ textbook/ textbook.htm
- AMT-01 Aspects of Teaching Primary School Mathematics, Block 3 (‘Numbers (II)’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-amt-01-study-materialbooks.html
- LMT-01 Learning Mathematics, Block 1 (‘Approaches to Learning’) Block 2 (‘Encouraging Learning in the Classroom’), Block 6 (‘Thinking Mathematically’): http://www.ignou4ublog.com/ 2013/ 06/ ignou-lmt-01-study-materialbooks.html
- Learning Curve and At Right Angles, periodicals about mathematics and its teaching: http://azimpremjifoundation.org/ Foundation_Publications
- Central Board of Secondary Education’s books and support material (also including the Teachers Manual for Formative Assessment – Mathematics (Class IX)) – select ‘CBSE publications’, then ‘Books and support material’: http://cbse.nic.in/ welcome.htm
References
Acknowledgements
अभिस्वीकृतियाँ
तृतीय पक्षों की सामग्रियों और अन्यथा कथित को छोड़कर, यह सामग्री क्रिएटिव कॉमन्स एट्रिब्यूशन-शेयरएलाइक लाइसेंस के अंतर्गत उपलब्ध कराई गई है (http://creativecommons.org/ licenses/ by-sa/ 3.0/)। नीचे दी गई सामग्री मालिकाना हक की है तथा लाइसेंस के अंतर्गत ही इस प्रोजेक्ट में उपयोग की गई है, तथा इसका Creative Commons Licence से कोई वास्ता नहीं है। इसका अर्थ यह है कि यह सामग्री अपरिवर्तित रूप से केवल TESS-India प्रोजेक्ट में ही उपयोग की जा सकती है और यह किसी अनुवर्ती OER संस्करणों में उपयोग नहीं की जा सकती। इसमें TESS-India, OU और UKAID लोगो का उपयोग भी शामिल है।
इस यूनिट में सामग्री को पुनः प्रस्तुत करने की अनुमति के लिए निम्न स्रोतों का कृतज्ञतारूपी आभार किया जाता है:
चित्र 1: ऊपर बाएँ (Figure 1: top left): © Rick212: http://commons.wikimedia.org/ wiki/ File:Australia_vs_India.jpg – यह फ़ाइल Creative Commons Attribution 2.0 Generic लायसेंस; ऊपर दाएँ के तहत लायसेंस प्राप् त है: © Yosarian: http://commons.wikimedia.org/ wiki/ File:Indian_sweet_shop.jpg – यह फ़ाइल Creative Commons Attribution-Share Alike 3.0 अनपोर्टेड लायसेंस; नीचे बाएँ के तहत लायसेंस प्राप् त है: © Sanyambahga http://commons.wikimedia.org/ wiki/ File:Punjabi_woman_in_kitchen.jpg – यह फ़ाइल Creative Commons Attribution-Share Alike 3.0 अनपोर्टेड लायसेंस; नीचे दाएँ के तहत लायसेंस प्राप् त है: © Prattheepps http://commons.wikimedia.org/ wiki/ File:Nilgiri_ooty_railway_station_.JPG.
कॉपीराइट के स्वामियों से संपर्क करने का हर प्रयास किया गया है। यदि किसी को अनजाने में अनदेखा कर दिया गया है, तो पहला अवसर मिलते ही प्रकाशकों को आवश्यक व्यवस्थाएं करने में हर्ष होगा।
वीडियो (वीडियो स्टिल्स सहित): भारत भर के उन अध्यापक शिक्षकों, मुख्याध्यापकों, अध्यापकों और विद्यार्थियों के प्रति आभार प्रकट किया जाता है जिन्होंने उत्पादनों में दि ओपन यूनिवर्सिटी के साथ काम किया है।