Introduction to finite element analysis

Introduction

This free course introduces the finite element method and instils the need for comprehensive evaluation and checking when interpreting results. Engineering is at the heart of modern life. Today, engineers use computers and software in the design and manufacture of most products, processes and systems. Finite element analysis (FEA) is an indispensable software tool in engineering design, and indeed in many other fields of science and technology.

In this course you will be introduced to the essence of FEA; what is it and why do we carry out FEA? As an example of its use, we will look briefly at the case of finite element analysis of the tub of a racing car.

Finally, if you have access to FEA software, you can try out the two exercises where step-by-step instructions are given to help you carry out a simple analysis of a plate and a square beam.

This OpenLearn course is an adapted extract from the Open University course T804 Finite element analysis: basic principles and applications .

Learning outcomes

After studying this course, you should be able to:

• present some basic theory of FEA

• introduce the general procedures that are necessary to carry out an analysis

• present basic information that is necessary for the safe use of FEA.

1 Finite element analysis

In this section we will introduce the finite element method; what it is; its capabilities and who uses it. Later on we will show you a step-by-step example you can follow if you have the use of FEA software.

1.1 What is finite element analysis?

Finite element analysis, utilising the finite element method (FEM), is a product of the digital age, coming to the fore with the advent of digital computers in the 1950s. It follows on from matrix methods and finite difference methods of analysis, which had been developed and used long before this time. It is a computer-based analysis tool for simulating and analysing engineering products and systems. FEA is an extremely potent engineering design utility, but one that should be used with great care. For example, it is possible to integrate a system with computer-aided design software, leading to a type of uninformed push-button analysis in the design process. Unfortunately, colossal errors can be made at the push of a button, as this warning makes clear.

To summarise, the most qualified person to undertake an FEA is someone who could do the analysis without FEA.

Wise words, resisting the temptation to put too much trust in FEA computer applications. If, however, computer-based simulations are set up and used correctly, highly complicated mathematical models can be solved to an extent that is sufficient to provide designers with accurate information about how the products will perform in real life, in terms of being able to carry out or sustain the operating conditions imposed upon them. The simulation models can be changed, modified and adapted to suit the various known or anticipated operating conditions, and solutions can be optimised. Thus, the designers can be confident that the real products should perform efficiently and safely, and can be manufactured profitably. A few more detailed reasons are given below.

The simulations are of continuous field systems subject to external influences whereby a variable, or combination of dependent variables, is described by comprehensive mathematical equations. Examples include:

• stress
• strain
• fluid pressure
• heat transfer
• temperature
• vibration
• sound propagation
• electromagnetic fields
• any coupled interactions of the above.

To be more specific, the FEM can handle problems possessing any or all of the following characteristics.

• Any mathematical or physical problem described by the equations of calculus, e.g. differential, integral, integro-differential or variational equations.
• Boundary value problems (also called equilibrium or steady-state problems); eigenproblems (resonance and stability phenomena); and initial value problems (diffusion, vibration and wave propagation).
• The domain of the problem (e.g. the region of space occupied by the system) may be any geometric shape, in any number of dimensions. Complicated geometries are as straightforward to handle as simple geometries, with the only difference being that the former may require a bit more time and expense. For example, a quite simple geometry would be the shape of a circular cylindrical waveguide for acoustic or electromagnetic waves (fibre optics). A more complicated geometry would be the shape of an automobile chassis, which is perhaps being analysed for the dynamic stresses induced by a rough road surface.
• Physical properties (e.g. density, stiffness, permeability, conductivity) may also vary throughout the system.
• The external influences, generally referred to as loads or loading conditions, may be in any physically meaningful form, e.g. forces, temperatures, etc. The loads are typically applied to the boundary of the system (boundary conditions), to the interior of the system (interior loads) or at the beginning of time (initial conditions).
• Problems may be linear or non-linear.

1.2 Why do finite element analysis?

To get a feeling for some of the more common advantages and capabilities of the FEM, we cite some material from a NAFEMS booklet entitled Why Do Finite Element Analysis? (Baguley and Hose, 1994). NAFEMS, formerly the National Agency for Finite Element Methods and Standards, is an independent and international association for the engineering analysis community and is the authority on all aspects of FEA. In its view, simulation offers many benefits, if used correctly.

The most common advantages include:

• optimised product performance and cost
• reduction of development time
• elimination or reduction of testing
• first-time achievement of required quality
• improved safety
• satisfaction of design codes
• improved information for engineering decision making
• fuller understanding of components allowing more rational design
• satisfaction of legal and contractual requirements.

We should emphasise early on that all FEA models and their solutions are approximate . Their accuracy and validity are highly dependent on understanding the behaviour of the system being modelled, of the modelling assumptions and of the limits input in the first place by the user.

For example, in the field of stress analysis, which is the most common application of FEA for a typical engineering component or body, the general problem in the first place is to determine the various stresses or strains acting at all points in the body, in all directions, for all conditions of loading and use, and for the actual characteristics and properties of the materials of construction. For all but the most simple of shapes and conditions, this task is humanly impossible, hence the need for setting up simulations and modelling the behaviour.

Straight away, we have to make assumptions; these include the following:

• Are the loads worst-case likely or expected scenarios? We have to choose or specify various options of loads and their application points to embrace the likely real situation that the product may experience in use, transport or assembly.
• How is the component held or restrained? In short, what are the boundary conditions and how are these modelled?
• What are the relevant material properties? Do we know, for example, the material behaviour under stress, heat, static or dynamic loading? Is there a reliable database of material properties that we can draw on?

1.3 Capabilities of finite element programs

Finite element codes or programs fall within two main groups:

1. general-purpose systems with large finite element libraries, sophisticated modelling capabilities and a range of analysis types
2. specialised systems for particular applications, e.g. air flow around/over electronic components.

While FEA systems usually offer many analysis areas, the most relevant to this course (and the most commonly used in engineering generally) are linear static structural, linear steady-state thermal, linear dynamic and, to a lesser degree, non-linear static structural. As has been mentioned, quite often, areas of analysis are coupled. For example, a common form of coupled analysis is thermal stress analysis, where the results of a thermal load case are transferred to a stress analysis. Perhaps a loaded component is subject to heat and prevented from expanding because of its physical restraints, which results in a thermally induced strain and consequent stresses within the component.

Some general capabilities of FEA codes for these main areas are summarised in Box 1. These are derived from the NAFEMS booklet by Baguley and Hose (1994). It is advisable to become familiar with these capabilities so that, faced with a particular problem, you will at least have an indication of the required form of analysis. For example, say your problem involved ‘large displacement’. In general, this would indicate that, ultimately, you would need to perform a non-linear analysis. (The meanings of the technical terms in Box 1 will be explained as and when needed in your study of the course.)

1.4 Results of finite element analyses

The amount of information that can be produced by an FEA system, especially for non-linear analysis, is enormous, and, for the first-time user, can be daunting. For the main areas we are considering, most general-purpose finite element codes provide the capability to determine the items in Box 2, again adapted from Baguley and Hose (1994). Results can be presented in various forms such as tabulated numerical data, line graphs, charts and multicoloured contour plots.

It cannot be emphasised strongly enough that while most FEA systems produce vast amounts of data and pretty, highly persuasive pictures, it is the user’s responsibility to ensure correctness and accuracy. They are, in the end, approximate models and solutions, albeit highly sophisticated ones, and it is the user’s responsibility to ensure that results are valid. In the absence of such awareness, the system degenerates into a ‘black box’ category, and the solution it provides will almost certainly be wrong, despite the impressive-looking results.

To summarise: modelling is an important part of modern engineering. FEA is a powerful tool for evaluating a design and for making comparisons between various alternatives. It is not the universal panacea that replaces testing, nor should it allow users to design products without a thorough understanding of the engineering and physical principles involved.

The qualification of assumptions is the key to successful use of FEA in any product design. To achieve this, it is essential to:

• appreciate the physics and engineering inherent in the problem
• understand the mechanics of the materials being modelled
• be aware of the failure modes that the products might encounter
• consider the manufacturing and operating environment of the product and how these might impinge on the performance
• assume that the FEA results are incorrect until they can be verified
• pay close attention to boundary conditions, loads and material models.

Remember that there is an assumption behind every decision, both implicit and explicit, that is made in finite element modelling.

1.5 Basic principles

The basic principles underlying the FEM are relatively simple. Consider a body or engineering component through which the distribution of a field variable, e.g. displacement or stress, is required. Examples could be a component under load, temperatures subject to a heat input, etc. The body, i.e. a one-, two- or three-dimensional solid, is modelled as being hypothetically subdivided into an assembly of small parts called elements – ‘finite elements’. The word ‘finite’ is used to describe the limited, or finite, number of degrees of freedom used to model the behaviour of each element. The elements are assumed to be connected to one another, but only at interconnected joints, known as nodes . It is important to note that the elements are notionally small regions, not separate entities like bricks, and there are no cracks or surfaces between them. (There are systems available that do model materials and structures comprising actual discrete elements such as real masonry bricks, particle mixes, grains of sand, etc., but these are outside the scope of this course.)

The complete set, or assemblage of elements, is known as a mesh . The process of representing a component as an assemblage of finite elements, known as discretisation, is the first of many key steps in understanding the FEM of analysis. An example is illustrated in Figure 1. This is a plate-type component modelled with a number of mostly rectangular(ish) elements with a uniform thickness (into the page or screen) that could be, say, 2 mm.

Figure 1 Example of a mesh over plate component

Show description|Hide description

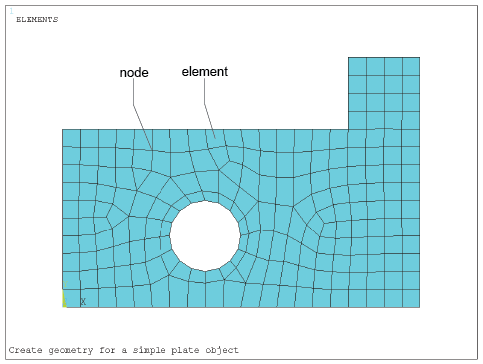
This figure shows a side-on view of a rectangular plate with a hole in it. The hole diameter is about a third of the width of the plate, the width being the shorter of the two rectangular dimensions. At one end of the plate is an extension on one of the long sides. The extension is of square shape and the length of its sides is about one fifth of the longer length of the rectangle. Superimposed on the plate is a mesh of about 220 rectangular elements mostly of square shape, 16 of them on the square extension piece. The elements around and near the hole are somewhat distorted from the ideal square shape.

Figure 1 Example of a mesh over plate component

The field variable, e.g. temperature, is probably described throughout the body by a set of partial differential equations that are impossible to solve mathematically. Instead, we assume that the variable acts through or over each element in a predefined manner – another key step in understanding the method. This assumed variation may be, for example, a constant, a linear, a quadratic or a higher order function distribution. This may seem to be a bit of a liberty, but it can be surprisingly close to reality.

1.6 Outline of the finite element analysis process: structural analysis

The number and type of elements chosen must be such that the variable distribution through the whole body is adequately approximated by the combined elemental representations. For example, if the mesh is too coarse, the resolution of the parametric distribution may be inadequate, whereas too fine a mesh is wasteful of computing time and possibly the user’s time, and in some cases, won’t even solve anyway. Part of the skill will be in designing and refining meshes in areas of high interest or concentration of results variation gradients.

After model discretisation, i.e. subdividing the model domain into discrete elements (the mesh), the governing equations for each element are calculated and then assembled to give system equations. Once the general format of the equations of an element type (e.g. a linear distribution element) is derived, the calculation of the equations for each occurrence of that element in the body is straightforward. Nodal coordinates, material properties and loading conditions of the element are simply substituted into the general format. The individual element equations are assembled into the system equations, which describe the behaviour of the body as a whole. For a static analysis, these generally take the form , where, in structural problems, [ k ] is a square matrix, known as the global stiffness matrix, is the vector of unknown nodal displacements (or temperatures in thermal analysis) and is the vector of applied nodal forces (or heat flux in thermal analysis). The equation is directly comparable to the equilibrium or load–displacement relationship for a simple one-dimensional spring we invoked previously, where a force F produces or results from a deflection u in a spring of stiffness k . To find the displacement caused by a given force, the relationship is ‘inverted’, i.e. u = k ⁻¹ f .

The same approach applies to the FEM using . However, before the equation can be ‘inverted’ and solved for , some form of boundary condition must be applied, as we’ve seen. In stress problems, the body must be restrained from rigid body motion. For thermal problems, the temperature must be defined at one or more nodes. The solution to the equation is not trivial in practice because the number of equations involved tends to be very large. It is not unreasonable to have 250 000 equations, and consequently [ k ] cannot be simply inverted – there is unlikely to be enough computer memory to store all the numbers and data.

Fortunately, as we’ve seen, [ k ] will probably be banded, i.e. terms are grouped about the leading diagonal of the matrix, and more ‘distant’ terms will be zero. Techniques have been developed to take advantage of these features to store and solve the equations efficiently without going through an ‘inversion’ process. Remember that we are generally solving for the nodal displacement values first; it is then a simple matter (using a computer package) to use the displacements to find the strains and then the elemental stresses, via the appropriate Hooke’s law and strain/stress (constitutive) relations.

The major stages in the creation of any finite element model, according to Baguley and Hose (1997), for most types of analysis are:

• selection of analysis type
• idealisation of material properties
• creation of model geometry
• application of supports or constraints
• application of loads
• solution optimisation.

It is extremely important to:

• develop a feel for the behaviour of the structure
• assess the sensitivity of the results to approximations of the various types of data
• develop an overall strategy for the creation of the model
• compare the expected behaviour of the idealised structure with the expected behaviour of the real structure.

For those of us who like pictorial representations, think of the process as shown in Figure 2. Note the estimated proportions of time and effort that are (or should be!) spent in the various phases of preprocessing, solution and post-processing.

Figure 2 Overview of finite element analysis process – structural simulation

Show description|Hide description

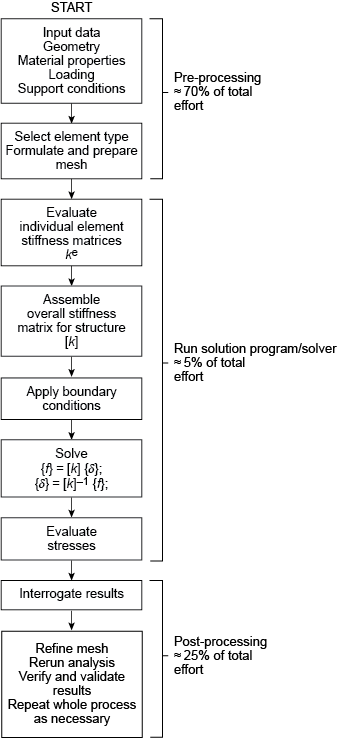
Figure 2 is a vertical block type flow diagram showing the overall process of finite element analysis in a structural application. The first (top) part represents the pre-processing phase comprising about 70 per cent of total effort for an analysis project. This includes: Input data: Geometry, Material properties, Loading, Support conditions; Select element type, Formulate and prepare mesh.

The central portion depicts the actual solving stage, which comprises about 5 per cent the total effort and the steps: Evaluate individual element stiffness matrices; Assemble overall stiffness matrix for structure; Apply boundary conditions; Solve the force displacement matrix equation by inverting the stiffness matrix; Evaluate stresses.

The final post-processing phase comprises about 25 per cent of the total effort and includes the steps: Interrogate results, Refine mesh, Re-run analysis, Verify and validate results, Repeat whole process as necessary.

Figure 2 Overview of finite element analysis process – structural simulation

1.7 Hints and tips on finite element analysis

Don’t rely on one run. Refine the mesh in areas of high stress, repeat two or three times, check the iteration effects.

Remember that we are only ever solving a model of the real problem.

A good finite element model, once set up, is about a 95% accurate solution of the field equations, which themselves are based on a theoretical model, which is idealised from reality, and which uses assumed material properties (Figure 3).

Don’t confuse the processing accuracy of the computer with the validity of the solution.

Computer-aided FEA makes a good engineer better – it makes a bad engineer dangerous !

Figure 3 Reality of the finite element model

Show description|Hide description

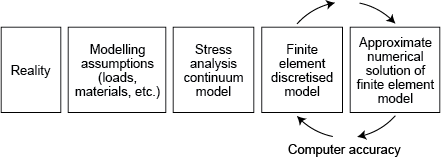
Figure 3 is a horizontal block type flow diagram reminding us of the distance in five steps from reality to the modelling phase. Starting on the left as reality we then have: Modelling assumptions (loads, materials etc.), Stress analysis continuum model, Finite element discretised model, Approximate numerical solution of finite element model. Four curved arrows show the Computer accuracy phase as only the last two blocks.

Figure 3 Reality of the finite element model

1.8 A further few words of caution!

A successful FEA project requires properly executing at least three complex processes according to NAFEMS (2001):

1. The user must be capable and qualified to pose a ‘question’ correctly to the software.
2. The software must be mathematically robust and accurate enough to provide a good solution.
3. The user must again be qualified to understand the results and assess the performance of the system based on these results.

While software vendors have gone to great lengths to make their codes accurate and easy to use, most users aren’t holding up their end by learning the techniques, engineering and discipline required to successfully use these products.

2 Case study

Formula 1 motor racing is a multi-billion dollar, high technology and highly competitive professional sport. In many ways it’s at the leading edge of car design - be it aerodynamics, electronics, materials or engineering. The best drivers compete on a world stage where fractions of a second mean the difference between winning and losing.

Enormous effort goes into the design, manufacture and testing of a racing car and all its components and systems – to gain those fractions of a second. The very latest tools and equipment are used to create the engineering components – usually with a rapid turnaround time and short production cycle. A modern Formula 1 car then is an ideal example to show engineering at its best.

The case study looks at the chassis tub, which not only houses and protects the driver but is the structure to which all the major components are attached.

The clips feature extensive contributions from Lewis Butler, Red Bull’s senior structural analyst, at the time of recording, and Dr Keith Martin of The Open University.

Download this video clip.Video player: Video 1

Show transcript|Hide transcript

Transcript: Video 1

Dr. Keith Martin, The Open University

During this study, we’re going to take a look behind the scenes to see how one team – Red Bull Racing – uses Finite Element Analysis when designing their Formula One cars. Red Bull use the MSC system for all their computer-aided analysis and design, for example, Patran for the pre- and post-processing, and Nastran for the analysis.

For our two case studies, we’re going to look at the design and stress analysis of two parts of the car: the wheel hub in there, and the tub, or chassis.

End transcript: Video 1

Download

Video 1

2.1 Modelling the tub of a Formula 1 racing car

The tub case study uses the same 7 steps approach as the hub case study but some of the steps and aspects are handled differently.

Download this video clip.Video player: Video 2

Show transcript|Hide transcript

Transcript: Video 2

Dr. Keith Martin, The Open University

In this case, we’re looking at the main chassis tub. This is literally the backbone and shell of the car and houses the driver, fuel tank and controls. The front suspension attaches to it. And the whole rear end of the car, engine and all, is attached at the back. Incidentally, the words ‘chassis’, ‘tub’, and indeed ‘chassis tub’ refer to the same part.

End transcript: Video 2

Download

Video 2

Let’s look at more detail on the construction materials of the tub.

Download this video clip.Video player: Video 3

Show transcript|Hide transcript

Transcript: Video 3

Narrator

The tub houses and protects the driver, but is the structure all major components are attached to. As we look at the tub, we can still relate its analysis to the seven-step process we used for the hub. The tub is made of a carbon-fibre composite, sandwiching an aluminium honeycomb core, and is immensely strong, protecting the driver in the event of accidents and impacts.

End transcript: Video 3

Download

Video 3

Here are some more issues affecting the design of the tub.

Download this video clip.Video player: Video 4

Show transcript|Hide transcript

Transcript: Video 4

Dr. Keith Martin, The Open University

Another crucial difference from the hub is that the tub is subject to a range of mandatory safety regulations and tests, which apply to all teams’ cars. Thus, apart from carrying the working loads, there are some additional worst cases in the form of practical tests. Such tests are vital in assessing performance and harnessing data on the properties of the material used, one reason being that the material properties are not quite as easy to determine as are the hub’s steel properties.

End transcript: Video 4

Download

Video 4

Step 1 – The component

As with the hub, we’ll be looking at a specific load case for the tub - one which enables the team to compare new designs or modifications from one model to the next.

Before we can consider building a model of the tub we need to understand what it is – what does it do and how does it interact with other components on the car?

We’ll begin with Lewis describing the component.

Download this video clip.Video player: Video 5

Show transcript|Hide transcript

Transcript: Video 5

Lewis Butler

This is the chassis, which is of carbon fibre composite construction. And this does many jobs. If we go through them in turn, one is to receive all of the suspension loads from the wheels and carry them into the tub, or chassis, and then out into the rest of the car. So the suspension members here you see mounted, they carry all the forces from the wheel into this part. The second of which is to receive loads from impact structures on the front and side of the car. And the third is for a rollover incident where there’s two main areas of the car to try and resist those loads.

There are many regulations we need to try and satisfy, basically, which come in via both impact tests on the front and the side of the car, which is the nose box, which isn’t shown here – but the forces, obviously, are reacted by this component – and the side of the car also adjacent to the driver to give him some protection in a side impact. And the seat belt mountings are obviously in here. And also there are roll hoops, which, again, for the regulations we need to satisfy two load tests, one of which is at the front of the cockpit here.

You can only see this fin here. But there’s actually considerable reinforcement under here to take the forces. Another one up here, which protects his head in a rollover incident, which protects the driver in the event of rolling over. And then between the driver and the rear bulkhead is the fuel cell. And the rear bulkhead is basically where the chassis finishes and the rest of the car begins. And it’s held on just using a handful of fasteners only.

End transcript: Video 5

Download

Video 5

The tub is made from carbon fibre composites. As a cocoon for the driver, it needs to be immensely strong and is subject to a range of impact tests to ensure that it meets the standards stipulated by the governing bodies of Formula 1.

We also know that all the car’s major components such as the engine are mounted directly onto the tub. And that the suspension members carry the forces generated by the wheels into the tub and out into the rest of the car.

Step 2 – The loads

Now the next thing to consider is what load case should we apply to our FEA model.

Download this video clip.Video player: Video 6

Show transcript|Hide transcript

Transcript: Video 6

Lewis Butler

The chassis has many load cases applied to it. The one that we’re going to consider is a pure torsion test, which effectively is applying a pure moment to the front of the car through the suspension, which effectively pushes up on one side and down on the other to give a pure torque, which means there’s a lot of twist going on into the chassis. And the constraint is applied at the rear bulkhead through the fasteners we’ve mentioned before.

End transcript: Video 6

Download

Video 6

There are good reasons for being interested in the torsion test. The torsional stiffness of a racing car chassis is vital in determining overall performance, whatever it is made of.

Download this video clip.Video player: Video 7

Show transcript|Hide transcript

Transcript: Video 7

Dr. Keith Martin, The Open University

The stiffer the chassis, the better the car in terms of handling. The suspension design, operation, and adjustment can be compromised if the chassis isn’t stiff enough. A stiff chassis enables the suspension to work correctly and give the driver confidence in the handling. It’ll be responsive to small adjustments in the setting and tuning of the suspension at the racetrack.

A flexible chassis, on the other hand, will smother or subsume the results of any suspension adjustments predictable when handling on the limit of adhesion and probably spook the driver and be uncompetitive. Another reason is that it’s a non-destructive test and can be easily set up in the workshop. Teams can evaluate their latest chassis design or the results of any modifications in a repeatable manner and thus build up a database of knowledge and performance, which will also be useful in verifying computer models. The actual value of the load in this case is not important. We’re looking at stiffness measured as newton metres torque per degree of twist.

End transcript: Video 7

Download

Video 7

Step 3 – Boundary conditions

The boundary conditions for the tub are quite straightforward. You may recall that the entire back end of the car - comprising the engine, gear box and so on – is attached solidly to the rear bulkhead of the tub. Other bits and pieces such as electrical wiring, controls, and water pipes we can forget about.

Download this video clip.Video player: Video 8

Show transcript|Hide transcript

Transcript: Video 8

Dr. Keith Martin, The Open University

The engine itself forms a structural member. So it’s the front of the engine which bolts firmly to the tub using six threaded fasteners. No rubber anti-vibration mountings on racing cars. The engine, of course, is hugely stiff, almost a solid lump, in fact. Thus, we can say that the chassis tub connects to an infinitely stiff structure at six mounting points.

We say that, under any load condition on the tub, the back end mountings are going nowhere. We assign them a boundary condition restraint of zero displacement in all three directions, x, y, and z. That’s restraining the tub.

The load is applied at the front end as equal and opposite moment arms, a couple in other words, acting through the suspension pick up points. The suspension itself is assumed to be very stiff, no spring resilience for this bit of the exercise. So, the chassis tub experiences a pure torsion due to the applied couple.

End transcript: Video 8

Download

Video 8

Step 4 – Modelling issues and assumptions

For both the boundary condition restraints and load input points we can expect some localised high stresses. We’re not interested in these though. As long as the loads and reaction forces are fed into the structure, the main part - the bit we’re interested in - will be modelled and behave close to the real thing.

For this component Steps 1, 2 and 3 are relatively easy, even easier than for the wheel hub.

Considering modelling issues and assumptions, the tub is large, of a complex shape, and made of a material which is clearly not isotropic. It is ‘orthotropic’.

Download this video clip.Video player: Video 9

Show transcript|Hide transcript

Transcript: Video 9

Lewis Butler

The material properties that we use for the chassis are ordinarily linear again, but the data source for that is slightly different because it’s a bit more of a complex problem and there are many more different types of material. They’re obviously not isotropic. They’re all 2D orthotropic layers which come up to build a 2D orthotropic panel.

And all these have different stiffnesses depending on where they are in the car and how many layers of which material we use. So the constitutive model we use is different to that of an isotropic material. And we tend to use manufacturer’s data for that.

The material properties within the chassis are slightly different. So most of the components in each of the layers is a 2D orthotropic material. So that was a different subset within the model when you apply them. And each of the layers-- because they can be orientated differently to one another – allows you to build up different stiffnesses in different directions. And that makes it more complex, both from getting a hold of the data we require, and also actually validating that against tests. So it’s a little more complicated than isotropic material.

This is the input method that we use in this software for actually representing the material stack with all the different plies. If you see the spreadsheet here, in this case, there are nine different layers. Within that, you specify the thickness of each one and the orientation of each one. And there’s also a core material as well, which, again, is represented using a different kind of constitutive model.

And the clever bit, if you like, is it goes and works out the stiffness of that and the strength of each of those plies individually when you actually apply loads to them. For the load case we’re considering for the chassis, which was a torsion test, which is to try and measure the stiffness of the car under a pure torque. We basically use the suspension components, which you can see is the yellow, the yellow sticks on the screen here. And they’re represented using extremely simplified versions of what is really on the car.

But they still obviously apply the forces in the right positions under the chassis. And from that, the loads are carried in in the correct manner. And we try and do a verification test using this very same loading method.

And we also only mesh half of the car, essentially because any asymmetry is fairly minimal in its impact on the overall results. And it saves an awful lot of time for both simplification of the CAD model and also just construction of the model itself. And also many of the load cases are applicable to just a half car, so we tend to only run half the model to save on computing time.

The constraint case we have here is a little more complicated than just symmetry. It doesn’t really represent doing the same thing on both sides, which is what symmetry ordinarily is. It’s actually trying to make the model do the opposite on one side to the other for a vertical load case. So it constrains, out of the six degrees of freedom-- if you count one, two, three for the translational degrees of freedom, and four, five, and six for the rotational ones, this actually constrains one, three, and five. So in effect, it tries to represent anti-symmetry, which is a little complicated to explain in words, but I can show you in the model later on with the display shape.

What it actually means and what it allows and disallows in terms of rotations and displacements at the centre line. It comes out within maybe 2% or 3% of what is known to be the case with a full model. For the load case that we’re considering here, the torsion test, essentially the load is simply a vertical force applied at the contact patch here. And as you can see from there, the load travels up through my representative wheel which is effectively just there for measuring displacement. It’s not applying the load to the suspension members.

Again, these are just representative components, which are very stiff to make sure that the only variable within the model in terms of stiffness comes from the chassis itself, the main body, so that year on year we get good comparison between the effect of that component only within the system. The constraints, at the rear end of the car, are simply the engine mounts, which we showed a little bit earlier on, across the road, on the real component, and you can see there they are just constrained in all three displacement degrees of freedom.

Any calculations that are made on those for strength are done using hand calculations rather than the FE model, so local stresses are ignored. And the final thing is the anti-symmetry constraint on the centre line. So as you can see, this is trying to represent what happens to the overall car by just loading half of it. And to do this, it effectively constrains, of the six degrees of freedom, if one, two, and three were the translational x, y, and z coordinates, and four, five, and six were the rotational x, y, and z, it constrains degree of freedom one, three, and five.

And that is effectively the three that you wouldn’t constrain if you were doing symmetry. It’s the exact opposite, which is why we call it anti-symmetry. And that does fairly accurately represent what happens during this kind of loading.

Dr. Keith Martin, The Open University

Lewis describes it as a 2D orthotropic material. He assumes that it is a homogeneous, linear, elastic material, having two planes of symmetry at every point in terms of mechanical properties, these two planes being perpendicular to each other.

End transcript: Video 9

Download

Video 9

If you compare the chassis tub to the hub, material behaviour is probably the most different aspect. The hub is made of steel, a linear, elastic, homogenous and isotropic material, and can be described using only a couple of numbers.

Download this video clip.Video player: Video 10

Show transcript|Hide transcript

Transcript: Video 10

Narrator

The material of the tub has complicating features. This is due to the directional nature of the plies of carbon fibre set in the material matrix. In addition to this, the plies themselves can be orientated in layers, each layer direction being different

And there is a core material in the centre of the sandwich, having its own set of properties. So instead of entering just a couple of numbers, the orientations and numbers of plies have to be entered and the analysis package will determine the overall stiffness of the laminate, including the core.

Notice the use of symmetry in the model. Only half the tub was modelled. This can save a lot of time and computing resource -- not just the 50% of the missing piece.

If we double the size of a model, it is likely to increase the solver time by something like 10 times. Larger models might not even solve at all. So, using such symmetry shortcuts is a valuable saving. The only complication is the anti-symmetry boundary condition on the cut face. We’ll say a bit more about that during the next step.

End transcript: Video 10

Download

Video 10

Step 5 – Building and solving the FEA model

In this step we must build the model. As it is so large and has complex material properties, we will only build half the model and use symmetry to solve it. A full model may take a very long time to solve, or may not even solve at all.

Download this video clip.Video player: Video 11

Show transcript|Hide transcript

Transcript: Video 11

Lewis Butler

So the next task is to actually mesh the model. And that does take quite a while in this case because you need to make sure that all the elements are joined to one another at any of the geometry interfaces. So here we can see the final mesh, which is relatively fine for the size of the component. And this gives us a reasonable number of elements. I think there’s in excess of 20,000 per half on this model. And obviously that means, with the type of material that we use, that run times are actually a little larger than they would be for an isotropic model.

Before you solve the model, obviously, as always you need to check that the loads you’ve applied are what you expect. So you need to check your resultant forces in the package if it allows you to do so in the pre-processor. And make sure that all your restraints, and again constrain all six degrees of freedom, to stop there being any silly errors during the running.

Assuming that’s the case, you run the model and then look at the results. Now in the case of this component, and for this load case more specifically, we’re not really interested in stresses. Because it is literally just a stiffness check. The loads are all fairly arbitrary, just to allow us to calculate the stiffnesses more easily than normal.

Dr. Keith Martin, The Open University

Remember that Lewis set up the model as one half, considered symmetrical about the car longitudinal centre line. He used so-called quad four elements, which he considered adequate enough for determining overall tub stiffness, not being that interested in local stress gradient details. The trouble is, there were still 20,000 of them, even for just half the model. And what with the complications due to the material properties, significant computing time and resource is needed to solve the model. A model of the complete tub would need vastly more resource.

Notice that although the tub shape itself is symmetrical about the centre plane of the car, an anti-symmetry boundary condition was applied to the surfaces representing the cut between the two halves. This was because the loading on each half was not reflected as with a mirror but was equal and opposite due to the applied couple torsion action. Thus, an anti-symmetry boundary condition was necessary.

End transcript: Video 11

Download

Video 11

Download this video clip.Video player: Video 12

Show transcript|Hide transcript

Transcript: Video 12

Narrator

If we look at the six degrees of freedom for each node on the cut face, the x-axis is aligned with the car longitudinal centre line. The y-axis goes across the car, side to side. The z-axis is vertical.

For the anti-symmetry condition, the x and z directional degrees of freedom are constrained, as is the rotational degree of freedom about the y-axis. If the loading arrangement was also symmetrical, the symmetry boundary condition would be the exact opposite – constrain y displacement, constrain the rotations about the x and z axes.

End transcript: Video 12

Download

Video 12

Step 6 – Post-processing the FEA model

Once it is solved, we go to the post-processing step to view the results of the calculations.

Download this video clip.Video player: Video 13

Show transcript|Hide transcript

Transcript: Video 13

Lewis Butler

As you can see here, we’ve got the display shape of the torsion test. And you can clearly see the movement that effectively means it behaves like a torque tube towards the front of the car where there’s a large amount of rotation going on and very little displacement vertically. And that is, again, a function of the constraint case that we used, which makes the other half of the car think that it’s being loaded in the opposite direction.

And again, you can see that a large amount of the movement comes from having this big hole in the top of the cockpit where, rather inconveniently, the driver needs to go. If it wasn’t for that, we could be a lot, lot stiffer. So that’s obviously the area we concentrate on in terms of stiffening the car to try and meet targets each season.

End transcript: Video 13

Download

Video 13

In this case, Lewis was only interested in the relative stiffness of the chassis tub, particularly any effects due to modifications in the driver area which was the weakest in terms of torsion.

Step 7 – Post testing and verification

The model can be adapted for each new car and any tests go towards verifying the computer model on a continuing basis.

Download this video clip.Video player: Video 14

Show transcript|Hide transcript

Transcript: Video 14

Lewis Butler

The tests that we actually carry out in the FE is representative of what we try and do on the car each season to verify its overall stiffness. And whilst this component isn’t ever tested in isolation in this manner, we know by measuring at different sections along its length how accurate the model is, and if this kind of model, basically with the assumptions that we’ve made doesn’t come out within about 5% of the tested value, then we’d probably flag it up as some kind of problem, and then re-investigate it after that.

Dr. Keith Martin, The Open University

It’s interesting that Red Bull have carried out detailed measurements of real test chassis tubs at various positions along the length-- the best form of verification. Interesting, also, that they’re disappointed if the measured values and computed results are not within 5% of each other. That’s a very satisfactory result, particularly with such a complicated part and with the non-isotropic material properties. Clearly, FEA is a very powerful simulation tool.

End transcript: Video 14

Download

Video 14

The beauty of Red Bull’s approach to this model is that it is quite easy to match up with a real test and compare results.

The model itself has been refined over a few seasons and developed, based on subsequent testing of real tubs. This means the model can be used with confidence. Any improvements in torsional stiffness that it predicts are likely to be real.

Download this video clip.Video player: Video 15

Show transcript|Hide transcript

Transcript: Video 15

Dr. Keith Martin, The Open University

It’s important to consider the results of a finite element analysis with as much rigour as went into the modelling stage. The basic result is the deflection of the structure stored as displacements, ux, uy, and uz, at all the nodes. This is what the solver produces.

Other data are computed directly from these displacements. The displacements are differentiated to produce strains. And then stresses are found using the material properties.

Reaction forces at restraints are computed from the displacements and structural stiffness. Then we have to apply our engineering judgments on these predicted results. We would check for factors of safety and material yield, using perhaps the von Mises equivalent effective stress plots. For potential fatigue life predictions, we may be more interested in principal tensile stress plots. Remember that Red Bull had their own criteria for lifing the components, which would be logged and the components replaced on a regular basis.

End transcript: Video 15

Download

Video 15

The National Agency for Finite Element Methods and Standards (NAFEMS) says that it is a common mistake in computer analysis to assume that the output, or results, of a processing job are as valid as the processing accuracy of the computer.

Instead NAFEMS recommends that it is safest to consider a set of results to be wrong until you are sure that they are at least of the expected orders of magnitude. For example computed reaction forces agree closely with hand calculated values and so on.

Remember, the computer won’t tell you that you’ve modelled the restraints properly, or that the material properties are correct.

Download this video clip.Video player: Video 16

Show transcript|Hide transcript

Transcript: Video 16

Dr. Keith Martin, The Open University

And don’t forget, in real life the engineers are responsible for making sure that variations in manufacturing, handling and transport, fitting on assembly, and use and abuse in service have all reasonably being covered in the worst case analysis. In Red Bull’s Formula One team, they have built up experience and expertise in the practical performance of the hub and the chassis tub and relating these to the simulation models.

End transcript: Video 16

Download

Video 16

3 FEA exercises

Now is a good time to try out the FEA if you have access to FEA software. These exercises are designed to familiarise you with basic software capabilities.

3.1 Exercise: Analysis of a plate with a hole

Interactive step-by-step solution

1. Specify title
   • Specify a title for your project.
2. Define parameters to be used for geometry input
   • HEIGHT = 0.20
   • WIDTH = 0.50
   • RADIUS = 0.10
   • THICK=0.01
3. Set preferences
   • Make sure that Structural Analysis option is enabled.
4. Define element types
   • Choose an 8-node 1PLANE element (PLANE183).
5. Define options for your element types
   • Set the element options so that it behaves as ‘plane stress with thickness’.
   • The thickness of the element should be set to 0.01.
6. Define material properties

   Set material properties to:

   • Young’s modulus: 2.07 × 10 ¹¹
   • Poisson’s ratio: 0.29
7. Create rectangular area
   • Create a rectangular area with

     Width = WIDTH

     Height = HEIGHT

8. Create circular area
   • Create a circular area with centre at (0, 0) and Radius = RADIUS
9. Subtract hole from plate
   • Use Bollean operations to subtract the hole from the rectangle.
10. Mesh the area with a default mesh
    • Choose ‘Triangular elements’ for Shape.
    • Click Mesh.

    In this example we choose to mesh with triangular elements.

    It should look something like this:

    

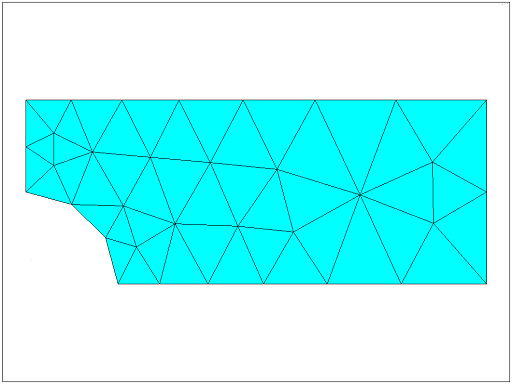    Figure 4 Diagram showing a quarter of the plate with rather large triangular meshing elements

    Show description|Hide description

    The figure shows a coarse meshing of the quarter plate. It is a rectangular shape with a quarter circle cut away from the bottom left corner, representing the quarter of the circular hole. The plate is meshed with about 45 large triangular elements. This represents about seven triangles per long side and three per short side. The triangles are smaller near the cut area.

    Figure 4 Diagram showing a quarter of the plate with rather large triangular meshing elements
11. Apply displacement constraints

    The boundary conditions we apply must represent the symmetric nature of the problem.

    Note: we are going to do this in two distinct steps as an illustration of applying a simple fixed displacement to the nodes attached to a line. In this case, however, as the displacements are equal, i.e. zero, we could have done this in a single step.

    • Apply structural displacement BC to the left edge of the model.
    • Pick UX (x- direction displacement).
    • Enter 0 for Displacement Value.
    • Apply structural displacement BC to the bottom edge of the model.
    • Pick UY (y-direction of the displacement).
    • Enter 0 for Displacement Value.

    Alternative route:

    You can achieve the same result by applying a symmetry boundary condition on left-most and bottom edges.

12. Apply pressure load

    The unit pressure load will be applied to the line at the right.

    • Apply a structural pressure load right-hand edge (line 2).
    • Enter –1.0 for ‘Load Pressure’ value (this ensures that the pressure is outwards as we have a tensile load).
13. Solve
    • Solve the arrangement.
14. Plot the deformed shape
    • The maximum displacement is given as DMX = 0.321 × 10–11. This seems reasonable for a unit load.
15. Plot the element stress in the x direction

    The element stress is a good thing to look at after the displacement. It will show us any steep gradients.

    Note that we have rather steep gradients in the area of concern around the hole.

    We will address this by refining the mesh.

16. Refine mesh

    This command will subdivide all the elements.

    However, in some programs before refining the mesh we need to remove the loads.

    The resultant global refinement is given below. Compare this mesh with the one above.

    

    Figure 5 The same plate as the one shown in Figure 4 but with finer meshing.

    Show description|Hide description

    This figure shows the same plate as in Figure 4, however with much smaller elements. This time there are about 14 triangles per long side and about four per short side. On average the area of each of these elements is about one quarter of the area of elements shown in Figure 4.

    Figure 5 The same plate as the one shown in Figure 4 but with finer meshing.
17. Refine mesh near hole

    You should refine further around the top of the hole.

    • Select the three nodes at the top tip of the circular cut.
    • Refine the mesh in these elements/nodes.

    This produces more elements in the area of interest.

18. Re-introduce loads and Solve

    Repeat steps 11 and 12 above to add load, then solve.

19. Read in the new data set and plot the element stress in the x-direction
    • Choose X-Component of stress to plot.

    The stress contours are now smoother across the element boundaries and the stress legend shows a maximum value of 4.39 Pa. We must check these results. Find the theoretical stress concentration factor, K _t , for this problem in any good source. We determine that for this geometry, K _t = 2.17. The maximum stress is given by:

    ( K _t )(load)/(net cross sectional area)

    Using a pressure of p = 1.0 Pa we get:

    σ _{x, MAX} = 2.17× p ×(0.4)(0.01)/[(0.4-0.2)*0.01] = 4.34

    The computed maximum value is 4.38 Pa which is less than 1% in error, assuming that the value of K _t is exact.

20. Exit the program.

3.2 Exercise: Cantilever beam

Problem description

The problem is a simple cantilever beam. We only give outline instructions for most of this problem. You are required to issue the correct commands, based on your previous experience and the given data.

At the end of this exercise you are asked to use your knowledge in beam theory to calculate the bending stresses and to verify the results of your finite element analysis.

Figure 6 Diagram of a cantilever beam with a rectangular cross-section

Show description|Hide description

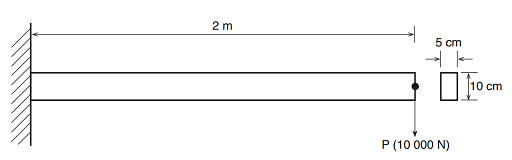
The diagram shows a rectangle representing a slender beam. The length is given as 2 metres and the rectangular cross-section is shown as 10 centimetres thick by 5 centimetres deep. The left side of the rectangle is depicted as being fixed to a wall and at the right-hand side there is a downward facing arrow indicating a force acting on the end of the beam. The value of the force is given as 10000 Newtons.

Figure 6 Diagram of a cantilever beam with a rectangular cross-section

Figure 6 illustrates the problem and associated dimensions. Note that all dimensions should be converted to millimetres and appropriate units for the analysis. Recall that it is the user’s responsibility to insure that all units are consistent! The boundary conditions consist of fully fixing the node on the left.

The applied load is a single point load (force of 10000 N) applied to the right node of the beam. The relevant dimensions are as follows:

Length = 2 m

Depth = 10 cm

Width = 5 cm

The beam is made of steel with a Young’s modulus of 200 GPa and Poisson’s ratio of 0.30.

Interactive step-by-step solution

1. Set title and preferences

   Give your job a title, e.g. ‘Cantilever Beam’.

2. Define element types and options

   Select a 2d elastic beam element.

   Is this a good element choice? You can also look at the options for this element type.

3. Define material properties

   Set Young’s modulus to 2.× 10 ⁵ (in units of N/mm ² ) and Poisson’s ratio to 0.3

4. Define beam section parameters
   • set 50 for width and 100 for height.

   Note that the vertical axis here is the z -axis, so the force will be applied in the z direction.

   It is also a good idea to preview the section data summary to check that all the parameters are entered and calculated correctly.

   The parameters of interest are:

   Area = B × H = 5000

   Second moment of area about y -axis

   = I _yy = B ×( H ³ )/12 = 0.41667× 10 ⁷

5. Create 2 Keypoints

   Create two key points at:

   KP 1 = 0, 0, 0

   KP 2 = 2000, 0, 0

6. Create line

   Create a line between these two key points.

7. Set global element edge size

   Set global element size to 200

8. Mesh the line with a default mesh

   Mesh the line.

9. Apply displacement constraints

   Fix all dofs at key point (or node) number 1

10. Apply force load

    Apply a force of 10000 N in the minus Z direction on the node at the other end of the beam.

11. Rotate the axes

    If necessary, rotate the axes so that the z-axis is pointing up:

12. Solve with default criteria

    Solve the system.

13. Plot deformed shape

    What is the maximum displacement at the tip?

    I got 32.0 mm

14. List nodal displacement values

    Here is the list of displacements I obtained as a function of node x-position:

You can see that the maximum displacement is 32 mm (to 2 dp).

15. List stresses in the beam

    To look at the stresses in the beam we normally need to define an element table. You should read your FEA software’s help menu, particularly on your chosen element to determine the name (or identifier) of variables that give bending stresses.

    I obtained the following values of axial and bending stresses for each element:

16. Validate the bending stresses

    Now you need to use your knowledge in beam theory to verify the results of your FE model. Follow the procedure below:

    1. Draw a free body diagram of your beam and calculate the bending moment at the ends of each element.
    2. Calculate the second moment of area about y-axis, I _yy = B ×( H ³ )/12

    3. Calculate the maximum bending stress at the ends of each element using the classic Engineer’s Bending Equation,

    For example, for element 1 you should get bending stresses of 240 MPa at node I and 216 MPa at node J which gives the average stress of 228 MPa for element 1. This is exactly what we achieved from your finite element model.

17. Exit the program.

Conclusion

In this course you were introduced to the FEA process or method. We outlined the many continuum fields and subjects in which FEA can be applied and showed how modelling using FEA is now an important part of engineering.

This course demonstrated the importance of understanding the limitations and assumptions involved in order to use FEA safely with the aid of some tips and words of caution.

Formula 1 motor racing is at the leading edge of car design – be it aerodynamics, electronics, materials or engineering. The important role that FEA plays in Formula 1 car design is highlighted in a case study involving the tub (body) of a racing car.

Finally, to drive home the importance of practice of FEA, two simple exercises are explained in detail so that, provided you have access to FEA software, you can begin to understand the capabilities of the software.

Today, engineers use computers and software in the design and manufacture of most products, processes and systems. Finite element analysis (FEA) is one of the most important tools in an engineer or designer’s arsenal of digital tools for design and analysis of products and processes. This course has given you a brief introduction to the finite element method and the need for comprehensive evaluation and checking when interpreting results.

References

Acknowledgements

Except for third party materials and otherwise stated (see terms and conditions ), this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence .

Course image: Jonathan Lin in Flickr made available under Creative Commons Attribution-ShareAlike 2.0 Licence .

The material acknowledged below is Proprietary and used under licence (not subject to Creative Commons Licence). Grateful acknowledgement is made to the following sources for permission to reproduce material in this free course:

Every effort has been made to contact copyright owners. If any have been inadvertently overlooked, the publishers will be pleased to make the necessary arrangements at the first opportunity.

Don't miss out

If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University – www.open.edu/ openlearn/ free-courses .